
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Свойствакратного интеграла
Интеграл по области, имеющей нулевую «объемную» меру в
 ,
равен нулю. При этом к областям с нулевой
«объемной» мерой в
,
равен нулю. При этом к областям с нулевой
«объемной» мерой в ,
относятся разнообразные множества,
которые заданы в пространстве
,
относятся разнообразные множества,
которые заданы в пространстве ,
, .
.Если две функции
 и
и интегрируемы в
интегрируемы в ,
то сумма этих функций также интегрируема
в
,
то сумма этих функций также интегрируема
в и
и .
.Если функция
 интегрируема в
интегрируема в ,
а
,
а – постоянная величина, то функция
– постоянная величина, то функция
 также интегрируема в
также интегрируема в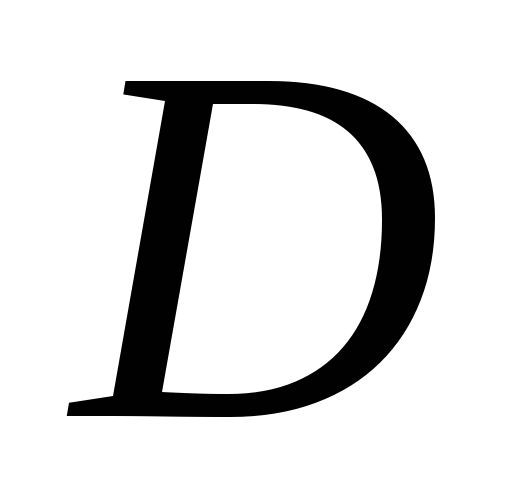 и
и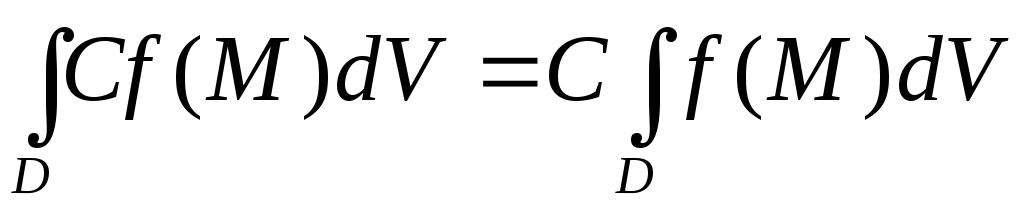 .
.Пусть область
 является объединением областей
является объединением областей и
и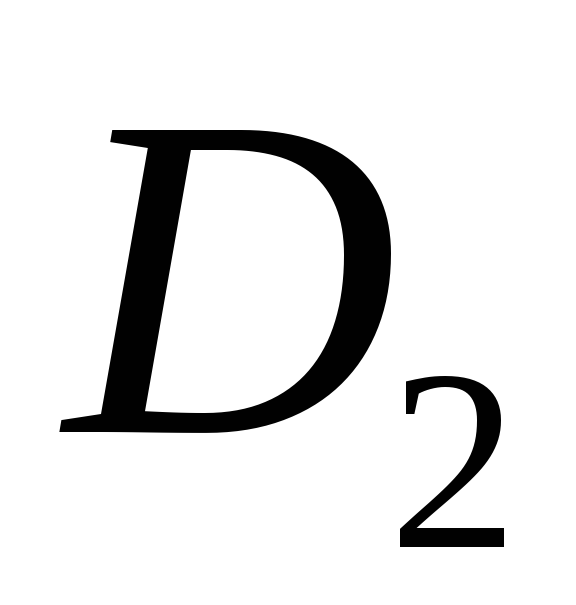 ,
а пересечение этих областей есть
множество
,
а пересечение этих областей есть
множество ,
размерность которого меньше
,
размерность которого меньше .
Если функция
.
Если функция интегрируема в
интегрируема в ,
то она интегрируема в
,
то она интегрируема в и
и и при этом
и при этом .
.Если функция
 определена и интегрируема в
определена и интегрируема в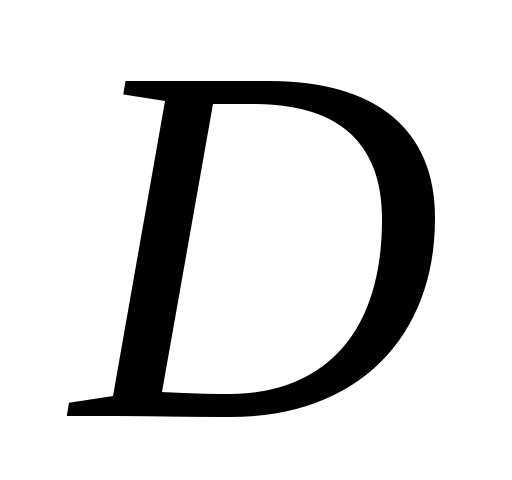 ,
и при этом
,
и при этом (за исключением, быть может, некоторой
части
(за исключением, быть может, некоторой
части с размерностью меньше
с размерностью меньше ),
то
),
то .
.Если две функции
 и
и определены и интегрируемы в
определены и интегрируемы в ,
причем
,
причем
 ,
то
,
то .
.Если функция
 определена и интегрируема в
определена и интегрируема в ,
то
,
то также интегрируема в
также интегрируема в ,
причем
,
причем .
.Если функция
 является постоянной
является постоянной ,
то
,
то .
.Если функция
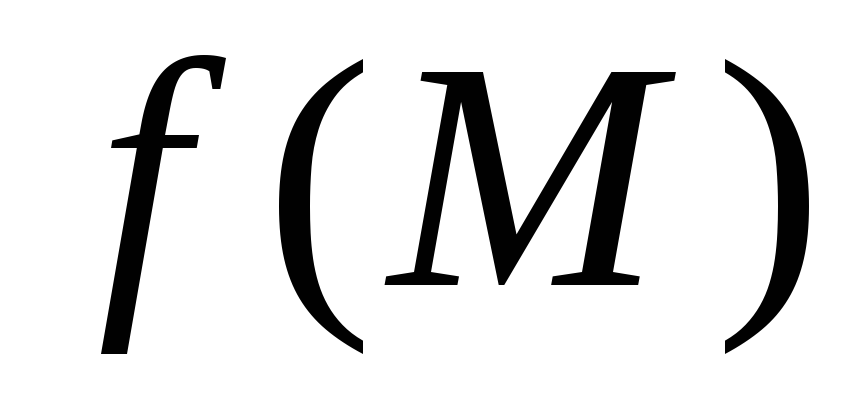 определена и интегрируема в
определена и интегрируема в и ограничена снизу и сверху значениями
и ограничена снизу и сверху значениями и
и ,
соответственно (
,
соответственно ( ,
, ,
,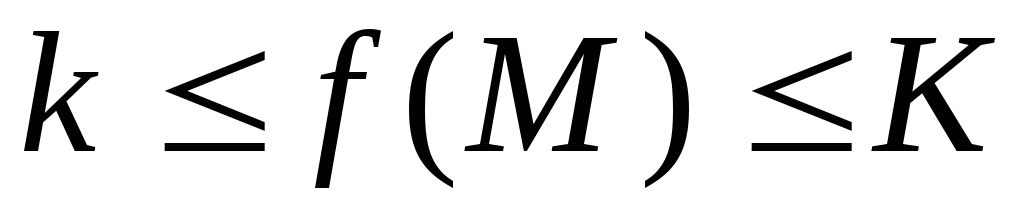
 ),
то
),
то .
.
Контрольные вопросы к теме №10
Понятие двумерных интегральных сумм и их сходимость.
Повторное интегрирование и методы вычисления двойных и кратных интегралов.
Тема 11. Ряды Лекция 22. Ряды
Основные понятия:
числовой ряд; элементы ряда; частная сумма ряда; сходимость ряда; расходящиеся ряды; геометрический ряд; гармонический ряд; остаток ряда; признак Даламбера; интегральный признак; признак Коши; степенной признак; знакопеременный ряд; знакочередующийся ряд; признак Лейбница; абсолютная сходимость ряда; функциональный ряд; область сходимости; равномерная сходимость ряда; степенной ряд; множество сходимости; радиус сходимости; Ряд Тейлора; кусочно-дифференцируемая функция; ортогональные функции; гармонический анализ; коэффициенты Фурье; ряд Фурье.
Основные понятия
Пусть
![]() ‑ последовательность действительных
чисел. Рассмотрим последовательность
‑ последовательность действительных
чисел. Рассмотрим последовательность![]() ,
построенную следующим образом:
,
построенную следующим образом:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
 ;
;
![]()
Последовательность
![]() удобно записывать в виде
удобно записывать в виде![]() .
Такую последовательность называютчисловым рядом. Числа
.
Такую последовательность называютчисловым рядом. Числа![]() называютчленамиилиэлементамиряда. Числовой ряд задают обычно
перечислением его элементов или указанием
формулы, с помощью которой для заданного
называютчленамиилиэлементамиряда. Числовой ряд задают обычно
перечислением его элементов или указанием
формулы, с помощью которой для заданного![]() можно вычислить
можно вычислить![]() -й
член ряда.
-й
член ряда.
Пример.Ряд
![]() имеет
имеет![]() -й
член
-й
член![]() .
.
Поэтому
![]()
т.е.
 .
.
Рассмотрим ряд:
|
|
(1) |
Сумму
 называют
называют
![]() -й
частной суммой ряда(1). Если
последовательность
-й
частной суммой ряда(1). Если
последовательность![]() частных сумм ряда (1) сходится, то ряд
(1) называютсходящимся, а число
частных сумм ряда (1) сходится, то ряд
(1) называютсходящимся, а число![]() называют суммой ряда. Если же
последовательность
называют суммой ряда. Если же
последовательность![]() не имеет конечного предела, то ряд (1)
называютрасходящимся.
не имеет конечного предела, то ряд (1)
называютрасходящимся.
Пример.Рассмотрим ряд
 .Для него
.Для него![]() ,
что представляет собой сумму первых
,
что представляет собой сумму первых![]() членов геометрической прогрессии.
членов геометрической прогрессии.
Если
 ,
то
,
то и
и .
.Если
 ,
то
,
то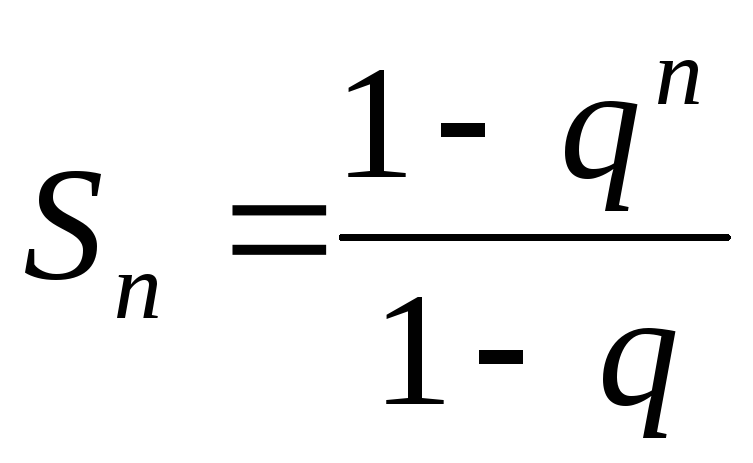 и
и .
.Если
 ,
то
,
то и
и .
.Если
 ,
,
то

и
![]() не существует.
не существует.
Таким
образом, ряд
 при
при![]() сходится и расходится при
сходится и расходится при![]() .
Этот ряд называетсягеометрическим.
.
Этот ряд называетсягеометрическим.
Пусть
ряд (1) сходится и
![]() ‑ его сумма. Поскольку,
‑ его сумма. Поскольку,
|
|
(2) |
то
при
![]() получаем
получаем![]() .
.
Откуда следует необходимое условие сходимости ряда: если ряд сходится, то:
|
|
(3) |
Если условие (3) не выполнено, то ряд расходится.
Пример.Ряд
 расходится, т.к.
расходится, т.к.![]() и
и![]() .
.
Условие
(3) не является достаточным для сходимости
рядя. Даже если оно выполнено, ряд может
расходиться. Покажем это на примере
гармоническогоряда![]() .
Для этого ряда
.
Для этого ряда![]() при
при![]() ,
т.е. условие (3) выполнено. В то же время:
,
т.е. условие (3) выполнено. В то же время:
![]() ,
,
![]() .
.
Поэтому
![]() .
.
Предположим,
что гармонический ряд сходится и
![]() ‑ его сумма, т.е.
‑ его сумма, т.е.![]() при
при![]() .
Поскольку
.
Поскольку![]() ,
то при
,
то при![]() получаем
получаем![]() ‑ противоречие. Значит, предположение
о сходимости гармонического ряда было
неверным.
‑ противоречие. Значит, предположение
о сходимости гармонического ряда было
неверным.
Несколько
первых членов ряда не влияют на его
сходимость. Если у ряда (1) удалить
несколько первых членов, то получим ряд
![]() ,
называемыйостатком ряда(1).
Сходимость ряда равносильна сходимости
его любого остатка.
,
называемыйостатком ряда(1).
Сходимость ряда равносильна сходимости
его любого остатка.
