Формула Тейлора

Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой, является одной из основных задач математического анализа. Для дифференцируемых функций эта задача решается с помощью формулы Тейлора.

Поскольку функция дифференцируема, то ее приращение представимо в виде:

или

_,

т.е. существует многочлен первой степени , такой, что привыполняются условия,.

В более общем виде задачу можно сформулировать следующим образом. Пусть функция определена в некоторой окрестности точки и имеет в этой точкепроизводных,,…,. Необходимо найти многочленстепени не выше, такой, что:

_,

где удовлетворяет условиям:

;

;

;

;

.

Предположим, что искомый аппроксимационный многочлен имеет вид: .

Тогда:

Тогда, с учетом условий (5), можно получить:

Таким образом, если в аппроксимационный полином подставить полученные значения коэффициентов, то полином можно записать следующим образом:

Этот многочлен называется многочленом Тейлора функции . Можно показать, что он удовлетворяет условию. Рассмотрим функцию. Эта функция представляет собой погрешность при замене функциимногочленомв окрестности точки. Из приведенных выше условий следует, что:

.

Для того, чтобы убедиться, что принеобходимо показать, что. Для раскрытия этой неопределенности нужно применитьраз правило Лопиталя:

Полученные выводы можно сформулировать в виде теоремы.

Теорема.Пусть функция определена в некоторой окрестности точкиираз дифференцируема в ней. Тогда, приимеет место формула:

Полученный многочлен называется формулой Тейлора -го порядка с остаточным членом в форме Пеано.

Если , то формула Тейлора называется формулой Маклорена и имеет вид:

Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция имеет производную–го порядка в окрестности точки, то остаточный член может быть представлен в форме Лагранжа:

, .

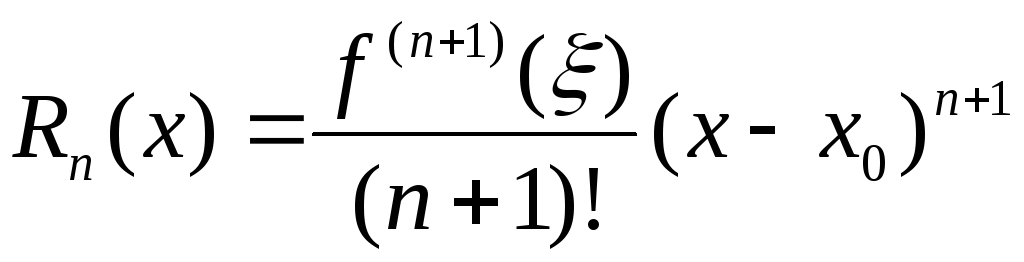Основные разложения

.

.

.

.

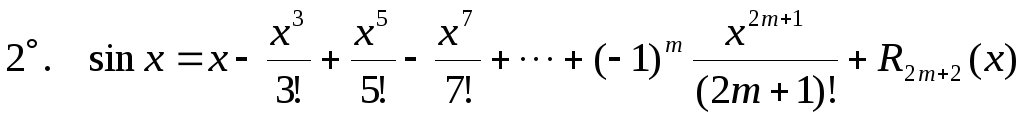В частности, при _:

.

.

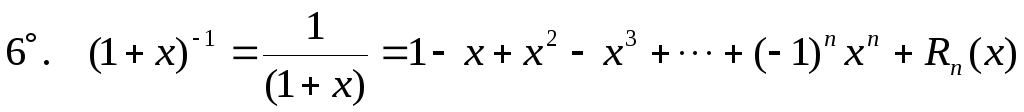Используя основные разложения можно получать формулы Тейлора для других функций. При этом используют то, что:

;

;

;

;

;

.

Понятие об эмпирических формулах

На практике часто возникает задача аппроксимации данных о зависимости между двумя переменными и, полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функциитак, чтобы эта формула наилучшим образом отражала общую тенденцию зависимостиот, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.

Формулы, служащие для аналитического представления опытных данных, называются эмпирическими.Задача нахождения эмпирических формул выполняется в два этапа:

• Установление вида зависимости ;

• Определение неизвестных параметров этой функции.

При определении вида эмпирической функции обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).

Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов, в качестве неизвестных параметров функции выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значенийот значений функции_,вычисленных по соответствующим им значениям аргументов, т.е.:

.

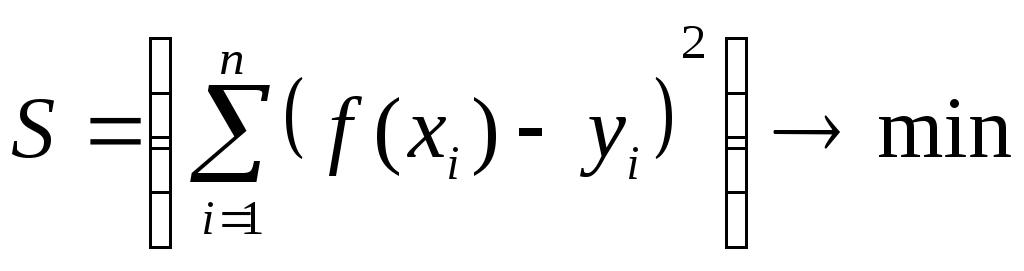Разность называетсяневязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.

В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции возникает необходимость поиска экстремума функции нескольких переменных, поэтому, прежде чем решать эту задачу для конкретных эмпирический функций, необходимо рассмотреть свойства функций нескольких переменных.