
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Бесконечный предел
Наряду
с бесконечно малыми существуют и
бесконечно большие величины, являющиеся
обратными по отношению к бесконечно
малым. Поэтому
 является бесконечно большой (
является бесконечно большой ( ,
при
,
при![]() ),
если
),
если![]()
![]() такое, что при
такое, что при![]()
![]() .
.
Говорят,
что предел последовательности
![]() равен
равен![]() ,
если для
,
если для![]() такое, что
такое, что![]() выполняется неравенство:
выполняется неравенство:![]() .
.
В
отличие от бесконечно малых
последовательностей, бесконечно большие
могут не иметь предела. Например,
![]() по модулю неограниченно растет, но сама
величина
по модулю неограниченно растет, но сама
величина![]() не имеет определенного стремления.
не имеет определенного стремления.
Замечательные пределы
Важную роль на практике играют замечательные пределы, используемые, например, при вычислении пределов функций. Приведем два замечательных предела:
 ,
где
,
где


Покажем,
что
Д ля
простоты примем, что
ля
простоты примем, что
![]() (см. Рис.1.), причем, так как дуга
(см. Рис.1.), причем, так как дуга
![]() стремится к нулю при
стремится к нулю при
![]() ,
то можно считать, что
,
то можно считать, что
 (указанное допущение не является
принципиальным, но позволит использовать
геометрическую интерпретацию). Сравним
величины
(указанное допущение не является
принципиальным, но позволит использовать
геометрическую интерпретацию). Сравним
величины
![]() и
и
![]() с помощью диаграммы, построенной в
первом квадранте.
с помощью диаграммы, построенной в
первом квадранте.
Площади
треугольников
![]() ,
,
![]() и сектора
и сектора
![]() соотносятся следующим образом:
соотносятся следующим образом:

Отсюда
![]() ,
и после деления на
,
и после деления на
![]()
![]() ,
получим
,
получим ,
а для обратных величин
,
а для обратных величин .
Так как при
.
Так как при![]() последовательность
последовательность
![]() ,
а, следовательно,
,
а, следовательно,
![]() ,
то видно, что последовательность
,
то видно, что последовательность
 заключена между двумя последовательностями,
имеющими общий предел, равный 1. Таким
образом, можно сделать вывод, что для
бесконечно малой последовательности
заключена между двумя последовательностями,
имеющими общий предел, равный 1. Таким
образом, можно сделать вывод, что для
бесконечно малой последовательности![]()
![]() ,
справедливо равенство
,
справедливо равенство .
.
При
анализе второго замечательного предела
необходимо показать, что последовательность
 является монотонно возрастающей и
ограниченной сверху. Для этого можно
воспользоваться формулой бинома Ньютона,
положив, что
является монотонно возрастающей и
ограниченной сверху. Для этого можно
воспользоваться формулой бинома Ньютона,
положив, что![]() ,
а
,
а![]() .
Тогда:
.
Тогда:
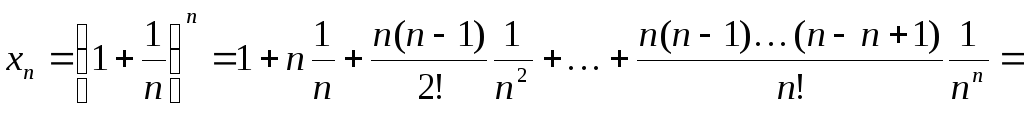
 ,
,

 .
.
Таким
образом,
![]()
![]() ,
так как в каждом слагаемом множители
вида
,
так как в каждом слагаемом множители
вида![]() имеют меньшую величину по сравнению с
имеют меньшую величину по сравнению с при одном и том же
при одном и том же![]() ,
а также выражение для
,
а также выражение для![]() имеет на одно положительное слагаемое
больше.
имеет на одно положительное слагаемое
больше.
Ограниченность
![]() сверху можно показать следующим образом:
сверху можно показать следующим образом:


 .
.
Таким
образом, в соответствии с теоремой о
монотонной последовательности
 имеет предел:
имеет предел:
 ,
,
который
обозначается
![]() (основание натурального логарифма
(основание натурального логарифма![]() ).
).
В высшей математике употребляются почти исключительно натуральные логарифмы, поскольку многие формулы для них оказываются более простыми, чем для логарифмов других систем.
Принцип сходимости
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга.
Лемма
Кантора.Пусть дана последовательность
промежутков
![]() ,
где
,
где![]()
![]()
![]() .
Если при этом
.
Если при этом![]() ,
то последовательности
,
то последовательности![]() и
и![]() имеют равные пределы:
имеют равные пределы:![]() .
.
Теорема Больцано – Вейерштрасса.Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Сходимость
последовательности
![]() к конечному пределу
к конечному пределу![]() означает, что все элементы последовательности
с достаточно большими номерами мало
отличаются от числа
означает, что все элементы последовательности
с достаточно большими номерами мало
отличаются от числа![]() и, следовательно, мало отличаются друг
от друга.
и, следовательно, мало отличаются друг
от друга.
Принцип сходимости формулируют в виде теоремы, называемой критерием Коши.
Критерий
Коши.Последовательность
![]() сходится тогда и только тогда, когда
сходится тогда и только тогда, когда![]()
![]() такое, что
такое, что![]() выполняется неравенство:
выполняется неравенство:![]() .
.
Предел функции. Теорема Гейне
Рассмотрим
функцию
![]() ,
определенную на множестве
,
определенную на множестве![]() .
Пусть
.
Пусть![]() .
Точка
.
Точка![]() называетсяпредельнойилиточкой
сгущениямножества
называетсяпредельнойилиточкой
сгущениямножества![]() ,
если в любой окрестности этой точки
найдутся точки множества, отличные от
,
если в любой окрестности этой точки
найдутся точки множества, отличные от![]() .
В этом случае из множества
.
В этом случае из множества![]() можно выделить последовательность
можно выделить последовательность![]() ,
сходящуюся к
,
сходящуюся к![]() .
К числу предельных точек можно отнести
внутренние точки множества, входящие
в состав
.
К числу предельных точек можно отнести
внутренние точки множества, входящие
в состав![]() вместе с некоторой окрестностью.
Очевидно, что в общем случае точка
сгущения может оказаться не внутренней.
В качестве примера можно привести
множество рациональных чисел
вместе с некоторой окрестностью.
Очевидно, что в общем случае точка
сгущения может оказаться не внутренней.
В качестве примера можно привести
множество рациональных чисел![]() ,
все точки которого в любой окрестности
содержат кроме рациональных чисел и
иррациональные, которые в
,
все точки которого в любой окрестности
содержат кроме рациональных чисел и
иррациональные, которые в![]() не входят.
не входят.
Множество
![]() называется замкнутым, если оно содержит
все свои предельные точки, и множество
называется замкнутым, если оно содержит
все свои предельные точки, и множество![]() называется открытым, если оно состоит
из одних внутренних точек.
называется открытым, если оно состоит
из одних внутренних точек.
Функция
![]() ,
определенная на множестве
,
определенная на множестве![]() имеет предел
имеет предел![]() в точке сгущения
в точке сгущения![]() :
если для любого
:
если для любого![]() найдется такое
найдется такое![]() ,
что при
,
что при![]()
![]()
![]() .
.
Указанное определение опирается на понятие функции и именуется определением предела по Коши.
Существует эквивалентное определение предела, вытекающее из теоремы Гейне.
Эта
теорема сводит понятие предела функции
к пределу сходящихся последовательностей
значений функции
![]() ,
задаваемых для различных последовательностей
,
задаваемых для различных последовательностей![]() ,
стремящихся к
,
стремящихся к![]() .
Можно легко показать, что при любом
выборе последовательности
.
Можно легко показать, что при любом
выборе последовательности![]() ,
если существует предел соответствующих
последовательностей
,
если существует предел соответствующих
последовательностей![]() ,
то этот предел единственен.
,
то этот предел единственен.
Функцию,
имеющую предел не следует путать с
ограниченной функцией. Функция
![]() ,
имеющая предел
,
имеющая предел![]() при
при![]() ,
ограничена в некоторой окрестности
точки
,
ограничена в некоторой окрестности
точки![]() .
Обратное утверждение не верно: ограниченная
функция может не иметь предела.
.
Обратное утверждение не верно: ограниченная
функция может не иметь предела.
Пределы обладают следующими свойствами:
Если
 –
есть постоянная функция, то
–
есть постоянная функция, то ;
;Если существуют
 ,
и в некоторой окрестности точки
,
и в некоторой окрестности точки функция
функция ограничена, т.е.
ограничена, т.е. ,
тогда
,
тогда ;
;Если существуют
 и
и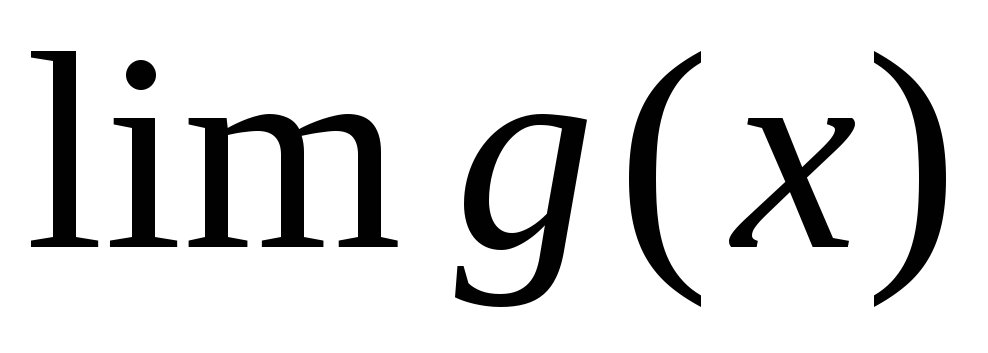 при каком-то условии, то
при каком-то условии, то (при том же условии). Это свойство
справедливо для любого конечного числа
функций;
(при том же условии). Это свойство
справедливо для любого конечного числа
функций;Если существуют
 и
и при каком-то условии, то
при каком-то условии, то (при том же условии). Это свойство также
справедливо для любого конечного числа
функций, в частности, справедлива
формула
(при том же условии). Это свойство также
справедливо для любого конечного числа
функций, в частности, справедлива
формула ;
;Если существуют
 и
и при каком-то условии, то
при каком-то условии, то (при том же условии);
(при том же условии);Если
 и существуют
и существуют ,
, и
и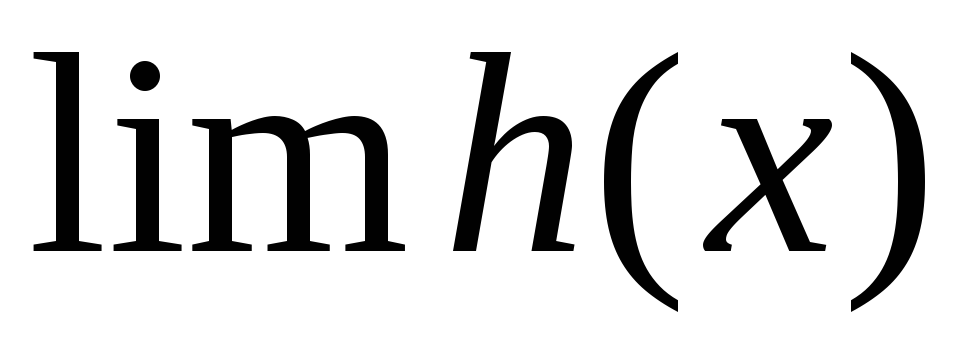 ,
то
,
то .
.
