
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Односторонние пределы
В
определении предела функции предполагалось,
что
![]() произвольным образом. Если при вычислении
предела функции
произвольным образом. Если при вычислении
предела функции![]() при
при![]() считать, что
считать, что![]() ,
то получаютодносторонний предел
справаилиправостороннийпредел
функции в точке
,
то получаютодносторонний предел
справаилиправостороннийпредел
функции в точке![]() .
Если же считать, что
.
Если же считать, что![]() и
и![]() ,
то получают односторонний предел
слеваилилевостороннийпредел.
,
то получают односторонний предел
слеваилилевостороннийпредел.
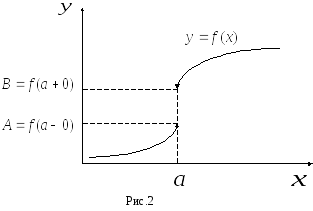
Так,
например, односторонние пределы функции
![]() ,
изображенной на Рис. 2, соответственно,
равны:
,
изображенной на Рис. 2, соответственно,
равны:![]() и
и![]() .
.

Правосторонний
предел обозначают символом
![]() ,
левосторонний ‑ символом
,
левосторонний ‑ символом![]() .
Таким образом:
.
Таким образом:
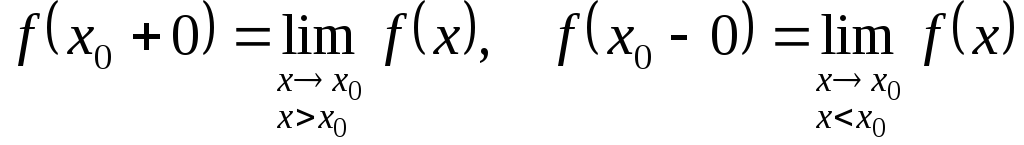 .
.
В
этих определениях предполагается, что
функция определена на некотором
промежутке соответственно справа или
слева от точки сгущения
![]() .
.
Для
того, чтобы у функции
![]() в точке
в точке![]() существовал двусторонний предел
существовал двусторонний предел![]() ,
необходимо и достаточно, чтобы существовали
левосторонний и правосторонний пределы
,
необходимо и достаточно, чтобы существовали
левосторонний и правосторонний пределы![]() и
и![]() функции
функции![]() в точке
в точке![]() ,
и эти пределы были равны между собой:
,
и эти пределы были равны между собой:![]() .
.
Пример.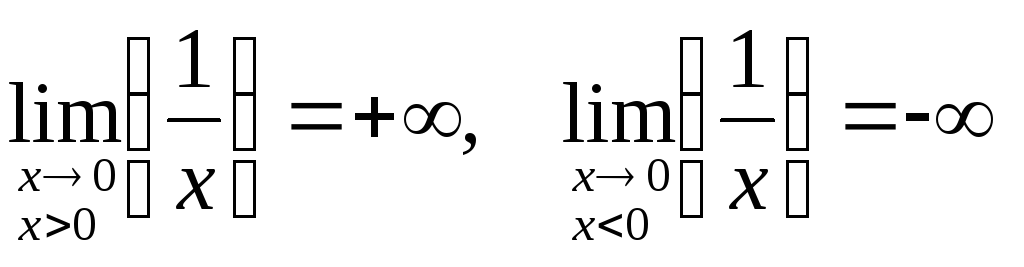
Пример.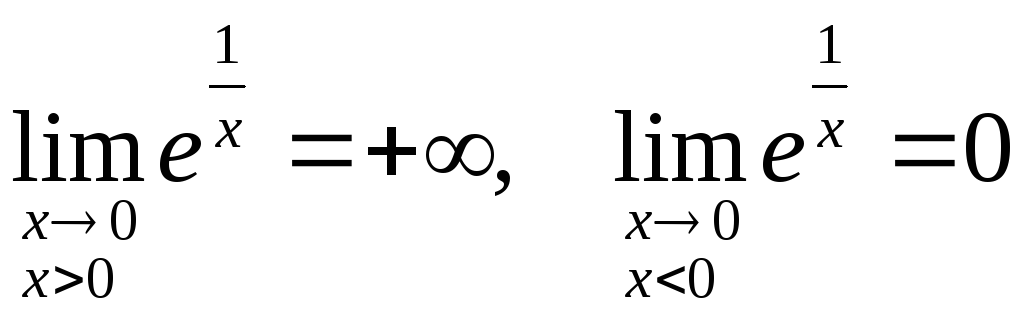
Пределы на бесконечности
Кроме
предела в точке
![]() ,
можно рассматривать предел в точке,
бесконечно удаленной в сторону
,
можно рассматривать предел в точке,
бесконечно удаленной в сторону![]() или
или![]() .
В этом случае понятие предела необходимо
уточнить.
.
В этом случае понятие предела необходимо
уточнить.
Говорят,
что предел функции
![]() при
при![]() равен
равен![]() ,
если для
,
если для![]() существует
существует![]() такое, что для
такое, что для![]() ,
удовлетворяющего условию
,
удовлетворяющего условию![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
Аналогично,
.
Аналогично,![]() при
при![]() ,
если для
,
если для![]() существует
существует![]() такое, что для
такое, что для![]() ,
,![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Если
функция
 ,
где
,
где![]() и
и![]() есть суммы одночленов от переменной
есть суммы одночленов от переменной![]() то предел отношения
то предел отношения![]() при
при![]() или
или![]() равен пределу отношения старших членов
(т.е. членов с наибольшими степенями
переменной
равен пределу отношения старших членов
(т.е. членов с наибольшими степенями
переменной![]() функций
функций![]() и
и![]() ).
).
Пример
3.  ,
поскольку для
,
поскольку для![]() выполнено неравенство
выполнено неравенство ,
если только
,
если только
Пример
4. .
.
Пример 5.
 .
.
Бесконечные пределы
Функция
![]() называетсябесконечно малойпри
называетсябесконечно малойпри![]() (или
(или![]() ,
или
,
или![]() )
если для сколь угодно малого положительного
числа
)
если для сколь угодно малого положительного
числа![]()
![]() найдется такое положительное число
найдется такое положительное число![]() (
(![]() ),
что для всех
),
что для всех![]() будет верно неравенство
будет верно неравенство![]() .
.
При
![]() (
(![]() )
функция
)
функция![]() называетсябесконечно малой,если
для сколь угодно малого положительного
числа
называетсябесконечно малой,если
для сколь угодно малого положительного
числа![]()
![]() найдется такое положительное число
найдется такое положительное число![]()
![]() ,
что для всех
,
что для всех![]() будет верно неравенство
будет верно неравенство![]() .
.
Предел
бесконечно малой величиныв точке
сгущения (или на бесконечности) равен
нулю, т.е.![]() .
.
Теорема:Если функция
![]() ,
определенная на множестве
,
определенная на множестве![]() имеет предел
имеет предел![]() в точке сгущения
в точке сгущения![]() (или на бесконечности), то её можно
представить в виде суммы этого числа и
бесконечно малой величины:
(или на бесконечности), то её можно
представить в виде суммы этого числа и
бесконечно малой величины:![]() .
.
Справедлива
также и обратная теорема:Если
функцию
![]() ,
определенную на множестве
,
определенную на множестве![]() ,
можно представить в точке сгущения
,
можно представить в точке сгущения![]() (или на бесконечности) в виде суммы
числа
(или на бесконечности) в виде суммы
числа![]() и бесконечно малой величины
и бесконечно малой величины![]() :
:![]() то число
то число![]() является пределом этой функции при
указанных условиях.
является пределом этой функции при
указанных условиях.
Свойства бесконечно малых величин:
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;
Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая;
Частное от деления бесконечно малой на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Функция
![]() называетсябесконечно большойпри
называетсябесконечно большойпри![]() (или
(или![]() ,
или
,
или![]() )
если для сколь угодно большого
положительного числа
)
если для сколь угодно большого
положительного числа![]()
![]() найдется такое положительное число
найдется такое положительное число![]() (
(![]() ),
что для всех
),
что для всех![]() будет верно неравенство
будет верно неравенство![]() .
.
При
![]() (
(![]() )
функция
)
функция![]() называетсябесконечно большой,если
для сколь угодно большого положительного
числа
называетсябесконечно большой,если
для сколь угодно большого положительного
числа![]()
![]() найдется такое положительное число
найдется такое положительное число![]()
![]() ,
что для всех
,
что для всех![]() будет верно неравенство
будет верно неравенство![]() .
.
Предел
бесконечно большойвеличиныв
точке сгущения (или на бесконечности)
равен бесконечности, т.е.![]() .
.
Свойства бесконечно больших величин:
Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая;
Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая;
Частное от деления бесконечно большой величины на функцию, имеющую предел в точке
 есть величина бесконечно большая.
есть величина бесконечно большая.
Теорема.Если функция
![]() есть бесконечно малая величина при
есть бесконечно малая величина при![]() (
(![]() )
то функция
)
то функция есть бесконечно большая величина при
есть бесконечно большая величина при![]() (
(![]() ).
).
Обратная
теорема.Если функция
![]() есть бесконечно большая величина при
есть бесконечно большая величина при![]() (
(![]() )
то функция
)
то функция есть бесконечно малая величина при
есть бесконечно малая величина при![]() (
(![]() ).
).
Сравнение бесконечно малых величин:
Две бесконечно малые величины
 и
и называются бесконечно малыми одного
порядка, если предел их отношения есть
конечное число, отличное от нуля, т.е.
называются бесконечно малыми одного
порядка, если предел их отношения есть
конечное число, отличное от нуля, т.е.
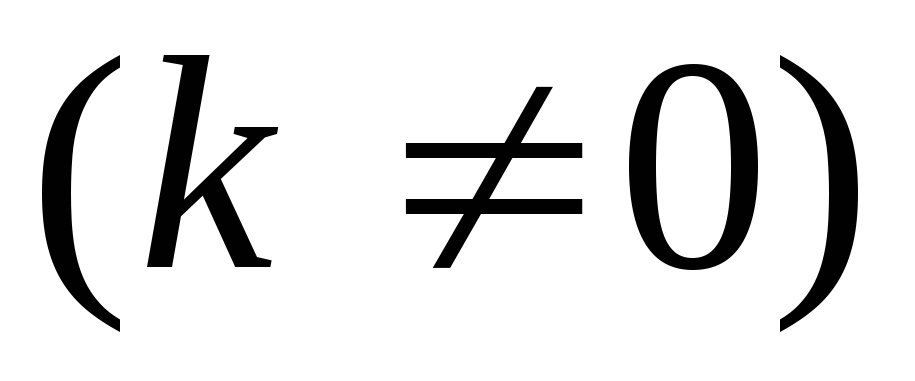 ;
;Величина
 называется бесконечно малой величиной
высшего порядка по сравнению с
называется бесконечно малой величиной
высшего порядка по сравнению с ,
если предел отношения
,
если предел отношения к
к равен нулю, т.е.
равен нулю, т.е. ;
;Величина
 называется бесконечно малой величиной
низшего порядка по сравнению с
называется бесконечно малой величиной
низшего порядка по сравнению с ,
если предел отношения
,
если предел отношения к
к является бесконечно большой величиной,
т.е.
является бесконечно большой величиной,
т.е. ;
;Две бесконечно малые величины
 и
и называются эквивалентными бесконечно
малыми, если предел их отношения равен
единице, т.е.
называются эквивалентными бесконечно
малыми, если предел их отношения равен
единице, т.е. .
.
Пользуясь приведенными выше теоремами, которые устанавливают взаимосвязь между бесконечно малыми и бесконечно большими величинами, можно распространить эти свойства на бесконечно большие величины.
Решение
задачи сравнения бесконечно малых
(бесконечно больших) величин связано с
необходимостью корректно раскрыть
неопределенность
![]() .
Методы раскрытия этой и других
неопределенностей будут подробно
рассмотрены позднее.
.
Методы раскрытия этой и других
неопределенностей будут подробно
рассмотрены позднее.
Если
 и
и![]() ,
,![]() то
то![]()
Если
![]() и
и![]() при
при![]() а
а![]() для
для![]() близких к
близких к![]() (т.е.
(т.е.![]() ограничена в окрестности точки
ограничена в окрестности точки![]() ),
то
),
то![]() .
.
Пример
8.  ,
т.к.
,
т.к.![]() ,
а
,
а
Пример
9.  т.к.
т.к.![]() и
и![]() при
при![]() .
.
