
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Непрерывность функции в
Рассмотрим
функцию
![]() ,
определенную в области
,
определенную в области![]() .
Предположим, что лишь одна переменная
.
Предположим, что лишь одна переменная![]() получила приращение
получила приращение![]() ,
а остальные переменные остались
неизменными. Тогда разность:
,
а остальные переменные остались
неизменными. Тогда разность:
![]()
называется
частным приращением функции
![]() по переменной
по переменной![]() .
.
Функция
![]() называетсянепрерывной по переменной
называетсянепрерывной по переменной![]() ,
если функция определена как в точке
,
если функция определена как в точке![]() ,
так и в точке
,
так и в точке![]() ,
и эти точки являются точками сгущения
этой функции. При этом должно выполняться
условие
,
и эти точки являются точками сгущения
этой функции. При этом должно выполняться
условие![]() ,
т.е. бесконечно малым приращениям
переменной
,
т.е. бесконечно малым приращениям
переменной![]() должны соответствовать бесконечно
малые частные приращения функции
должны соответствовать бесконечно
малые частные приращения функции![]() .
.
Если приращение получают все переменные, то соответствующее приращение функции:
![]() называется
полным приращением функции (или просто
приращением функции).
называется
полным приращением функции (или просто
приращением функции).
Естественно, что во всех точках, соответствующих как частным приращениям, так и полному приращению функции, сама функция должна быть определена.
Также следует отметить, что полное приращение функции, вообще говоря, не равно сумме частных приращений:
 .
.
Функция
многих переменных, определенная в
![]() ,
называется непрерывной в точке сгущения
,
называется непрерывной в точке сгущения![]() ,
если:
,
если:
 ;
; ;
; .
.
Из данного определения следует, что:
функция должна быть определена в точке
 и эта точка должна быть предельной в
области существования функции;
и эта точка должна быть предельной в
области существования функции;приращение
 для любой непрерывной функции является
величиной бесконечно малой:
для любой непрерывной функции является
величиной бесконечно малой: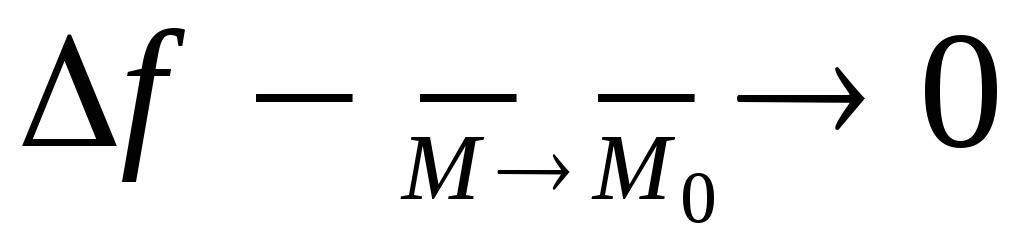 причем это условие должно выполняться
и для всех частных приращений функции
причем это условие должно выполняться
и для всех частных приращений функции .
.
Таким
образом, для выполнения требования
непрерывности функции нескольких
переменных в точке необходимо, чтобы
функция была непрерывна как в самой
точке, так и в некоторой окрестности
этой точки, причем при достаточно малых
по абсолютной величине приращениях
переменных
![]() .
.
Непрерывность на множестве
Функция
![]() называется непрерывной на множестве
называется непрерывной на множестве![]() ,
если она непрерывна во всех точках этого
множества.
,
если она непрерывна во всех точках этого
множества.
Непрерывные функции многих переменных обладают следующими свойствами:
Композиции
![]() функций
функций![]() и
и![]() вида:
вида:
 ;
; ;
; ;
;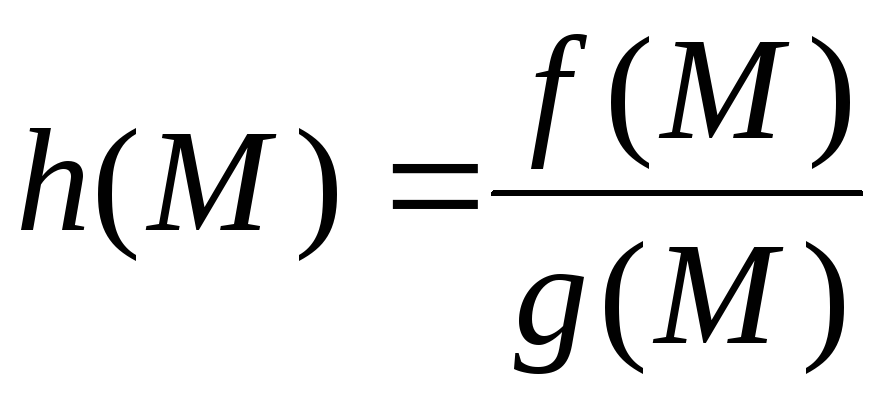 при
при
 являются непрерывными в точке
являются непрерывными в точке ,
если
,
если и
и непрерывными в точке
непрерывными в точке .
.
По аналогии с понятием сложной функции одной переменной для функций нескольких переменных можно ввести понятие суперпозиции функций.
Если
функция
![]() определена в области
определена в области![]() ,
а семейство функций
,
а семейство функций![]() определено
в
определено
в![]() и области изменения функций этого
семейства
и области изменения функций этого
семейства![]() содержатся во множестве
содержатся во множестве![]() ,
то в
,
то в![]() задана сложная зависимость
задана сложная зависимость![]() .
Если функция
.
Если функция![]() определена в области
определена в области![]() и непрерывна в
и непрерывна в![]() ,
а функции
,
а функции![]() определены в
определены в![]() и непрерывны в
и непрерывны в![]() ,
то при условии, что
,
то при условии, что![]() ,
функция
,
функция![]() является непрерывной в точке
является непрерывной в точке![]() ,
то есть
,
то есть![]() .
.
Теоремы о непрерывности
Теоремы Больцано-Коши и Вейерштрасса о непрерывности могут быть сформулированы и для функций многих переменных, однако в этом случае они имеют свою специфику, обусловленную более сложной природой множеств, на которых заданы функции, а также природой самих функциональных объектов.
Предварительно
желательно ввести следующие геометрические
истолкования функциональных объектов
в
![]() :
:
 определенная на
области
определенная на
области
 может рассматриваться как гиперповерхность
в
может рассматриваться как гиперповерхность
в мерном
пространстве переменных
мерном
пространстве переменных ;
; гиперкривая,
которая задается как суперпозиция
функции
гиперкривая,
которая задается как суперпозиция
функции
 и параметрических зависимостей
и параметрических зависимостей .
.
Если
области изменения функций семейства
![]() содержатся во множестве
содержатся во множестве![]() ,
то график гиперкривой целиком располагается
на гиперповерхности
,
то график гиперкривой целиком располагается
на гиперповерхности![]() .
.
Первая
теорема Больцано-Коши.Пусть
функция
![]() определена
и непрерывна в замкнутой и связной
области
определена
и непрерывна в замкнутой и связной
области![]() .
Если в двух точках области
.
Если в двух точках области![]() и
и![]() выполняется условие
выполняется условие![]() ,
то на гиперкривой, соединяющей
,
то на гиперкривой, соединяющей![]() и
и![]() существует точка
существует точка![]() такая, что
такая, что![]() .
.
Вторая
теорема Больцано-Коши.Пусть
функция
![]() определена и непрерывна в
замкнутой и связной области
определена и непрерывна в
замкнутой и связной области
![]() .
Если в двух точках области
.
Если в двух точках области![]() и
и![]() выполняется условие
выполняется условие![]()
![]() ,
то
,
то![]() ,
удовлетворяющего условию
,
удовлетворяющего условию![]() ,
существует точка
,
существует точка
![]() такая, что
такая, что![]() .
Т.е. на каждом отрезке функция принимает
все свои промежуточные значения.
.
Т.е. на каждом отрезке функция принимает
все свои промежуточные значения.
Теоремы
Больцано-Коши требуют соблюдения условий
связности области
![]() .
При этом сама область может быть
неограниченной, в то время как теоремы
Вейерштрасса требуют, чтобы область
была ограниченной, но не требуют
обязательности выполнения условия
связности.
.
При этом сама область может быть
неограниченной, в то время как теоремы
Вейерштрасса требуют, чтобы область
была ограниченной, но не требуют
обязательности выполнения условия
связности.
Первая
теорема Вейерштрасса.Если
функция
![]() определена и непрерывна в ограниченной
и замкнутой области
определена и непрерывна в ограниченной
и замкнутой области![]() ,
то она ограничена в этой области.
,
то она ограничена в этой области.
Вторая
теорема Вейерштрасса.Если
функция
![]() определена и непрерывна в ограниченной
и замкнутой области
определена и непрерывна в ограниченной
и замкнутой области![]() ,
то она имеет минимум и максимум в этой
области.
,
то она имеет минимум и максимум в этой
области.
Таким образом, математический инструментарий, отработанный на элементарном и наглядном объекте – функциях одной переменной, легко переносится на объекты более сложной природы – функции многих переменных.
