Линейные неоднородные уравнения второго порядка с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение второго порядка с постоянными коэффициентами , гдеи– данные постоянные числа и– известная функция от.

Теорема. Общее решение неоднородного уравнения второго порядка с постоянными коэффициентами равно сумме общего решения однородного уравненияи частного решения данного неоднородного уравнения.

Доказательство. Пустьесть общее решение уравнения , а– некоторое частное решение уравнения . Если подставить решения в соответствующие исходные уравнения получим:и. Складывая почленно, приходим к равенству:. Отсюда ясно, что функциябудет общим решением уравнения, поскольку оно содержит две независимые произвольные постоянныеи.

Поскольку решение однородного уравнения второго порядка с постоянными коэффициентами рассматривалось ранее, то необходимо только указать способ нахождения частного решения .

1. Правая часть уравнения является показательной функцией . Тогда частное решение также ищется в виде показательной функции, где– неопределенный коэффициент. Отсюда,и. Подставив в исходное уравнение и сократив на, получим.

Возможны два случая:

• не является корнем характеристического уравнения, т.е. , тогдаи, следовательно,;

• Если – простой корень, то решение следует искать в виде; если– кратный корень, то решение следует искать в виде.

2. Правая часть уравнения является тригонометрическим полиномом . Тогда частное решение этого уравнения ищется также в форме тригонометрического полинома, гдеи– неопределенные коэффициенты. Дифференцируяполучим:

; .

Подставив в исходное уравнение и сгруппировав коэффициенты при тригонометрических функциях, получим:

Так как последнее равенство представляет собой тождество, то коэффициенты при тригонометрических функциях должны быть равны между собой:

Из этой системы и определяются коэффициенты и. Эта система несовместна только в том случае, когда,(т.е. когда– корни характеристического уравнения). Тогда частное решение следует искать в виде.

3. Правая часть уравнения является полиномом, например, второй степени .

Тогда частное решение также следует искать в форме полинома второй степени . В результате дифференцирования получим,. Подставляя,ив исходное уравнение приходим к тождеству:

или

.

Так как два многочлена тождественно равны друг другу тогда и только тогда, когда коэффициенты при одинаковых степенях переменной равны, то для определения коэффициентов,иполучается система:

Если , то из этой системы для коэффициентов,иполучаются вполне определенные значения. Частное значение в этом случае также будет вполне определено.

Если (характеристическое уравнение имеет простой нулевой корень), то система уравнений несовместна. В этом случае, полагая, что, частное решение следует искать в виде. Эта задача решается аналогично, еслиявляется полиномом какой-нибудь другой степени.

Линейные дифференциальные уравнения-го порядка

Линейным дифференциальным уравнением -го порядка называется уравнение вида:

Если , то уравнение называется однородным. В противном случае, если тождествоне выполняется, уравнение называется неоднородным.

Для более компактной записи введем обозначение:

Свойства решений линейного дифференциального уравнения n-го порядка:

1. Для любых функций 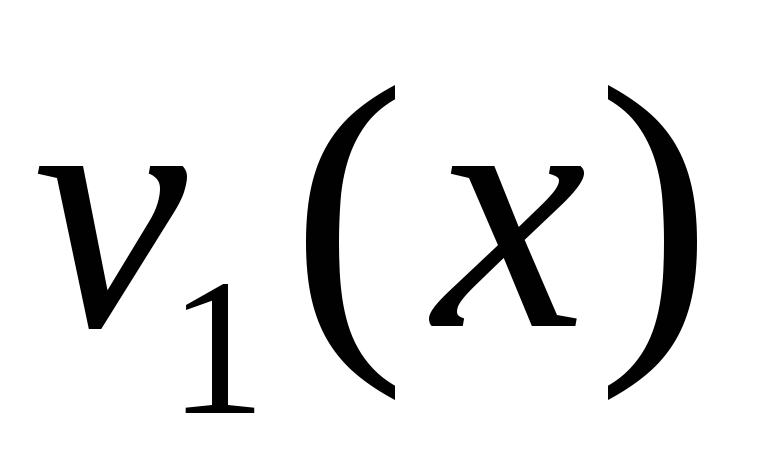и

;

2. Для любого числа и функции;

3. Если ,, …,– решения однородного дифференциального уравнения, а– частное решение неоднородного дифференциального уравнения, то для любых чисел,, …,функцияявляется решением неоднородного уравнения.

Для построения общего решения линейного дифференциального уравнения необходимо обобщить понятие линейной независимости на систему функций.

Определение. Система функций ,, …,называется линейно независимой на множестве, если тождественное равенствоимеет единственно возможное решение.

Предположим, что функции ,, …,непрерывны и имеют непрерывные производные дого порядка включительно на множестве .

Тогда определитель:

называется определителем Вронского.

Известно, что определитель Вронского, составленный из решений линейного однородного дифференциального уравнения, обладает следующим свойством.

Теорема. Определитель Вронского для решений линейного однородного дифференциального уравнения тождественно равен нулю, когда решения линейно зависимы и не равен нулю ни в одной точке, когда решения линейно независимы на множестве.

Теорема. Общее решение линейного однородного дифференциального уравнения имеет вид:

,

где ,, …,– решения однородного дифференциального уравнения,– частное решение неоднородного дифференциального уравнения.

Линейно независимая система решений ,, …,линейного однородного дифференциального уравнения называетсяфундаментальной системой решений.