Необходимые условия дифференцируемости. Достаточные условия

Наличие конечной производной является необходимым и достаточным условием для дифференцируемости функции одной переменной. Для функции нескольких переменных существование конечных частных производных по всем независимым переменным, т.е. существование вектора-градиента в точке–необходимоеусловие дифференцируемости функции. Однако это условие не является достаточным для дифференцируемости функции многих переменных.

Достаточноеусловие дифференцируемости.

Теорема. Для того чтобы , определенная в областии непрерывная в точкебыла дифференцируема в этой точке, достаточно, чтобы эта функция имела непрерывные частные производныев некоторой окрестности, и эти частные производные были непрерывны в точке.

Следствием теоремы является существование в некоторой окрестности точки ограниченного вектора-градиента, непрерывного в.

Дифференцирование функции, заданной неявно и композиции функций

Функция переменныхназывается заданной неявно, если она задана уравнением, не разрешенным относительно. В этом случае частные производные функциинаходятся в результате дифференцирования функциипо свободным переменными по зависимой переменной.

В случае, если – функция одной переменной, заданная уравнением, то.

В двумерном случае, если – функция двух переменныхи, заданная уравнением, то.

В общем случае, если – функцияпеременных, заданная уравнением, то частные производные находятся по формулам:

, , … ,.

Если в задана сложная зависимость, т.е. функцияопределена в области, а семейство функцийопределены ви области изменения функций этого семействасодержатся во множестве, то если функцияопределена в областии непрерывна в, а семейство функцийопределены в, непрерывны ви имеет в этой точке непрерывные первые производные, а также при условии, что функции:

являются непрерывными в точке и имеют в этой точке непрерывные первые производные, то.

Тогда при дифференциальном анализе функциональной зависимости справедливы следующие соотношения:

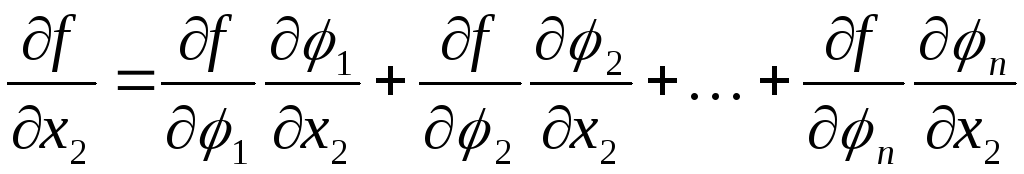
Если сложная функция имеет в точке непрерывные первые производные, то она является дифференцируемой в этой точке, и ее полный дифференциал первого порядка обладает свойством инвариантности и имеет вид:

Различие между полными дифференциалами простой и сложной функций состоит в том, что для простой функции приращение независимой переменной равно ее дифференциалу, а для сложных функций это равенство не выполняется.

Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала

Частными производными функции в том случае, если они существуют не в одной точке, а на некотором множестве, являются функции, определенные на этом множестве. Эти функции могут быть непрерывными и в некоторых случаях также могут иметь частные производные в различных точках области определения.

Частные производные от этих функций называютсячастными производными второго порядка или вторыми частными производными.

Частные производные второго порядка разбиваются на две группы:

• вторые частные производные от по переменной;

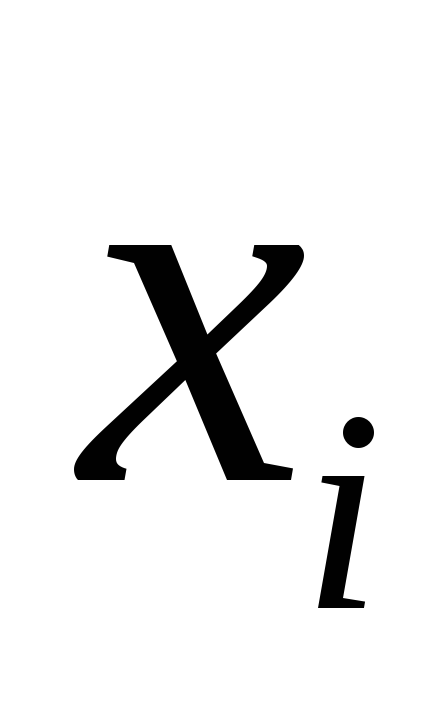• смешанные частные производные от по переменными.

При последующем дифференцировании можно определить частные производные третьего порядка и т.д. Аналогичными рассуждениями определяются и записываются частные производные высших порядков.

Теорема.Если все входящие в вычисления частные производные, рассматриваемые как функции своих независимых переменных, непрерывны, то результат частного дифференцирования не зависит от последовательности дифференцирования.

Часто возникает потребность решения обратной задачи, которая состоит в определении того, является ли полным дифференциалом функциивыражение вида, гденепрерывные функции с непрерывными производными первого порядка.

Необходимое условие полного дифференциала можно сформулировать в виде теоремы, которую примем без доказательства.

Теорема.Для того, чтобы дифференциальное выражение являлось в областиполным дифференциалом функции, определенной и дифференцируемой в этой области, необходимо, чтобы в этой области тождественно было выполнено условиедля любой пары независимых переменныхи.

Задача вычисления полного дифференциала второго порядка функции может быть решена следующим образом. Если выражение полного дифференциалатакже является дифференцируемым, то вторым полным дифференциалом (или полным дифференциалом второго порядка) можно считать выражение, полученное в результате применения операции дифференцирования к первому полному дифференциалу, т.е.. Аналитическое выражение для второго полного дифференциала имеет вид:

.

С учетом того, что смешанные производные не зависят от порядка дифференцирования, формулу можно сгруппировать и представить виде квадратичной формы:

.

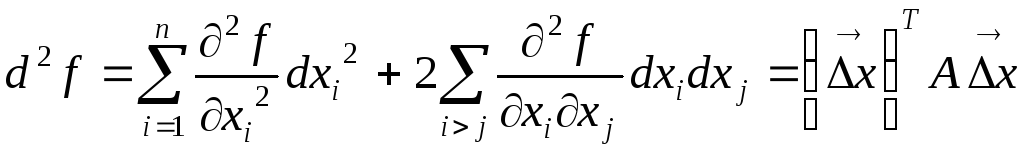Матрица квадратичной формы равна:

Пусть задана суперпозиция функций , определенной ви

, определенных в . При этом. Тогда, еслииимеют непрерывные частные производные до второго порядка в точкахи, то существует второй полный дифференциалсложной функции следующего вида:

, т.е.

Как видно, второй полный дифференциал не обладает свойством инвариантности формы. В выражение второго дифференциала сложной функции входят слагаемые вида , которые отсутствуют в формуле второго дифференциала простой функции.

Построение частных производных функции более высоких порядков можно продолжать, выполняя последовательное дифференцирование этой функции:

, где индексы принимают значения отдо, т.е. производная порядкарассматривается, как частная производная первого порядка от производной порядка. Аналогично можно ввести и понятие полного дифференциала порядкафункции _, как полного дифференциала первого порядка от дифференциала порядка:.

В случае простой функции двух переменных формула для вычисления полного дифференциала порядка функцииимеет вид .

Применение оператора дифференцирования позволяет получить компактную и легко запоминающуюся форму записи для вычисления полного дифференциала порядка функции, аналогичную формуле бинома Ньютона. В двумерном случае она имеет вид: .