
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Непрерывность функции
Рассмотрим
функцию
![]() ,
определенную на промежутке
,
определенную на промежутке![]() Пусть
Пусть![]() .
Функция
.
Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если
,
если
![]()
Функция
![]() называетсянепрерывной слева (справа)в точке
называетсянепрерывной слева (справа)в точке![]() ,
если
,
если![]()
![]() .
Естественно, при этом функция
.
Естественно, при этом функция![]() должна быть определена в некоторой
окрестности слева (справа) то точки
должна быть определена в некоторой
окрестности слева (справа) то точки![]() .
Непрерывность функции в точке
.
Непрерывность функции в точке![]() означает непрерывность этой функции в
указанной точке как слева, так и справа.
означает непрерывность этой функции в
указанной точке как слева, так и справа.
Функция
![]() ,
определенная на интервале
,
определенная на интервале![]() называетсянепрерывной на интервале
называетсянепрерывной на интервале
![]() ,
если она непрерывна в каждой точке
,
если она непрерывна в каждой точке![]() этого интервала
этого интервала![]() .
.
Функция
![]() ,
определенная на отрезке
,
определенная на отрезке![]() (
(![]() )
называетсянепрерывной на отрезке
)
называетсянепрерывной на отрезке ![]() ,
если она непрерывна в каждой точке
,
если она непрерывна в каждой точке![]() интервала
интервала
![]() ,
непрерывна справа в точке
,
непрерывна справа в точке![]() и непрерывна слева в точке
и непрерывна слева в точке![]() .
.
Общие
свойства непрерывных функций, заданных
на отрезке
![]() ,
определяются четырьмя теоремами: двумя
теоремами Больцано–Коши и двумя
теоремами Вейерштрасса.
,
определяются четырьмя теоремами: двумя
теоремами Больцано–Коши и двумя
теоремами Вейерштрасса.
Теорема
(первая теорема Больцано–Коши).Пусть функция
![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке![]() ,
и на концах этого промежутка принимает
значения разных знаков; тогда найдется
точка
,
и на концах этого промежутка принимает
значения разных знаков; тогда найдется
точка![]() ,
в которой функция равна нулю.
,
в которой функция равна нулю.
Теорема
(вторая теорема Больцано–Коши).Пусть функция
![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке![]() .
Тогда, если
.
Тогда, если![]() то функция принимает все свои промежуточные
значения, принадлежащие промежутку
то функция принимает все свои промежуточные
значения, принадлежащие промежутку![]() ,
где
,
где![]() ,
,![]() ,
т.е.
,
т.е.![]() .
.
Теорема
(первая теорема Вейерштрасса).Пусть
функция
![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке![]() ,
тогда функция
,
тогда функция![]() является ограниченной на этом отрезке.
является ограниченной на этом отрезке.
Теорема
(вторая теорема Вейерштрасса).Пусть
функция
![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке![]() ,
тогда функция
,
тогда функция![]() имеет минимум и максимум на этом отрезке
(множество значений функции включает
в себя точные верхнюю и нижнюю границы).
имеет минимум и максимум на этом отрезке
(множество значений функции включает
в себя точные верхнюю и нижнюю границы).
Отметим, прежде всего, что основные элементарные функции непрерывны во всех точках, в которых они определены. К основным элементарным функциям относятся:
Постоянная функция
 .
Область определения
.
Область определения ;
;Идентичная функция
 .
Область определения
.
Область определения ;
;Одночлен
 ,
, ;
;Многочлен
 ,
, ;
;Рациональная функция
 ,
где
,
где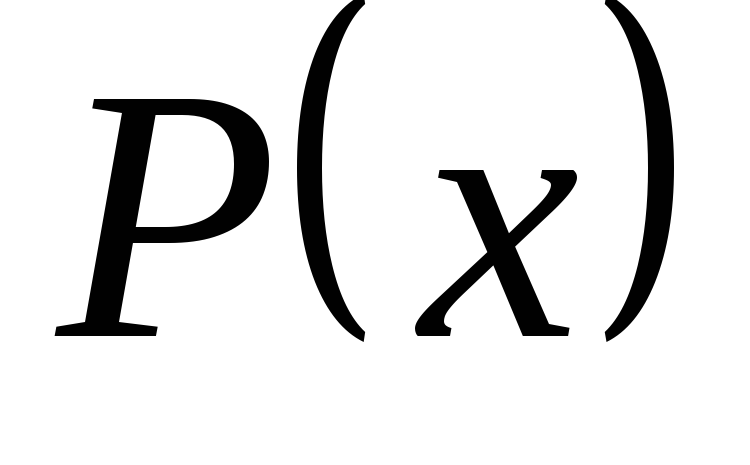 и
и ‑ многочлены. Функция определена
при всех
‑ многочлены. Функция определена
при всех ,
кроме корней многочлена
,
кроме корней многочлена ;
;Степенная функция
 .
Если
.
Если ,
то функция определена, по крайней мере,
на
,
то функция определена, по крайней мере,
на .
При
.
При определена, по крайней мере, на
определена, по крайней мере, на .
(При некоторых
.
(При некоторых степенная функция может быть определена
на более широком множестве. Например,
функция
степенная функция может быть определена
на более широком множестве. Например,
функция имеет область определения
имеет область определения .
Функция
.
Функция определена на
определена на );
);Показательная функция
 ,
, ,
, .
Определена на
.
Определена на ;
;Логарифмическая функция
 ,
, ,
, .
Определена на
.
Определена на ;
;Синус
 ,
косинус
,
косинус определены на
определены на .
Эти функции являются периодическими
с периодом
.
Эти функции являются периодическими
с периодом ,
т.е.
,
т.е. ,
для любого
,
для любого из
из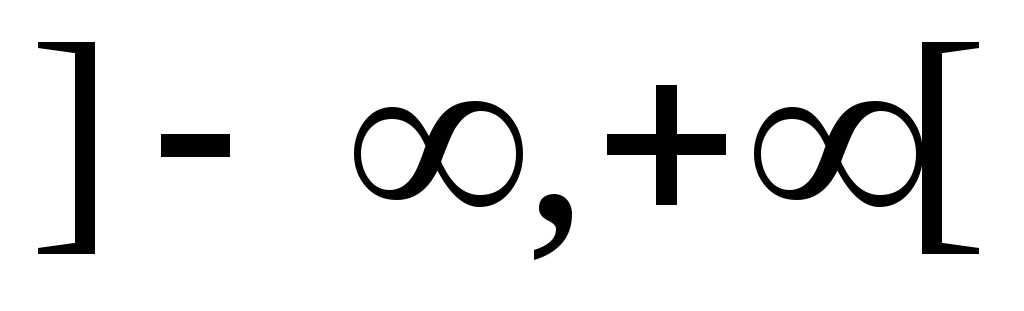 ;
;Арксинус
 и арккосинус
и арккосинус определены на
определены на .
.
Если
![]() и
и![]() ‑ непрерывные функции, то их сумма,
разность и произведение являются
непрерывными функциями. Частное
непрерывных функций
‑ непрерывные функции, то их сумма,
разность и произведение являются
непрерывными функциями. Частное
непрерывных функций будет непрерывно всюду, где оно определено.
Таким образом, можно утверждать, что
всякая арифметическая комбинация
непрерывных функций непрерывна всюду,
где она определена.
будет непрерывно всюду, где оно определено.
Таким образом, можно утверждать, что
всякая арифметическая комбинация
непрерывных функций непрерывна всюду,
где она определена.
Непрерывность композиции
Пусть
задана функция
![]() ,
,![]() со значениями в
со значениями в![]() ,
и на множестве
,
и на множестве![]() определена функция
определена функция![]() со значениями в
со значениями в![]() .
Тогда для любого
.
Тогда для любого![]() можно вычислить
можно вычислить![]() ,
на
,
на![]() можно определить функцию
можно определить функцию![]() со значениями в
со значениями в![]() по правилу:
по правилу:![]()
![]() .
Говорят, что функция
.
Говорят, что функция![]() есть композиция функций
есть композиция функций![]() и
и![]() и обозначают
и обозначают![]() .
(Функцию
.
(Функцию![]() называют также сложной функцией).
называют также сложной функцией).
Если
функция
![]() непрерывна в точке
непрерывна в точке![]() ,
а функция
,
а функция![]() непрерывна в точке
непрерывна в точке![]() ,
то композиция
,
то композиция![]() непрерывна в точке
непрерывна в точке![]() .
Говоря короче (хотя и менее строго),
композиция непрерывных функций
непрерывна.
.
Говоря короче (хотя и менее строго),
композиция непрерывных функций
непрерывна.
Пример
14. Функция![]() непрерывна на
непрерывна на![]() ,как композиция непрерывных функций
,как композиция непрерывных функций![]() и
и![]() ,
поскольку такая композиция определена
для
,
поскольку такая композиция определена
для![]() .
.
