10.2. Динамика специальной теории относительности
10.2.1. Релятивистский импульс
Классическое выражение для импульса частицы массой m
.
не
инвариантно относительно преобразований
Лоренца. Учитывая, что при малых скоростях
собственное время частицы d(время по часам, движущегося вместе с
частицей) близко ко времениdt,
измеренному по часам в неподвижной
системе отчета, т. е.
.
Запишем выражение для импульса (10.37) следующим образом:
,
где dr – вектор перемещения частицы.
Проверим инвариантность определения (10.37) по отношению к преобразованиям Лоренца. Рассмотрим процесс абсолютно упругого столкновения частиц с массами m1 и m2 в системах К и К, предполагая, что закон сохранения импульса справедлив в системе отсчета К. Запишем уравнение закона сохранения импульса:
,
здесь правая часть равенства представляет собой полный импульс системы частиц до столкновения, левая – после столкновения.
Проецируя соотношение (10.38) на оси x, y, z. Получаем:
Перейдем к системе К, имея в виду что собственное время d – инвариантно:
Проекции перемещений dr10 и dr20 в направлении оси x испытают лоренцево сокращение, в направлении осей y и z не изменятся:
.
Разделим
первое равенство системы (10.39) на
.
Учитывая соотношения (10.40) и (10.41), получим:
Возвращаясь к векторной записи, имеем:
.
Таким образом, выражение для импульса (10.37) оказывается инвариантным относительно преобразований Лоренца, и, соответственно, закон сохранения импульса в СТО выполняется.
Так как собственное время частицы связано с временем t в системе К, относительно которой наблюдается движение тела, то для импульса в системе К получим:
.
Очевидно, что при V<<c соотношение (10.43) переходит в выражение для классического импульса P=mV. Иногда формулу (10.43) трактуют иначе: импульс, как в классической механике Ньютона, определяются выражением P=mV, но массу тела считают не инвариантной величиной, а зависящей от скорости:
.
Масса mr, определяемая соотношением (10.44) называется релятивистской массой; инвариантной массой является m0 – масса покоя. Таким образом, релятивистский импульс принято записывать так:
.
10.2.2. Основное уравнение динамики сто
Основное уравнение динамики тела с массой m – уравнение второго закона Ньютона:
.
Если для импульса частицы использовать релятивистское выражение (10.45), то подстановка его в (1.46) дает выражение, инвариантное относительно преобразований Лоренца:
.
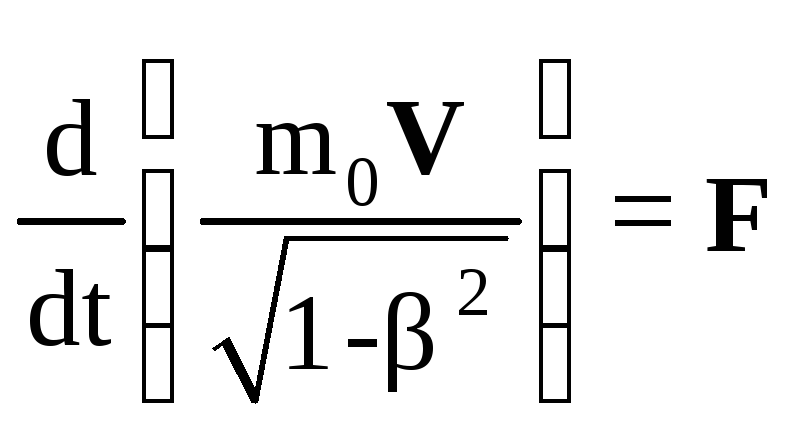Уравнение (10.47) называют основным уравнением динамики СТО.
10.2.3. Релятивистское выражение для энергии
Умножим обе части (10.47) на перемещение частицы dr=Vdt:
.
Правая часть (10.48) равна элементарной работе dA силы F на перемещении dr. По закону сохранения энергии эта работа идет на увеличение полной энергии частицы:
Fds = dE.
следовательно:
.
Таким образом, приходим к соотношению:
.
Интегрируя обе части (10.48), получим:
.
Соотношение (10.49) оказывается инвариантным по отношению к преобразованиям Лоренца, если постоянная интегрирования равна нулю.
Итак:
.
При V=0 соотношение (10.50) принимает вид:
,
где использовано обозначение E0 для неподвижного тела. Эту энергию называют энергией покоя или собственной энергией тела. Энергия покоя – это внутренняя энергия, не связанная с перемещением тела в пространстве как целого и/или его положением во внешнем потенциальном поле. В нее входит потенциальная энергия взаимодействия частиц тела между собой и кинетическая энергия движения этих частиц около общего центра масс.
Кинетическую энергию тела определяют как разность полной релятивистской энергии (10.50) и энергии покоя (10.51):
.
При малых скоростях (0), можно, используяприближенную формулу
,
где х=2 привести соотношение (10.53) к обычному видуклассической механики Ньютона:
Сравнивая (10.50) с выражением для импульса (10.43), получим:
.