1.8.1. Сложение колебаний одного направления

Пусть материальная точка одновременно участвует в двух колебаниях ₁ и ₂ одного направления и одной частоты :

По принципу суперпозиции результирующее смещение равно алгебраической сумме смещений, полученных в каждом из колебаний, т. е.:

.

Предположим, что амплитуды обоих колебаний равны, т. е. а₁=а₂=а. Используем тригонометрическую формулу для суммы двух косинусов и преобразуем формулу (1.39):

Таким образом, при суперпозиции колебаний одной частоты, одного направления и одинаковой амплитуды возникает гармоническое колебание с той же самой частотой , и амплитудой, зависящей от разности начальных фаз колебаний и равной

.

В частности: при ₁₀=₂₀ имеем А_РЕЗ=2а, при ₁₀=₂₀ амплитуда результирующего колебания равна нулю.

1. 1.8.2. Биения

Рассмотрим суперпозицию двух гармонических колебаний одинаковой амплитуды и одного направления, частоты которых ₁ и ₂ отличаются незначительно (₁₂=)

, .

Результирующее колебание равно:

.

Используя известные тригонометрические формулы, приведем (1.41) к следующему виду

.

Очевидно, что первый сомножитель гармонически изменяется с частотой =(₁+₂)/2₁₂. Второй множитель осциллирует с малой частотой (₁-₂)/2, а значит, имеет большой период. Таким образом, колебание (1.43) можно рассматривать как гармоническое колебание с частотой :

,

амплитуда которого А равна:

.

Амплитуда медленно изменяется во времени – пульсирует.

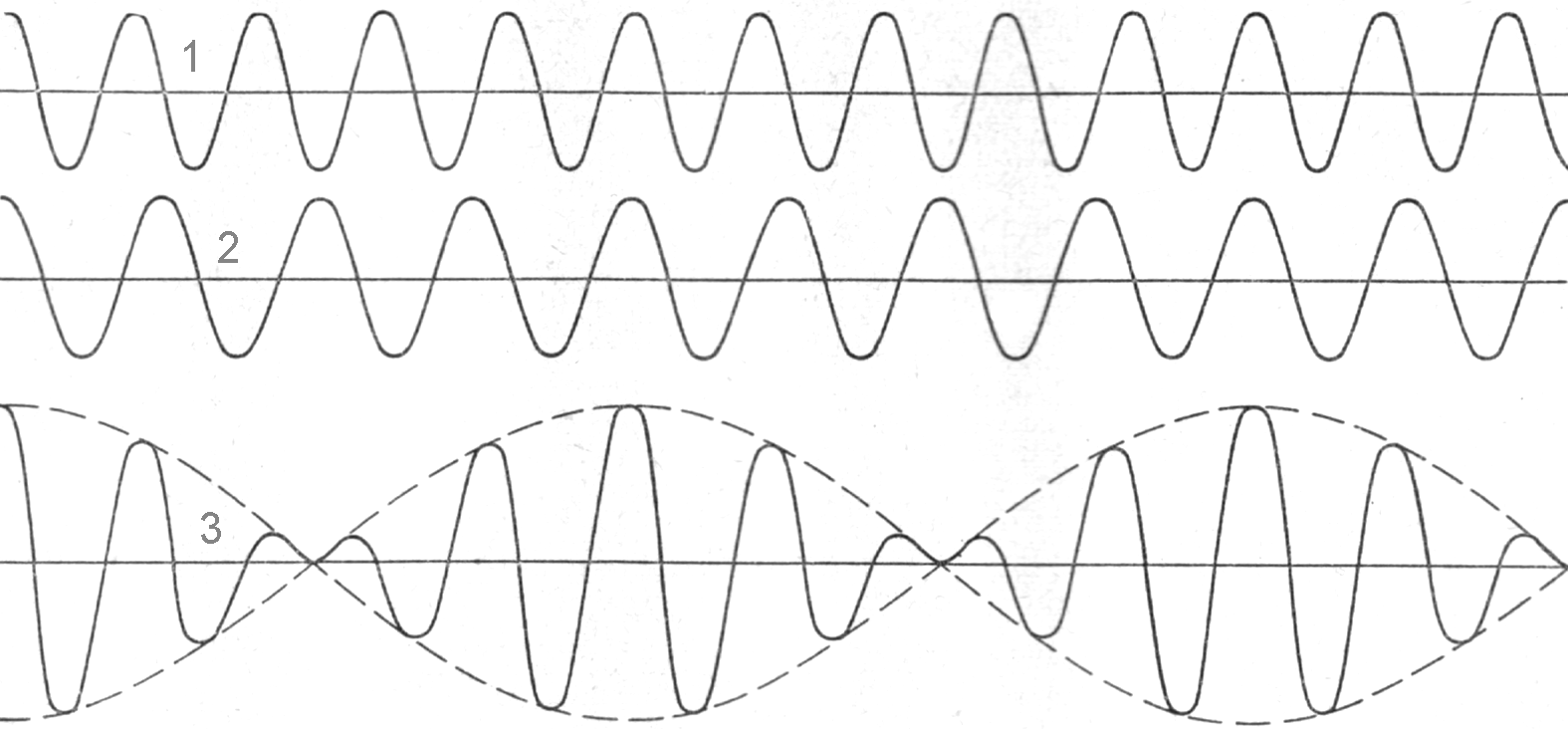
Характер изменения во времени величины , порожденной наложением колебаний с отношением частот 8:10 показан на рисунке 1.7.

Изображенное на рисунке постепенное нарастание и уменьшение амплитуды результирующих колебаний и носит название “биения”.

Используя условие периодичности функции (t)=(t+T) можно показать, что при рациональном отношении частот колебаний ₁:₂=n₁:n₂, (n₁:n₂ – целые числа) функция  является периодической с периодом Т равным

.

Рис. 1.7.

(1) - колебания ₁ = а cos 10t, (2) колебание ₂ = а cos 8t, (3) результирующее колебание

Если частоты исходных колебаний не соизмеримы, т. е. их отношение ₁:₂ не равно отношению некоторых целых чисел n₁ и n₂, то результирующее колебание не является периодическим.

1.8.3. Сложение взаимно перпендикулярных колебаний

Сложение колебаний c рациональным отношением частот, но направленных вдоль взаимно перпендикулярных осей X и Y

экспериментально исследовал А. Лиссажу. Он показал, что точка, участвующая в таких колебаниях, движется по плоским замкнутым траекториям, которые получили, в последствии, название фигур Лиссажу.

Пусть материальная точка участвует в двух колебаниях, определяемых уравнениями (1.46). Найдем уравнение траектории Ф(X,Y)=0 материальной точки на координатной плоскости X,Y. Для упрощения предположим, что частоты колебаний равны, а начальная фаза первого колебания равна нулю (этого можно добиться соответствующим выбором начального момента времени), начальную фазу второго колебания обозначим через . Уравнения колебаний примут вид:

.

Для нахождения траектории (исключения параметра t) поступим следующим образом: из первого уравнения системы (1.47) выразим cost,

,

тогда:

.

Представляя cos(t+) как косинус суммы двух углов из второго уравнения (1.47) имеем

.

Используя выражения для тригонометрических функций аргумента t, соотношение (1.48) можно записать следующим образом:

.

Возводя в квадрат и произведя перегруппировку, получим:

.

Из аналитической геометрии известно, что уравнение (1.49) является уравнением эллипса, оси которого повернуты относительно осей координат X и Y. Ориентация осей эллипса и размеры его полуосей достаточно сложно зависят от разности фаз колебаний =₂-₁=₂.

Частные случаи.

1. Разность фаз исходных колебаний равна нулю (=0). Уравнение (1.49) принимает вид:

,

т. е. представляет собой полный квадрат, поэтому:

.

Решением полученного уравнения является функция

.

2. Разность фаз колебаний равна . Уравнение (1.49) приводится к виду

.

Аналогично предыдущему случаю получаем:

.

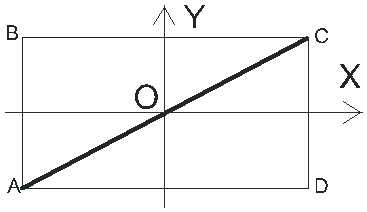
Уравнения (1.50) и (1.51) являются уравнениями прямых, тангенсы наклона которых равны b/a и -b/a, соответственно. Частица движется по соответствующей диагонали прямоугольника ABCD со сторонами a и b (см. рис. 1.8).

а

b

Рис. 1.8. a - движение описывается уравнением (1.50), и b - уравнением (1.51)

3. Разность фаз колебаний равна /2. Уравнение результирующего движения (1.49) принимает вид

,

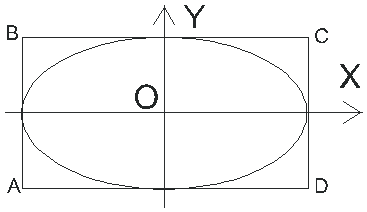
т. е. представляет собой эллипс, приведенный к координатным осям X и Y, полуоси эллипса равны амплитудам a и b складывающихся колебаний.

Рис. 1.9. Результат наложения взаимноперпендикулярных колебаний с разностью фаз равной /2

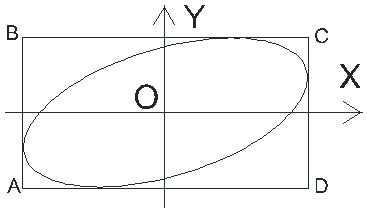
4. При произвольной разности фаз  колебаний траектория представляет собой эллипс, вписанный в прямоугольник со сторонами 2a и 2b. Траектории, рассмотренные в пунктах 1 и 2 можно рассматривать как эллипсы, вырожденные в отрезок. Если полуоси эллипса (амплитуды складываемых колебаний) равны между собой, то эллипс вырождается в окружность (a=b).

Рис. 1.10. Результат наложения взаимно перпендикулярных колебаний с произвольной разностью фаз

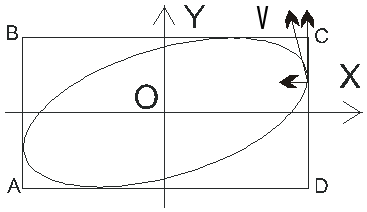
5. Разность фаз  определяет также направление движения материальной точки по траектории. Уравнения (1.47) в параметрической форме при величине  равной -/2 могут быть записаны так:

.

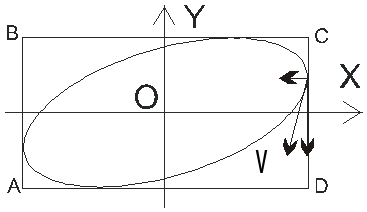
После начала движения, т. е. при t>0 величина Х начнет уменьшаться, Y – будучи величиной положительной, будет возрастать. Этим изменениям, как видно из рисунка 1.11а, соответствует движение материальной точки со скоростью V против направления движения часовой стрелки. Если разность фаз  равна /2, то уравнения (1.47) имеют вид

с началом движения координаты X и Y будут уменьшаться, что указывает на то, что точка движется по эллипсу в направлении движения часовой стрелки (см. рис. 1.11b).

6. Если частоты взаимно перпендикулярных колебаний не равны друг другу (_X_Y), то траектории движущихся точек представляются сложными кривыми. Во всех случаях, когда отношение _X/_Y является рациональным числом, траектория точки является замкнутой линией. Вид траектории зависит также от разности фаз исходных колебаний.

a

b

Рис 1.11. К вопросу о направлении движения частицы. V указывает направление скоростей частиц, стрелки – составляющие скоростей вдоль осей координат

Если отношение частот колебаний вдоль осей Х и Y (_X:_Y) не является рациональным числом, то траектория точки, участвующей в этих колебаниях – незамкнутая линия. С течением времени линия заполняет равномерно всю прямоугольную часть координатной плоскости размером 2a  2b.