1.9. Кинематика волнового движения

• Волной, или волновым движением, называют процесс распространения колебаний.

Волны, в отличие от колебаний, локализованных в некоторой конечной области пространства, могут распространяться не только в закрытых системах, но и в открытых. Открытыми системами называют системы, не имеющие пространственных границ, или, наоборот, системы, ограниченные какими-либо стенками с поглощающими покрытиями. Благодаря этим условиям в открытых системах отсутствует отражение и возвратное движение волн, а значит, отсутствуют такие явления, как эхо и резонанс.

Волны, как и колебания, необыкновенно широко распространены в окружающем мире; они очень разнообразны по физической природе. Выделяют упругие механические волны, звуковые волны, называемые просто звуком, световые волны и радиоволны, плазменные, волны вероятности и др. С формальной точки зрения все волны описываются одним и тем же уравнением.

Волны, образованные за счет внешнего периодического воздействия, называются бегущими волнами. Если внешняя сила, вызывающая колебания источника, является гармонической, то вызванная ею волна будет также гармонической.

1.9.1. Уравнение плоской волны

Рис. 1.12. К выводу уравнения бегущей плоской волны

Рассмотрим общий случай, когда распространение колебаний, заданное направляющим вектором n, не совпадает с какой-либо из пространственных осей координат. Пусть в момент времениt=0 в начале координат – точке О, возникают гармонические колебания величины, описываемые уравнением

.

Благодаря конечной скорости Vраспространения волны в пространстве, колебания в точке М будут запаздывать во времени по отношению к колебаниям в точке О на время=ℓ/V, равное времени распространения волны от источника до точки М. С учетом запаздывания волна, распространяющаяся вдоль направленияn, описывается уравнением

,

где ℓ – расстояние от начала координат до точки наблюдения. Это расстояние, как видно из рисунка 1.12, равно проекции радиус-вектора rточки наблюдения на направлениеn:

.

Уравнение (1.53) можно записать так:

.

Полученное уравнение является уравнением гармонической волны, распространяющейся (бегущей) в направлении, заданном вектором n. Очевидно, что функция, описывающая бегущую волну, содержащая периодическую функцию косинуса или синуса, является периодической функцией двух аргументов: времениtи координаты Х.

• Гармоническаяволна– это волна, соответствующая распространению гармонических колебаний.

• Амплитудаволны– наибольшее значение колеблющейся величины.

• Фазаволны– величинаили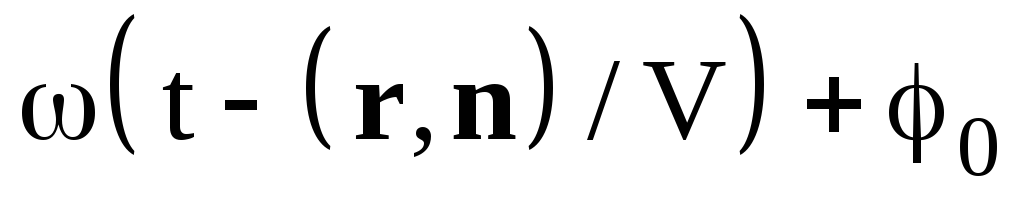=, равная аргументу функции косинуса (или синуса) в уравнении волны.

Отметим, что фаза колебания, приходящего от источника в некоторую точку пространства, увеличивается монотонно и линейно с течением времени, а при увеличении расстояния от источника до точки наблюдения фаза уменьшается.

• Начальнаяфазаволны₀– фаза в момент времениt=0; очевидно₀=(t=0).

Используя общепринятое обозначение для так называемого волнового вектора k (k=n/V), преобразуем уравнение волны (1.53) к виду:

Очевидно, что уравнение волны распространяющейся вдоль оси Х, имеет вид:

,

или

,

здесь kиiX– волновой вектор и радиус-вектор точки наблюдения с координатой Х.

Несложно показать, что уравнение волны распространяющейся в направлении, противоположном направлению оси Х, имеет вид:

. (1.56а)

• Волновойвектор– вектор, определяемый соотношением.

• Волновоечисло– это модуль волнового вектора: . Волновое число показывает, сколько длин волн укладывается на отрезке длиной 2метров.

Используя понятие волнового числа, уравнению волны бегущей вдоль оси х можно придать симметричный вид:

.

Наконец, учитывая разложение векторов kиrпо осям координат:и, запишем уравнение (1.54) следующим образом:

.

Из аналитической геометрии известно, что всякое уравнение первой степени с тремя переменными X,Y,Z вида

(*)

определяет в пространстве плоскость. Сравнение выражения (1.58) с (*) показывает, что коэффициент D играет роль фазы волны и содержит в себе зависимость от времени. Таким образом, уравнение (*) определяет положение некоторой плоскости в каждый момент времени. Во всех точках этой плоскости, называемой волновой поверхностью, фазы волны одна и та же.