Если сила имеет постоянную величину и направление (рис. 55), вектор f в формуле (24.9) можно вынести за знак интеграла, в результате чего выражение для работы примет вид

A = f ∫ds = fs = fsf ,

(24.12)

где s — вектор перемещения, а sf — его проекция на направление силы.

§25. Мощность

На практике имеет значение не только величина совершенной работы, но и время, в течение которого она совершается. Поэтому для характеристики механизмов, предназначенных для совершения работы, вводится величина, показывающая, какую работу данный механизм совершает в единицу времени. Эта величина называется мощностью. Таким образом, мощность W есть величина, равная отношению работы A к промежутку времени t, за который она совершается:

W =	A		(25.1)
	t
Если за одинаковые, сколь угодно малые промежутки времени			t совершается неодинаковая
работа A, мощность оказывается изменяющейся со временем. В этом случае вводится в
рассмотрение мгновенное значение мощности:
W = lim	A	= dA .	(25.2)
t→0	t	dt

В случае, когда мгновенная мощность (25.2) непостоянна, выражение (25.1) дает среднее значение мощности за промежуток времени t.

Пусть за время dt точка приложения силы получает перемещение ds. Тогда элементарная работа, dA совершаемая за время dt будет равна:

dA = fds,

и мощность можно представить в виде:

W = dAdt = f dsdt .

Но dsdt равно вектору скорости v . Следовательно, мощность оказывается равной скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения силы:

W = fv.

(25.3)

Единицы мощности. За единицу мощности принимается такая мощность, при которой в единицу времени (сек) совершается работа, равная единице (джилиэрг). В СИ единицей мощности является ватт (вт), равный джоулю в секунду (дж/сек). Единица мощности в СГС - системе (эрг/сек) специального названия не имеет. Соотношение между ваттом и эрг/сек: 1вт=107эрг/сек.

В МКГСС - системе единицей мощности служит лошадиная сила (л.с), равная 75 килограммометрам в секундах 1л.с.=736 вт

§26. Потенциальное поле сил. Силы консервативные и неконсервативные

Если тело поставлено в такие условия, что в каждой точке пространства оно подвержено воздействию других тел с силой закономерно изменяющейся от точки к точке говорят, что это тело находится в поле сил. Так, например, тело вблизи поверхности Земли находится в поле сил тяжести — в - каждой точке пространства на него действует сила P=mg направленная по вертикали вниз.

В качестве второго примера, рассмотрим тело M, «привязанное» пружиной к некоторому центру.O (Рис, 56). Один конец пружины может вращаться на шарнире вокруг неподвижной точки O в любом направлении, другой конец

62

Рис. 56.

прикреплен к телу M.В каждой точке пространства на тело M действует сила, направленная по радиусу (т. е, вдоль прямой, проходящей через центр O и тело M) и равная

f = −k(r − r0 ),

(26.1)

где r — расстояние тела от центра O, r0— длина недеформированной пружины, k — коэффициент пропорциональности. Если r>r0 (пружина растянута), сила направлена к центру и имеет знак «—» (направления силы и радиуса - вектора r противоположны); если r<r0 (пружина сжата), сила - направлена от центра, и имеет знак «+» Рассмотренное поле сил представляет собой частный случай так называемого поля центральных сил, характерного тем, что направление силы, действующей в любой точке пространства, проходит через некоторый центр, а величина силы зависит только от расстояния до этого центра f=f(r)

Поле сил тяжести тоже является частным случаем центрального поля сил.

Приведенные примеры характерны тем, что силы, действующие на тело, зависят только от положения тела в пространстве (точнее, от положения тела по отношению к другим действующим на него телам) и не зависят от скорости тела.

Для сил, зависящих только от положения тела, может случиться, что работа, совершаемая ими над телом не зависит от пути, а определяется только начальным и конечным положениями тела в пространстве. В этом случае поле сил называется потенциальным, а сами силы — консервативными. Силы, работа которых зависит от пути, по которому тело переходит из одного положения в другое, называются неконсервативными.

Работа консервативных сил на любом замкнутом пути равна нулю. В самом деле, разобьем замкнутый путь» по которому совершает обход тело, находящееся в потенциальном поле, на две части: путь 1, по которому тело переходит из точки 1 в точку 2, и путь //, по которому тело переходит из точки 2 в точку 1 причем точки 1 и 2 выберем совершенно произвольно (рис, 57).

63

Рис. 57.	Рис. 58.
Работа на всем замкнутом пути будет равна сумме работ, совершаемых на каждом из
участков:
A = (A12 )I + (A21 )If .	(26.2)

Покажем, что работа, совершаемая на каком-либо пути, например на пути ΙΙ (рис. 57), при переходе тела по нему из точки 1 в точку 2 равна взятой с обратным знаком работе, совершаемой на том же пути при обратном переходе из точки 2 в точку 1. Рассмотрим участок траектории s (рис. 58). Поскольку в потенциальном поле сила f зависит только от положения тела в пространстве и не зависит от состояния движения тела (в частности, от направления

движения), элементарная работа на пути s при движении в одном направлении равна	A=f	s,
при движении же в другом направлении она равна A' = f s ' . Так как s ' = − s , то	A' = −	A .
Это справедливо для любого элементарного участка пути, а, следовательно, и для работы на
всем пути, так что
(A21 )If = −(A12 )If	(26.3)
Воспользовавшись полученным результатом, равенство (26.2) можно записать следующим
образом:
A = (A12 )I − (A12 )If .	(26.4)

Но в потенциальном поле сил работа не зависят от пути, т. е. (A12)1=(A12)11. Следовательно, выражение (26.4) равно пулю, что и требовалось доказать.

Если работа каких-то сил на любом замкнутом пути равна нулю, то работа этих сил при переходе тела из одного положения в другое; очевидно, не зависит от пути (это можно доказать, обратив ход проведенных выше рассуждений). Поэтому потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути равна нулю. Поскольку работа в потенциальном поле сил на замкнутом пути равна нулю, на одних участках замкнутого пути силы совершают положительную работу, а на других — отрицательную. Работа сил трения за промежуток времени t согласно (24.10) равна

A = fv t = − f υ t,

так как векторы fuv все время имеют противоположные направления1. Следовательно, работа сил трения все время остается отрицательной и на замкнутом пути будет отлична от нуля. Таким образом, силы трения принадлежат к числу неконсервативных сил.

1 Здесь имеется в виду случай трения между движущимся телом и неподвижными (относительно системы отсчёта) телами. В некоторых случаях работа силы трения может оказаться положительной. Это бывает, например , тогда , когда сила трения обусловлена взаимодействием данного тела с другим , движущимся в том же направлении но с большей скоростью.

64

Докажем, что поле сил тяжести является потенциальным. Сила, действующая на тело в любой точке траектории, имеет одинаковую величину P=mg и направление - вниз по вертикали (рис. 59). Поэтому согласно (24.12) работа равна:

A = P(h1 − h2 ) = mg(h1 − h2 )(26.5)

Рис. 59.

Это выражение, очевидно, не зависит от пути, откуда следует, что поле сил тяжести потенциально.

Поле центральных сил также потенциально. Элементарная работа на пути s (рис. 60) равна: A=f(r) sf

Рис. 60.

Но проекция s на направление силы в данном месте, т. е. на направление радиуса-вектора r равна r — приращению расстояния тела от точки О: sf= r. Поэтому

	A=f(r) r
Работа на всем пути
A = ∑	r = r	r2
	Ai = lim ∑2 f (ri )	ri = ∫ f (r)dr
	ri →0 r = r1	r
		1

Последнее выражение зависит, очевидно, только от вида функции f(r) и от значений r1 иr2. От ряда траектории оно никак не зависит, поэтому центральное поле сил тоже потенциально.

§27. Энергия. Закон сохранения энергии

Как показывает опыт, тела часто оказываются в состоянии совершать работу над другими телами. Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией. Энергия тела может быть обусловлена причинами двоякого рода: во-первых, движением тела с некоторой скоростью и, во-вторых, нахождением тела в потенциальном поле сил. Энергия первого вида называется кинетической энергией. Энергия

65

второго вида называется потенциальной энергией. Кратко можно сказать, что кинетическая энергия — это энергия движения, а потенциальная — энергия положения.

Кинетическая энергия. Пусть тело 1 (имеется в виду материальная точка) массы m, движущееся со скоростью v, действует на соприкасающееся с ним тело 2 с силой f (рис. 61),

Рис. 61.

За время dt точка приложения силы получит перемещение ds=vdt, вследствие чего тело 1 совершит над телом 2 работу:

dA = fds = fvdt.

(27.1)

Очевидно, что в данном случае тело 1 совершает работу над другим телом за счет запаса энергии, которой оно обладает в силу своего движения, т. е. за счет запаса кинетической энергии T (если бы тело 1 не двигалось, было бы равно нулю перемещение ds а следовательно, и работа dA). Поэтому совершенную телом 1 работу можно приравнять убыли1 его кинетической энергии:

dA = −dT.

Приняв во внимание (27.1), найдем, что
dT = − fvdt.	(27.2)

По третьему закону Ньютона тело 2 действует на тело 1 с силой F=—f, вследствие чего скорость тела 1 получает за время dt приращение

dv =	1		f 'dt = −	1	fdt.
		m		m
Умножив скалярно обе части последнего равенства на mv, найдем, что
	mvdv = − fvdt.				(27.3)

Сравнивая (27.3) с (27.2), получим выражение для dT:

	dT = mvdv	(27.4)
Согласно формуле (24.8) скалярное произведение vdv можно представить в виде
υ | dv | cosα = υ (dv)	2, где — dvnpu проекция вектора dv на направление вектора V.
npu

Из рис. 62 легко заключить, что (dv)npu равна приращению модуля скорости, т. е, dv. Поэтому выражение (27.4) можно записать следующим образом;

1 Изменение какой-либо величины, а можно характеризовать либо ее приращением, либо убылью

Приращением величины a, которое мы будем обозначать, а называют разность конечного (a2) и начального (a1) значений этой величины:

приращение= а=а2-а1

Убылью величины a называют разность её начального (a1) и конечного (a2) значений: убыль=а1-а2=- а.

Убыль величины равна её приращению с обратным знаком.

Приращение и убыль — алгебраические величины. Если а2>a1, приращение положительно, а убыль отрицательна. В случае, когда a2<a1 приращение отрицательно, а убыль положительна.

2 Нельзя писать это выражение в виде υ dυ cosα ,так как, вообще говоря,| dv | . ≠ dυ .

66

Рис.62

	dT = mυdυ = d			mυ 2		.	(27.5)
				2
	Отсюда следует1, что кинетическая энергия материальной точки массы m, движущейся со
	скоростью υ , равна
	T =	mυ 2		.			(27.6)
		2
	Умножив на m числитель υ знаменатель выражения (27.6) и приняв во внимание, что
	произведение mυ равно импульсу тела p , выражению для кинетической энергии можно
	придать вид
	T =		p2	.			(27.7)
			2m

Отметим весьма важное обстоятельство: работа A' совершаемая над телом, равна приращению его кинетической энергии T=T2-T1. Чтобы доказать это, напишем выражение для элементарной работы

dA' = f 'vdt

(f — сила, совершающая над телом работу, v — скорость тела). Теперь заменим произведение f 'dt через dp=mdv в результате получим

dA' =	mυ 2			= dT.
	f 'vdt = mvdv = mυdυ = d	2
Проинтегрировав это выражение, придем к формуле
	A' = T2 − T1.			(27.8)

Из (27.8) следует, что энергия имеет такую же размерность, как и работа. Это дает возможность измерять, энергию, в тех же единицах, какие используются для измерения работы.

Потенциальная энергия. Рассмотрим тело (имеется в виду материальная точка), находящееся в потенциальном, поле сил. Сопоставим каждой точке поля (характеризуемой радиус-вектором r) определенное значение некоторой функции U(r). осуществив это следующим образом. Для некоторой исходной точки 0 примем произвольное значение функции равное U0. Чтобы получить значение функции U1 в некоторой точке 1, прибавим к U0 работу A10, которую совершают над телом силы поля при перемещении тела из точки 1 в точку 0:

U1 = U0 + A10

(27.9)

		T =	mυ 2	+ const.
	1 Интегрирование уравнения (27.5) приводит к выражению		2
				Однако из физических

соображений ясно, что при υ = 0 кинетическая энергия T также равна нулю, откуда следует, что константу можно положить равной нулю.

67

(отметим, что определенная таким образом функция V имеет размерность работы или энергии). Поскольку работа в потенциальном поле сил не зависит от пути (см. §26), найденное таким способом значение U1 оказывается однозначным.

Аналогично определяются значения U(r) для всех остальных точек поля. В частности, значение U(r) в точке 2 равно

U2 = U0 + A20.

(27.10)

Вычислим разность U1-U2. Для этого вычтем из (27.9) выражение (27.10) и воспользуемся тем, что A20=-A02. В результате получим:

U1 − U2 = (U0 + A10 ) − (U0 + A20 ) = A10 − A20 = A10 + A02.

Но сумма A10 + A02 дает работу, совершаемую силами поли при перемещении тела из точки 1 в точку 2 по траектории, проходящей через точку 0. Однако работа, совершаемая над телом при его перемещении из точки 1 в точку 2 по любой другой траектории (в том числе и не проходящей через точку 0), будет такой же самой. Поэтому сумму A10+A02 можно записать просто в виде A12. В итоге мы придем к соотношению:

U1 − U2 = A12.

(27.11)

Таким образом, с помощью функции U(r) можно определить работу, совершаемую над телом силами поля на любом пути, начинающемся в произвольной точке 1 и заканчивающемся; в произвольной точке 2. Эта работа оказывается равной убыли функции U(r) на пути 1—2. Последнее обстоятельство дает основание трактовать физическую величину U(r) как один из видов механической энергии, который назвали потенциальной энергией.

Вследствие произвольности значения U0 [cм. формулу (27.9)] потенциальная энергия оказывается определенной с точностью до некоторой неизвестной аддитивной по стоянной. Это обстоятельство, однако, не имеет никакого значения, так как во все физические соотношения входит только разность значений C в двух положениях тела. Практически уславливаются считать U какого-то определенного положения тела равной нулю, а энергию других положений брать по отношению к этой энергии.

Конкретный вид функции U(r) зависит от характера силового поля. Так, например, в поле сил тяжести вблизи земной поверхности потенциальная энергия тела массы m имеет вид:

U = mgh

(27.12)

где h — высота, отсчитанная от уровня, для которого принято U = 0 . Это следует непосредственно из формулы (26.5), определяющей работу сил тяжести при перемещении тела с уровня h1 на уровень h2.

Поскольку начало отсчета U можно выбирать произвольно, потенциальная энергия может иметь отрицательные значения. Если, например, принять за нуль потенциальную энергию тела, находящегося на поверхности Земли, то потенциальная энергия тела, лежащего на дне ямы

глубиной h ' , будет равна U = −mgh ' (рис. 63), Отметим, что кинетическая энергия не может быть отрицательной.

В рассмотренном выше примере потенциальную энергию U=mgh мы относили к телу, находящемуся в поле сил тяжести, однако, строго говоря, потенциальную энергию следует относить к системе взаимодействующих друг с другом тел. Так, в разобранном случае

68

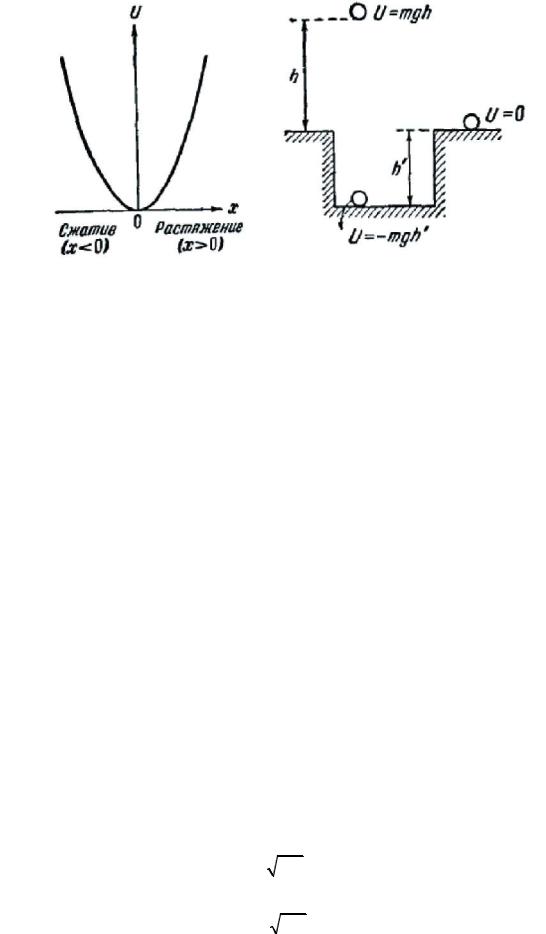
Рис. 63.

Рис. 64.

U=mgh есть энергия системы Земля — тело. Потенциальная энергия системы тел зависит от их расположения по отношению друг к другу.

Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая или растянутая пружина). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).

Согласно (24.5) как для сжатия, так и для растяжения пружины на величину x необходимо

затратить работу A =1 /2 kx2	. Эта работа идет на увеличение потенциальной энергии пружины.
Следовательно, зависимость потенциальной энергии пружины U от удлинения x имеет
следующий вид:
	U = kx2 .	(27.13)
	2

На рис. 64 эта зависимость показана графически.

Полная механическая энергия системы тел. В общем случае тело может обладать одновременно и кинетической и потенциальной энергией. Сумма этих энергий образует полную механическую энергию. Так, например, тело M, находящееся на высоте h над поверхностью Земли и движущееся относительно Земли со скоростью υ , обладает полной энергией:

E = mυ 2	+ mgh.	(27.14)
2

Точнее говоря, выражение дает полную энергию системы Земля — тело; mgh есть взаимная

потенциальная энергия этой системы, mυ 2 энергия Земли в рассматриваемой системе об энергии (27.14) как об энергии тела M.

/ 2 — кинетическая энергия тела M а кинетическая отсчета равна нулю, что и дает основание говорить

Потенциальная и кинетическая энергии могут превращаться друг в друга. Рассмотрим случай свободного падения первоначально покоившегося тела с высоты h. До начала падения кинетическая энергия тела равна нулю (тело покоится), а потенциальная — равна mgh. В конце падения тело обладает скоростью:

υ = 2gh

(27.15)

и, следовательно, кинетической энергии:

T = mυ	2		m (	2gh )	2
		=				= mgh,
				2
2

69

но зато потенциальная энергия на высоте h=0 будет равна нулю. Таким образом, потенциальная энергия превращается в эквивалентное количество кинетической энергии.

Тело, брошенное с поверхности Земли вертикально вверх со скоростью υ обладает вначале

кинетической энергией mυ 2 / 2 и потенциальной энергией, равной нулю. Постепенно теряя скорость, тело сможет подняться на высоту h, связанную с начальной скоростью соотношением (27.15). На высоте h скорость, а, следовательно, и кинетическая энергия тела, станет равной нулю, но зато его потенциальная энергия станет равной первоначальному запасу кинетической энергии.

В обоих случаях (падения и подъема тела вблизи поверхности Земли) полная энергия тела остается неизменной (сопротивлением воздуха движению тела пренебрегаем). Легко убедиться1

в том, что на любой про межуточной высоте h '(0 < h ' < h) сумма

mυ '2 + mgh ' 2

mυ 2

(υ ' — скорость на высоте h ' ) равна mgh или 2 .

Этот результат получился потому, что тело находилось под действием только силы, обусловливающей наличие потенциальной энергии (сила mg есть внутренняя сила, действующая в системе Земля—тело). Иначе обстоит дело при наличии внешних сил. За счет работы, совершаемой этими силами над телами, образующими систему, будет происходить изменение полной энергии системы. Пусть, например, первоначально покоившееся на поверхности Земли тело M окажется под действием силы f, большей силы тяжести mg и имеющей направление вверх по вертикали (эта сила может исходить только от тел, не входящих в систему Земля — тело М). Тогда тело начнет подниматься с некоторым ускорением, вследствие чего его потенциальная и кинетическая энергии будут расти, причем увеличение полной энергии будет равно работе, совершаемой над телом М внешней силой f.

Полная механическая энергия системы, состоящей из N тел, между которыми действуют консервативные силы, слагается из потенциальной энергии системы как целого и из кинетической энергии системы, которая в свою очередь слагается из кинетических энергий отдельных тел, образующих систему:

	N	mυ 2
	E = U + T = U + ∑	i i	.	(27.16)
		2
	i=1

Закон сохранения энергии. Рассмотрим систему из N тел, между которыми действуют только консервативные силы (рис. 65).

1 Рекомендуется проделать это в порядке упражнения.

70

Рис.65

Предположим, что тело 1 переместилось по произвольной траектории в положение 1. При этом силы, с которыми действуют на тело 1 все остальные тела системы, совершат работу, не зависящую от пути перемещения тела 1 и определяющуюся лишь начальным и конечным положениями тела относительно всех других тел. Аналогично при перемещении всех N тел в новые положения над этими телами консервативные силы, действующие в системе, совершат работу, величина которой зависит только от начального и конечного расположения тел друг относительно друга. Следовательно, каждому взаимному расположению (каждой конфигурации) тел можно приписать определенное значение потенциальной энергии U, и работу консервативных сил при переходе от одной конфигурации к другой вычислять как разность значений U, соответствующих этим конфигурациям:

A12 = U1 −U2.

(27.17)

Пусть на тела системы, кроме консервативных внутренних сил, действуют также внешние силы. Работу, совершаемую всеми силами, приложенными к i-му телу системы, можно представить как сумму работы (A12)i совершаемой внутренними силами, и работы Ai совершаемой внешними силами, действующими на данное тело. Полная работа идет, как мы знаем, на приращение кинетической энергии тела [см. (27.8)]. Следовательно,

( A12 )i + A'i = (T2 )i − (T1 )i .	(27.18)
суммируя выражение (27.18) по всем телам системы, получим:
∑( A12 )i + ∑ A'i = ∑(T2 )i − ∑(T1 )i	(27.19)

Первая из сумм в выражении (27.19) представляет собой работу консервативных сил, совершаемую над телами при переходе системы из начальной (первой) конфигурации в конечную (вторую). Согласно (27.17) эта работа может быть представлена как разность значений потенциальной энергии системы в начале и в конце процесса:

∑(A12 )i = U1 − U2 .

Вторая сумма в левой части выражения (27.10) представляет собой полную работу внешних сил, совершаемую над телами системы. Обозначим ее A'

Правая часть в (27.19), очевидно, равна, T2-T1, т. е. разности значений полной кинетической энергии системы в конечном и начальном состояниях.

Таким образом, формуле (27.19) можно придать вид

U1 − U2 + A' = T2 − T1.

71