v		>		x		(β + β 2	− ω 2 ).
	0				0			0

§74. Автоколебания

При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту убыль энергии, колебания станут незатухающими. Пополнение энергии системы может осуществляться за счет толчков извне, одна ко эти толчки должны сообщаться системе В такт с ее колебания ми, в противном случае они могут ослабить колебания и даже прекратить их совсем. Можно сделать так, чтобы колеблющаяся система сама управляла внешним воздействием, обеспечивая согласованность сообщаемых ей толчков со своим движением. Такая система называется автоколебательной» а совершие незатухающие колебания — автоколебаниям и.

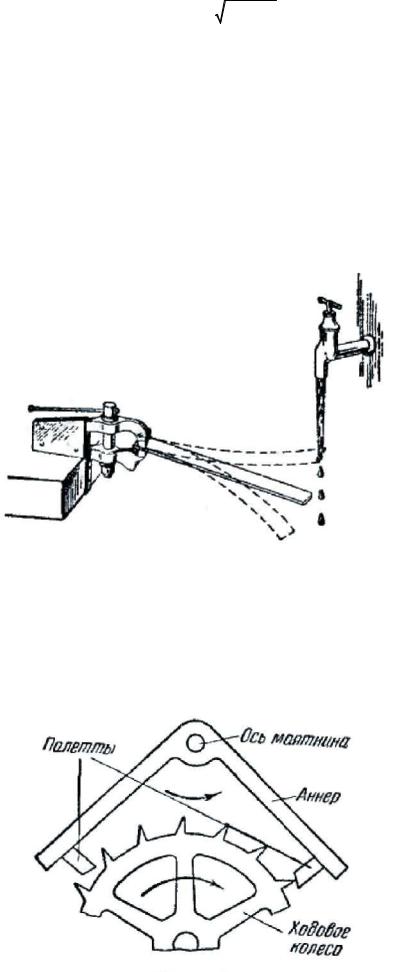
В качестве одной из простейших автоколебательных систем рассмотрим устройство, изображенное на рис. 185. Гибкая упругая линейка зажата одним концом неподвижно. Если оттянуть свободный конец линейки

Рис. 185

затухающие колебания. Колебания можно сделать незатухающими, направив на конец линейки струйку воды так, чтобы струйка задевала линейку в тот момент, когда она находится в верхнем крайнем положении. Удары струйки о конец линейки восполняют убыль энергии колебаний, обусловленную трением.

В качестве второго примера автоколебательной системы рассмотрим часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом — анкером (рис. 186).

188

Рис. 186

На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо упирается одним из зубьев в боковую поверхность той либо иной палетты, скользящей при качании маятника по поверхности зуба. Только в моменты, когда маятник находится вблизи среднего положения, палетты перестают преграждать путь зубьям и ходовое колесо проворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качаний маятника (за период) ходовое колесо проворачивается на два зуба, причем каждая из палетт получает по толчку. Через посредство этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения.

§75. Вынужденные колебания

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (мы будем называть ее вынуждающей силой). Пусть вынуждающая сила изменяется со временем по гармоническому закону

f = F0 cosωt.

(75.1)

При составлении уравнения движения нужно учесть, кроме вынуждающей силы, также те силы, которые действуют в системе при свободных колебаниях, т, е. квазиупругую силу и силу сопротивления среды. Предполагая колебания достаточно малыми, будем по-прежнему считать силу сопротивления пропорциональной скорости. Тогда уравнение движения запишется следующим образом

mx = −kx − rx + F0 cosωt.

Разделив это уравнение на m и перенеся члены с х и x х в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:

				x + 2β x + ω02 x = f0 cosωt,			(75.2)
где f0 =	F0	, β =	r	— коэффициент затухания, ω0 =	k	собственная частота колебаний
	m		2m		m

системы.

Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем [см. функцию (73.10), являющуюся общим решением уравнения (73.2)]. Оно имеет вид

x = a0e− β t cos(ω 't + α '),

(75.3)

где ω ' = ω02 − β 2 , a0,α ' — произвольные постоянные. Остается найти частное (не содержащее

произвольных постоянных) решение уравнения (75.2), Предположим, что это решение имеет вид

x = a cos(ωt − ϕ )

(75.4)

(в данном случае удобно обозначить начальную фазу вместо а через —ϕ ). С помощью

векторной диаграммы (см. §68 и 69) легко убедиться в том, что наше предположение справедливо, а также определить значения а и (р, при которых функция (75.4) удовлетворяет уравнению (75.2). Дифференцируя (75.4) по времени, первые два члена уравнения (75.2) можно представить в следующем виде:

2βx = −2βωa sin(ωt − ϕ ) = 2βωa cos	ωt − ϕ +	π ,	(75.5)
		2

189

x = −ω 2a cos(ωt − ϕ ) = ω 2a cos(ωt − ϕ + π ).

(75.6)

Как следует из (75.2), гармоническое колебание f0 cosωt является суммой трех гармонических колебаний той же частоты: колебания (75.6), колебания (75.5) и колебания ω02 x = ω02a cos(ωt − ϕ ). Если изобразить последнее колебание вектором длины ω02a , направленным

a)	б)
	Рис. 187.
вправо (рис. 187), то колебание (75.5) изобразится вектором длины 2βωa , повернутым

относительно вектора ω02 x против часовой стрелки на угол π / 2, а колебание (75.6) —

вектором длины ω 2a повернутым относительно вектора ω02 x на угол π . Чтобы уравнение

	(75.2) было удовлетворено, векторная сумма перечисленных трех векторов должна совпадать с
	вектором, изображающим колебание f0 cosωt . Такое совпадение возможно лишь при
	значении амплитуды я, которое определяется условием (см, рис. 187, а)
	(ω02 − ω 2 )2 a2 + 4β 2ω 2a2 = f02
	откуда
	a =	f02	.	(75.7)
		(ω02 − ω 2 )2
			+ 4β 2ω 2

Рис. 187, а отвечает случаю ω < ω0 . Из рис. 187, 6, соответствующего случаюω > ω0 получается такое же значение а.

Рис. 187 позволяет получить также и значение ϕ , которое представляет собой величину

отставания по фазе вынужденного колебания (75.4) от обусловившей его вынуждающей силы (75.1). Из рисунка следует, что

	tgϕ =	2βω	(75.8)
		ω02 − ω 2

Подставив в (75.4) значения а и ϕ определяемые формулами (75.7) и (75.8), получим частное решение неоднородного уравнения (75.2):

190

		f0				2βω
x =					ωt − arctg				(75.9)
	(ω02	2		cos		2		2 .
		− ω 2 )	+ 4β 2ω 2			ω0	− ω

Функция (75.9) в сумме с (75.3) дает общее решение уравнения (75.2), описывающее поведение системы при вынужденных колебаниях. Слагаемое (75.3) играет заметную роль только в начальной стадии процесса, при так называемом установлении колебаний (рис. 188)

Рис. 188.

С течением времени из-за экспоненциального множителя e− βt роль слагаемого (75.3) все больше уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (75.9).

Таким образом, функция (75.9) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (75.7) вынужденных колебаний пропорциональна амплитуде вынуждающей силы.

Для данной колебательной системы (определенных ω0 и β ) амплитуда зависит от частоты

вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания ϕ так же зависит от частоты вынуждающей силы [см. (75.8)].

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому» что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения, Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота — резонансной частотой.

Чтобы определить резонансную частоту ω рез, нужно найти максимум функции (75.7) или,

что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по ω и приравняв нулю, мы получим условие,

определяющее ω рез:

− 4(ω02 − ω 2 )ω + 8β 2ω = 0.

(75.10)

Уравнение (75.10) имеет три решения: ω = 0 и ω = ± ω02 − 2β 2 . Решение равное

кулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение:

191

ω рез = ω02 − 2β 2 .

(75.11)

Подставив это значение частоты в (75.7), получим выражение для амплитуды при резонансе:

	a рез =	f0	.	(75.12)
		ω02
	2β		− β 2

Из (75.12) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (75.11) резонансная частота при тех же условиях

(при β = 0) совпадает с собственной частотой колебаний системы ω0 .

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же caмое, от частоты колебаний) показана графически па рис, 189. Отдельные кривые на

графике соответствуют различным значениям параметра β . В соответствии с (75.11) и (75.12), чем меньше β , тем выше и правее лежит максимум данной кривой. При очень большом

затухании (таком, что 2β 2 > ω02 ) выражение для резонансной частоты становится мнимым.

Это означает, что при этих условиях резонанс не наблюдается — с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 189). Изображенная на

Рис. 189.

рис. 189 совокупность графиков функции (75.7), соответствующих различным значениям параметра β , называется резонансными кривыми.

По поводу резонансных кривых можно сделать еще следующие замечания. При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному

значению, равному f0 /ω02 , т. е. F0/k. Это значение представляет собой смещение из

положения равновесия, которое получает система под действием постоянной силы величины F0. При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно

сместиться из положения равновесия. Наконец, отметим, что чем меньше β , тем сильнее изменяется c частотой амплитуда вблизи резонанса, тем «острее» получается максимум.

192

Из формулы (75.12) вытекает, что при малом затухании (т. е. при β << ω0 ) амплитуда при резонансе приближенно равна

aрез ≈	f0	.
	2βω0

Разделим это выражение на смещение xq из положения равновесия иод действием

постоянной силы F0, равное, как мы выяснили,						f0 /ω02 . В результате получим:
	aрез	≈	ω	0	=	2π	=	π	= Q
	x					2βT		λ
			2β
0

[см. формулу (73.13)]. Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).

Рис. 190.

Как видно из рис. 187, вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания ϕ лежит в пределах от 0 до ϕ . Зависимость ϕ от ω при разных

значениях β показана графически на рис. 190. Частоте соответствует ϕ = π / 2. Резонансная частота меньше собственной [см. (75.11)]. Следовательно, в момент резонансаϕ < π / 2 . При слабом затухании ω рез ≈ ω0 , 0 значение ϕ при резонансе, можно считать равным π / 2.

С явлением резонанса приходится считаться при конструировании машин и различного рода сооружении. Собственная частота колебании этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае возникают вибрации, которые могут вызвать катастрофу. Известны случаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебаний моста оказывалась близкой к частоте с которой шагала колонна.

193