− μgh

p = Ce RT

Подставив сюда h=0 получаем

p0 = C

где ро—давление на высоте h=0.

Таким образом, при сделанном нами допущении о постоянстве температуры зависимость давления от высоты выражается формулой

p = p0e−	μgh	(108.4)
	RT

Эта формула называется барометрической. Из нее следует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура.

Рис. 245

На рис. 245 изображены две кривые вида (108.4), которые можно трактовать либо как соответствующие разным μ (при одинаковой T), либо как отвечающие разным T (при одинаковой μ).

§109. Распределение Больцмана

Заменив в (108.4) давление р через kT [см, (99.12)], получим закон изменения с высотой числа молекул в единице объема:

− μgh

n = n0e RT

Здесь nо—числе молекул в единице объема на высоте, равной нулю, n — то же число на высоте h.

Полученное выражение можно преобразовать, заменив отношение μ/R равным ему отношением m/r где m — масса одной молекулы, r—постоянная Больцмана:

n = n0e−	μgh	(109.1)
	RT

Из (109.1) следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает, обращаясь в нуль при Т=0 (рис. 246). При абсолютном нуле все молекулы расположились бы на земной поверхности. При высоких температурах, напротив, n слабо убывает с высотой, так что молекулы оказываются распределен наши по высоте почти равномерно.

Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате

272

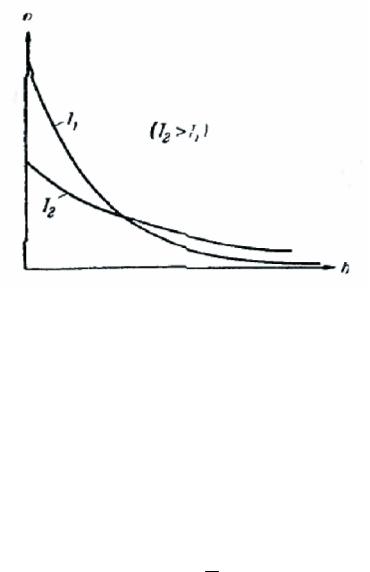
Рис 246

действия двух тенденций: 1) притяжение молекул к земле (характеризуемое силой mg) стремится расположить их на поверхности земли; 2) тепловое движение (характеризуемое величиной kТ) стремится разбросать молекулы равномерно по всем высотам. Чем, больше m и меньше Т, тем сильнее преобладает первая тенденция и молекулы сгущаются у поверхности земли. В пределе при Т=0 тепловое движение совсем прекращается и под влияния притяжения молекулы располагаются на земной поверхности. При высоких температурах превалирует тепловое движение и плотность молекул медленно убывает с высотой.

На разной высоте молекула обладает различным запасом потенциальной энергии:
ε p = mgh	(109.2)

Следовательно, распределение (109.1) молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. С учетом (109.2) формулу (109.1) можно записать следующим образом:

ε p
n = n0e− rT	(109.3)

где n0 — число молекул в единице объема в том месте, где потенциальная энергия молекулы равна нулю, n - число молекул в единице объема, соответствующее тем точкам пространства,

где потенциальная энергия молекулы равна ε p .

Из (109.3) следует, что молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия, и, наоборт, с меньшей плотностью в местах, где их потенциальная энергия больше.

В соответствии с (109.3) отношение n1 и n2 в точках, где потенциальная энергия молекулы имеет значения ε p1 и ε p2 , равно

	n1	= e	−	ε p1 − e p2
				kT	.	(109.4)
	n
	2

Больцман доказал, что распределение (109.3), как и вытекающая из него формула (109.4), справедливо не только в случае потенциального поля сил земного тяготения но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В соответствии с этим распределение (109-3) называют распределением Больцмана.

В то время как закон Максвелла дает распределение частиц по значениям кинетической энергии, закон Больцмана дает распределение частиц по значениям потенциальной энергии.

273

Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение кинетической или соответственно потенциальной энергии одной молекулы к величине, определяющей среднюю энергию теплового движения молекулы.

Распределении (106.14) и (109.3) можно объединить в один закон Максвелла — Больцмана, согласно которому содержащееся в единице объема количество молекул, скорость которых

лежит между υ и υ + dυ , равно

3

e p +

mυ 2

E

m

2

−

2

−

(109.5)

= n

2

dυ ≈ e

2

dn

4π

e

kT υ

kTυ

dυ,

e p,υ

0

2πkT

где nо— число молекул в единице объема в той точке, в которой ε p = 0, а E — полная энергия

молекулы, равная сумме ее кинетической и потенциальной энергий.

В соответствии с условием (106.5) интегрирование (109.5) по и в пределах от 0 до со

− e p

приводит к выражению n = n0e kT , совпадающему с распределением (109.3).

В распределении (109.5) потенциальная энергия ε p и кинетическая энергия mv2/2, а

следовательно и полная энергия E, могут принимать непрерывный ряд значений. Если полная энергия частицы может принимать лишь дискретный ряд значении: E1, E2, .., как это имеет место, например, для внутренней энергии атома, то распределение Больцмана имеет вид:

	−	Ei				(109.6)
	N i= Ae kT .
	где Ni — число частиц, находящихся в состоянии с энергией Еi, А — коэффициент
	пропорциональности, который должен удовлетворять условию
	∑ Ni = A∑e−		Ei
			kT		= N
	(N—полное число частиц в рассматриваемой системе).

Подставив найденное из последнего соотношения значение А в формулу (109.6), получим окончательное выражение распределения Больцмана для случая дискретных значений энергий:

			Ne−	Ei
N		=		kT				.
	i
			∑e−		Ei
					kT

§110. Определение Перреном числа Авогадро

Распределение (109.4) было положено Перреном (1909 гг) в основу опытов по определению числа Авогадро. Взвешенные в жидкости очень мелкие твердые частицы находятся в состоянии непрестанного беспорядочного движения, называемого броуновским движенцем (см. §91).

Причина его заключается в том, что при достаточно малых размерах частиц импульсы, сообщаемые частице ударяющимися о нее с разных сторон молекулами, оказываются некомпенсированным и. О частицу заметных размеров ударяется одновременно большое число молекул, так что суммарный результат ударов молекул достаточно хорошо усредняется. При малых размерах частицы начинают проявляться отклонения скоростей отдельных молекул и числа ударяющихся молекул от средних значений. Если скорость или число молекул, ударяющихся о частицу с одной стороны, окажется иной, чем для молекул, ударяющихся с другой стороны, то результирующий импульс, сообщаемый частице, будет отличен от нуля и

274

частица начнет двигаться в соответствующем направлении. В следующий момент результирующий импульс имеет иное направление. Следовательно, частица будет все время перемещаться беспорядочным образом.

Броуновское движение указывает на то, что достаточно малые частицы вовлекаются в совершаемое молекулами тепловое движение. Принимая участие в тепловом движении, такие частицы должны вести себя подобно гигантским молекулам, и на них должны распространяться закономерности кинетической теории, в частности закон (109.4).

Основную трудность в опытах Перена составляло приготовления одинаковых частиц и определение их массы. Применив многократно метод центрифугирования, Перрену удалось приготовить весьма однородную эмульсию из практически одинаковых шариков гуммигута1 с радиусами порядка нескольких десятых долей микрона. Эмульсия помешалась в плоскую стеклянную кювету глубиной 0,1 мм и рассматривалась с помощью микроскопа (рис. 247).

Рис. 247.

Микроскоп имел столь малую глубину поля зрения, что в него были видны только частицы, находящиеся в горизонтальном слое толщиной примерно 1 мк. Перемещая микроскоп в вертикальном направлении, можно было исследовать распределение броуновских частиц по высоте.

Обозначим высоту слоя, видимого в микроскоп, над дном кюветы буквой h. Число частиц, попадающих в поле зрения микроскопа, определяется формулой

N = n(h)S h

где n0—число броуновских частиц в единице объема на высоте h, S — площадь, a ∆h — глубина поля зрений микроскопа.

Применив к броуновским частицам формулу (109.3), можно написать:

n(h) = n e−	p′h
	kT	,
0

где по — число частиц в единице объема при h=0, p’ — вес броуновской частицы в эмульсии, т. е. вес, взятый с учетом поправки на закон Архимеда.

Написав выражение числа частиц ∆N для двух разных высот h1 и h2 получаем:

− p′h1

N1 = n0e kT S h,

− p′h2

N2 = n0e kT S h.

Наконец, логарифмируя отношение ∆N1/∆N2, приходим к следующему выражению:

1 Гуммигут — сгущенный млечный сок, получаемый из надрезов в коре некоторых видов деревьев, растущих в Ост-Индии и на Цейлоне

275