dA		=	dAx
				dt
		dt прx
	dA		=	dAy
				dt
		dt прy
	dA		=	dAz
				dt
		dt прz

,

, (2.11)

.

Нужно быть очень аккуратным в обозначениях. Так, например, проекцию вектора dA/dt на

dA

ось х нельзя обозначить символом dt x , потому что такой символ по

аналогии с Ах будет означать составляющую вектора dA/dt по оси х. Нельзя также обозначать

dA

эту проекцию символом

dt x

(подобно обозначению проекции вектора А символом Ах), так

dA

вообще говоря, отличен от

dA

. Поэтому приходится прибегать к обозначениям вида

как

dt

dt

dA

dt прx

и т. д.

§3. Скорость

Положение материальной точки (в дальнейшем для краткости мы будем говорить просто точки) в пространстве можно задать с помощью радиуса-вектора r.

При движении точки вектор r изменяется, вообще говоря, и по величине, и по направлению1.

Зафиксируем некоторый момент времени t. Ему соответствует значение г радиуса-вектора

(рис. 16).

Рис.16

В течение следующего за моментом t небольшого промежутка времени ∆t (мы будем называть его элементарным) точка проходит элементарный путь ∆s и получает элементарное перемещение ∆r, которое совпадает с приращением радиуса-вектора за время ∆t2.

1Рекомендуется в порядке упражнения указать траекторию, для которой радиус-вектор точки изменяется: а) только по величине, б) только по направлению

2Символом ∆ (дельта) мы будем пользоваться в двух случаях: Символом ∆ (дельта) мы будем пользоваться в двух случаях:

16

Образуем отношение

r

(3.1)

t

При данном t модуль и направление вектора (3.1), вообще говоря, зависят от величины промежутка ∆t. Станем уменьшать ∆t (соответственно будут также уменьшаться ∆s и ∆r), наблюдая при этом за поведением отношения (3.1). Оказывается, что по достижении достаточно малых значений ∆t вектор (3.1) практически перестает изменяться как по величине, так и по направлению. Это означает, что при стремлении ∆t к нулю отношение (3.1) стремится к определенному пределу. Этот предел называется скоростью v движущейся точки в момент времени t. Символически сказанное выше записывается следующим образом:

v = lim	r	(3.2)
t→0	t

Итак, скоростью называется предел, к которому стремится отношение ∆r к ∆t при неограниченном убывании ∆t. Следовательно, скорость можно определить как производную радиуса-вектора движущейся точки по времени:

v = dr	(3.3)
dt

Как следует из ее определения, скорость есть величина векторная.

Рис.17

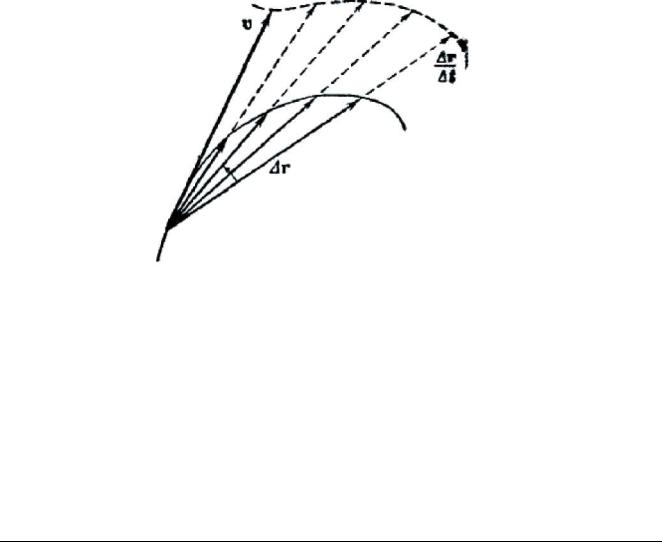
Из рис. 17 видно, что вектор ∆r/∆t является секущей для траектории. При предельном переходе (3.2) точки пересечения этого вектора с траекторией все более сближаются (∆s стремится к нулю), сливаясь в конечном итоге в одну точку, вследствие чего секущая превращается в касательную. Таким образом, вектор скорости оказывается направленным по касательной к траектории в соответствующей точке (рис. 18).

В соответствии с формулой (3.2) модуль вектора скорости может быть записан следующим образом:

υ =

v

=

lim

r

= lim

r

(3.4)

t

t

t→0

t→0

В этом выражении нельзя вместо |∆r| писать ∆r. Символ |∆r| означает модуль приращения сектора r,

a)для обозначения доли какой-либо величины. Например, в рассматриваемом случае ∆t есть часть всего времени в течение которого происходит движение, ∆s — часть всего пути, проходимого точкой;

b)для обозначения приращения какой-либо величины. В данном случае ∆r есть приращение радиуса-вектора r за время ∆t

17

Рис.18

Рис.19

в то время как ∆r представляет собой приращение модуля вектора r: ∆|r|. Обе эти величины не равны друг другу:

r ≠ r = r

В этом можно убедиться на следующем примере (рис. 19). Пусть некоторый вектор А получает такое приращение ∆А, что модуль его не изменяется;

A + A = A

Следовательно, приращение модуля вектора А равно нулю (∆|А|=∆A=0). В то же время модуль приращения вектора |∆A| отличен от нуля (он равен длине отрезка 2 — 3). Рис. 20 поясняет, что при данном |∆А| приращение модуля ∆|А| может иметь значение в пределах от —

|∆А| до +|∆А

Рис.20

Элементарный путь ∆s, вообще говоря, отличен по величине от модуля элементарного перемещения |∆r| (рис 21).

Рис.21

Однако, если брать отрезки пути ∆s и перемещения ∆r, соответствующие небольшим промежутка у времени ∆t, то различие между ∆s и |∆r| будет невелико, причем при уменьшения ∆t путь ∆s с возрастающей точностью будет совпадать с |∆r|. Па этом основании можно написать, что

18

	lim	r	= lim	s
		t		t
	t→0		t→0

откуда в соответствии с (3.4) для модули скорости получается следующая формула:

υ = lim	s	= ds	(3.5)
t→0	t	dt

§4. Вычисление пройденного пути

Из выражения (3.5) следует, что при малых ∆t

	υ	s	(4.1)
		t

Последнее приближенное равенство выполняется тем точнее, чем меньше ∆t. Если известна величина скорости v как функция времени t, можно вычислить путь, пройденный точкой с момента t1 до момента t2. Для этого разобьем промежуток времени t1-t2 на N малых промежутков: ∆t1, ∆t2, …, ∆tN, которые могут быть различными по величине. Весь путь s, пройденный точкой, можно представить как сумму путей: ∆s1, ∆s2, …, ∆sN пройденных за соответствующие промежутки времени ∆t;

	N
s = s1 + s2	+ ...+ sN = ∑ si	1
	i=1

В соответствии с (4.1) каждое из слагаемых ∆sі (і — любое число от 1 до N) может быть приближенно представлено в виде

si υi ti

где ∆tі — промежуток времени, за который был пройден ∆sі, a vi — одно из значений скорости за время ∆tі. Таким образом,

N
s ∑υi		ti	(4.2)
i =1
Написанное равенство выполняется тем точнее, чем меньше промежутки времени. В
пределе при стремлении всех ∆tі к нулю (количество промежутков ∆tі будет при этом
неограниченно возрастать) сумма, стоящая справа, станет точно равна s:
s = limt →0	N
	∑υi	ti	(4.3)
i	i=1

Скорость есть функция времени: υ=υ(t). В математике выражения вида:

N

limx 0 ∑ f (xi ) xi

i → i=1

составленное для значений х, заключенных в пределах от а до b, называют определенным интегралом и записывают символически следующим образом;

∫b f (x)dx

a

Следовательно, путь, пройденный точкой за промежуток времени от t1 до t2 равен определенному интегралу

	t2		(	)	(4.4)
s =	∫	υ
				t dt
	t1

1 Так принято записывать сумму N слагаемых одинакового вида.

19