§10. Кинематика вращательного движения

Все точки абсолютно твердого тела, вращающегося вокруг некоторой оси ОО (рис. 29),

Рис. 29.

движутся по окружностям, центры которых лежат на оси вращения. Радиус-вектор каждой точки (вектор, проведенный из центра соответствующей окружности в данную точку) поворачивается за время t на один и тот же угол Δφ - угол поворота твердого тела.

Поворот тела на некоторый угол φ можно задать в виде отрезка, длина которого равна φ, а направление совпадает с осью, вокруг которой совершен поворот. Для того чтобы указать, в какую сторону совершается поворот вокруг данной оси, можно условиться связывать направления поворота и изображающего его отрезка так называемым правилом правого винта. Согласно этому правилу направление отрезка должно быть таким, чтобы, глядя вдоль него (рис. 30),

Рис. 30.

мы видели поворот совершающимся по часовой стрелке (вращая головку правого винта по часовой стрелке, мы вызовем его перемещение от себя). Таким образом, повороту тела можно приписать численное значение и направление. Однако этого еще недостаточно для того, чтобы поворот можно было считать вектором, — нужно, чтобы изображаемые таким способом повороты складывались по правилу параллелограмма. Для поворотов произвольной величины последнее условие не выполняется. Покажем это на примере вращения сферы (рис. 31). Поворот сферы вокруг оси 1 — 1 на угол π/2 (этот поворот изображен отрезком ϕ1 ) и

следующий за ним поворот вокруг оси 2 — 2 на π/2 (отрезок ϕ2 ) приводят к тому, что точка А

28

перемещается сначала в положение A′ , а затем в положение А". Поворот, который изображается полученным из ϕ1 и ϕ2 по правилу параллелограмма отрезком ϕ3 (этот отрезок

имеет длину π 2 ), переводит точку А в положение B, не

Рис. 31.

совпадающее с A". Следовательно, поворот, изображаемый отрезком φ3, вовсе не равнозначен поворотам φ1 и φ2, совершаемым один за другим, и поэтому не является их суммой. Таким образом, мы убедились в том, что, хотя поворот тела вокруг оси можно изобразить направленным отрезком, его нельзя считать вектором.

Иначе обстоит дело для очень малых углов поворота Δφ. Путь, проходимый любой точкой тела при очень малом повороте, можно считать прямолинейным. Два совершаемых последовательно малых поворота Δϕ1 и Δϕ2 обусловливают, как видно из рис. 32 такое же

29

Рис. 32.

перемещение r1 + r2 любой точки тела, как и поворот φ3, получаемый из ϕ1 и ϕ2 по

правилу параллелограмма. Отсюда следует, что очень малые повороты могут рассматриваться как векторы (мы будем их записывать в виде Δφ или dφ).

Направление вектора dφ мы определили, связав его определенным образом с направлением вращения тела. При рассмотрении таких величин, как скорость v, ускорение w, радиус-вектор r не возникал вопрос о выборе их направления: оно вытекало естественным образом из природы самих величин. Подобные векторы называются полярными. Векторы типа dφ, направление которых связывается с направлением вращения (или обхода), называют аксиальными векторами.

Векторная величина

ω = lim	Δϕ	= dϕ	(10.1)
t→0	t	dt

(где t — время, за которое совершается поворот Δφ) называется угловой скоростью тела1. Вектор ω направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 33), и представляет собой аксиальный вектор.

1 Чтобы отличить рассмотренную нами ранее скорость v oт угловой скорости, ее называют линейной. В дальнейшем в случаях, когда это не сможет привести к недоразумениям, слово «линейная» мы будем опускать.

30

	Рис. 33.
	Модуль вектора угловой скорости равен	dϕ		. Вращение с постоянной угловой скоростью
		dt
	называется равномерным, при этом ω=φ/t. Таким образом, при равномерном вращении ω
	показывает, на какой угол поворачивается тело за единицу времени.
	Равномерное вращение можно характеризовать периодом обращения T, под которым
	понимают время, за которое тело делает один оборот, т, е. поворачивается на угол 2π.
	Поскольку промежутку времени t=T соответствует угол поворота Δφ=2π,
		ω =			2π			(10.2)
					T
	откуда
		T =			2π			(10.3)
					ω
	Число оборотов в единицу времени v, очевидно, равно
	ν =		1		=	ω		(10.4)
			T			2π

Из (10.4) следует, что угловая скорость равна 2π, умноженным на число оборотов в единицу

времени:
ω = 2πν	(10.5)

Понятия периода обращения и числа оборотов в единицу времени можно сохранить и для неравномерного вращения, понимая под мгновенным значением Т то время, зa которое тело совершило бы один оборот, если бы оно вращалось равномерно с данным мгновенным значением угловой скорости, а под ν понимая то число оборотов, которое совершало бы тело за единицу времени при аналогичных условиях.

Вектор ω может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется по величине), так и за счет поворота оси вращения в пространстве (в этом случае ω изменяется по направлению). Пусть за время t вектор ω получает приращение Δω. Изменение вектора угловой скорости со временем характеризуется величиной

β = lim	Δω	= dω	(10.6)
t→0	t	dt

которую называют угловым ускорением. Вектор β, как и ω, является аксиальным. 31

Когда направление оси вращения в пространстве остается постоянным, угловая скорость изменяется только по величине и | Δω |=| Δω | . В этом случае из (10.6) получается следующее

	выражение для модуля углового ускорения:
	β = lim	| Δω |	=		dω
							(10.7)
		t			dt
	t→0

Если под β понимать проекцию вектора β на направление ω, то формула (10.7) запишется следующим образом:

β = lim	Δω	= dω	(10.8)
t→0	t	dt

В формуле (10.8) β—алгебраическая величина, которая положительна, если ω со временем увеличивается (о этом случае векторы β и ω имеют одинаковое направление), и отрицательна, если ω уменьшается (в этом случае направления β и ω противоположны).

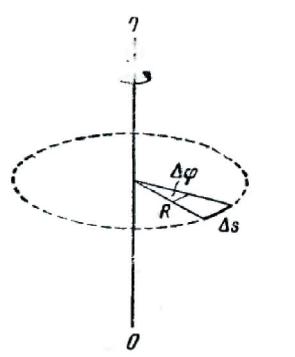
Отдельные точки вращающегося тела имеют различные линейные скорости v. Скорость каждой из точек, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости υ определяется скоростью вращения тела ω и расстоянием R рассматриваемой точки от оси вращения, пусть за малый промежуток времени t тело повернулось на угол Δφ (рис. 34).

Рис 34.

Точка, находящаяся на расстоянии R от оси, проходит при этом путь s, равный

s = R ϕ

Линейная скорость точки по определению будет равна
υ = lim	s	= lim R	Δϕ	= R lim	Δϕ	= R dϕ	= Rω,
t→0	t	t→0	t	t→0	t	dt
т.е.
			υ = ωR				(10.9)

Итак, чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она движется.

Найдем линейное ускорение точек вращающегося тела. Нормальное ускорение согласно

(9.4) равно

32