Смысл этого признака в том, что если мы домножим подынтегральную функцию на что-то, похожее на константу, то интеграл этого произведения по-прежнему будет сходиться.

Прежде чем пойти дальше, стоит взглянуть на следующий пример. Исследуем на сходимость интеграл от функции

( ) = {

12 ,

R Q.

1

,

Q,

2

−

Для

+∞

> 0

+∞

+∞

2

∫

| ( )| =

∫

любого

интеграл

сходится. Тогда по следствию 42.6 должен

сходится и

∫

( ) . Однако это не так. Дело в

том, что данная функция не интегрируема на

+∞

любом конечном отрезке [ , ]. А значит, определить

∫

( ) вообще нельзя. Поэтому важно

помнить, как именно определяется несобственный интеграл, чтобы не допустить ошибки.

Часть 43

Приложения интегрального исчисления к вычислению площадей

1Многоугольные фигуры

Будем называть многоугольной фигурой объединение конечного числа многоугольников. Понятие многоугольной фигуры, таким образом, допускает несвязность этой фигуры (например, два отдельных многоугольника). Плоской фигурой будем называть ограниченное множество точек на плоскости (т.е. все эти точки можно поместить внутрь какого-то круга).

Обозначим площадь многоугольной фигуры как ( ). Мы будем считать по определению, что ( ) > 0.

Многоугольные фигуры и называются равными, если существует взаимно однозначное отображение, сохраняющее расстояние между точками, переводящее в . Иными словами, эти две фигуры совпадают при наложении друг на друга.

1.1Свойства площади

1.Инвариантность. Равные фигуры имеют равные площади.

2.Аддитивность. Если многоугольные фигуры и не имеют общих внутренних точек, то ( ) = ( ) + ( ).

3.Существование единицы. Площадь квадрата со стороной единичной длины равна единице площади.

2Квадрируемость фигуры

Рассмотрим — произвольную плоскую фигуру. Пусть — произвольная многоугольная фигура, лежащая внутри , а — некоторая многоугольная фигура, содержащая в себе .

129

Тогда выполняется

( ) 6 ( ) 6 ( ).

Множество { ( )} ограничено сверху (например, любой ( )), значит sup{ ( )} = .

Эту величину назовем нижней площадью. Аналогично, множество { ( )} ограничено снизу

(например, нулем), а значит inf { ( )} = . Эту величину назовем верхней площадью.

Проще говоря, мы оцениваем площадь данной фигуры с помощью описанной и вписанной многоугольных фигур, площади которых мы легко можем находить.

Плоская фигура называется квадрируемой (имеющей площадь), если = = . За площадь мы и примем это . Площадь плоской фигуры удовлетворяет тем же свойствам, что и площадь многоугольной фигуры. Однако с некоторыми выводами стоит быть осторожнее. Например, можно обобщить свойство аддитивности на конечное число фигур. Если 1, . . . , — квадрируемые фигуры, не имеющие общих внутренних точек, то

	( =1 )	=	=1 ( ).
			∑

Но, вообще говоря, это свойство не выполняется для счетного числа фигур. Но перед тем как привести контрпример, введем еще одно понятие. Будем говорить, что имеет нулевую площадь, если может быть вписано в многоугольную фигуру сколь угодно малой площади.

Теперь рассмотрим множество = [0,1]×[0,1] — все точки, имеющие рациональные координаты в единичном квадрате. Поскольку у каждой точки нулевая площадь, то = 0. С другой стороны, в любой окрестности любой точки этого квадрата есть точки с рациональными координатами, а значит, чтобы их все покрыть, нужно взять весь квадрат целиком. Т.е. = 1. А значит, не является квадрируемой.

3Критерии квадрируемости

Здесь читателю предлагается вспомнить понятие границы множества (стр. 71).

Теорема 43.1 (Критерий I). квадрируема т.и.т.т., когда ее граница имеет нулевую площадь.

Теорема 43.2 (Критерий II). квадрируема т.и.т.т., когда существуют последователь-

ности квадрируемых фигур { }, { }, такие	что	и ,	и	lim ( ) =
lim ( ).				→∞
→∞

4Криволинейная трапеция

Познакомимся теперь с важным классом квадрируемых фигур. Рассмотрим непрерывную на отрезке [ , ] функцию ( ), такую что [ , ]

( ) > 0. Тогда криволинейной трапецией называется фигура = {( , ) R2 | 6 6 , 0 6 6

( )}. Пример такой фигуры проиллюстрирован на рисунке справа.

130

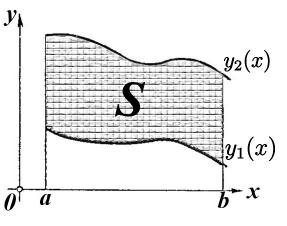
Теорема 43.3. Криволинейная трапеция является квадрируемой фигурой с площадью

( ) = ∫
	( ) .

Доказательство. Для начала отметим, что раз ( ) непрерывна на [ , ], то она и интегрируема на нем. Рассмотрим теперь = { } =0 — произвольное разбиение отрезка [ , ].

Пусть

= inf

( ), а = sup

( ). Теперь определим следующие фигуры:

[ −1, ]

[ −1, ]

* =

[ −1, ] × [0, ],

=1

* =

[ −1, ] × [0, ].

=1

Таким образом,

*

лежит внутри этой трапеции, а * покрывает ее. По определению этих

фигур (

)

6

( )

6

заметим, что (

) =

∑

— не что иное,

( *). Но теперь

*

*

=1

как нижняя сумма Дарбу, а ( *) =

— верхняя сумма Дарбу. Но тогда, вспоминая

=1

один из критериев интегрируемости

по Риману (стр. 112), получаем то, что и требовалось

∑

доказать.

[:|||||:]

Следствие 43.4. Если функция ( ) является отрицательной, то ее площадь, лежащая под осью абсцисс, берется с противоположным знаком.

∫

Следствие 43.5. Если = {( , ) | 6 6 , 1( ) 6 6 2( )}, то ( ) = ( 2( )− 1( )) .

Наконец, рассмотрим фигуру = {( , ) | 6 6 , 0 6 6 ( )}. Ее площадь считается

аналогично, только теперь мы берем интеграл по : ( ) = ∫	( ) .

5Параметрически заданная кривая

Рассмотрим теперь фигуру, заданную функцией {	= ( )	[ 0, ], а ( ), ( ) —
	= ( ) , где
непрерывно дифференцируемые на [ 0, ] функции.

131

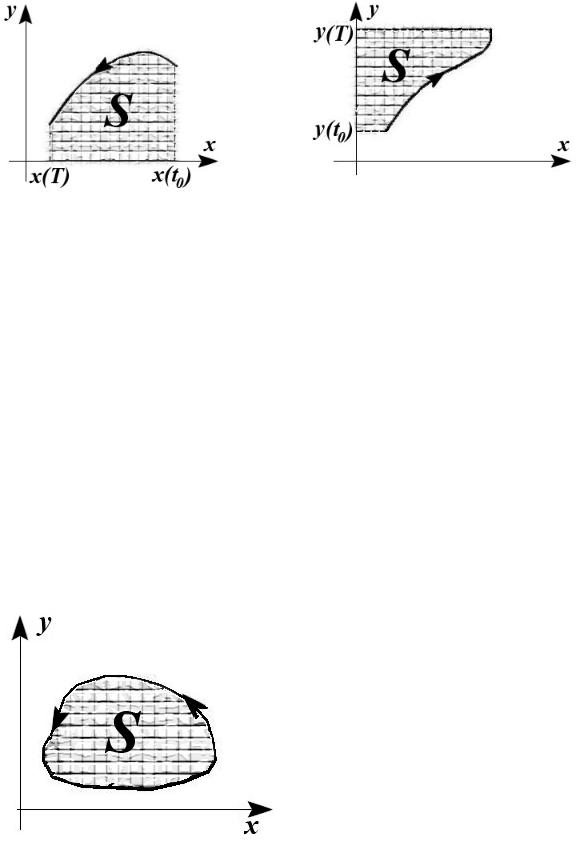
Назовем положительным обходом такой обход кривой, при котором рассматриваемая область остается слева (на рисунках ниже показан именно этот порядок). Порядок обхода очень важен для корректного перехода от представленных выше простых формул к параметрическим.

Но пока рассмотрим незамкнутую кривую. В этом случае можно считать площадь фигуры, «двигаясь» как по , так и по .

Можно записать
= ′( )	= ( )	= ( 0),
= ′( )	= ( 0)	= ( ).

Тогда получаем две практически эквивалентные формулы:

( ) = − ∫	( ) ′( ) ,
0
∫

( ) = ( ) ′( ) .

0

Если же замкнута (проиллюстрировано ниже), то

( ) = 2		( ( ) ′( ) − ( ) ′( )) = 2		( ( ))2	( ( )).
	∫0		∫0
1		1				( )

Впрочем, все три формулы можно применять как для замкнутых, так и для незамкнутых кривых. Несмотря на то, что последняя формула является простой композицией первых двух, применять ее иногда удобнее. Например, для кривой, заданной как ( ) = cos , ( ) = sin .

132