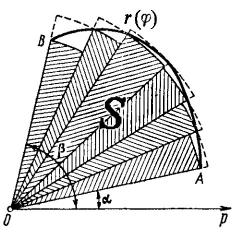
6Площадь фигуры в полярной системе координат

Научимся находить площадь фигуры = {( , ) | 0 6 6 ( ), < < }, т.е. заданной в полярной системе координат. Здесь ( ) — непрерывная функция.

Рассмотрим произвольное разбиение = 0 < 1 < · · · < = . Определим следующие

величины:
=	inf	( ),
	−16 6
=	sup	( ),
	−16 6
* =
	{( , ) | 0 6 6 , −1 < < },
	=1
* =	{( , ) | 0 6 6 , −1 < < }.
	=1

Геометрический смысл этих величин продемонстрирован на рисунке: — это сектор, который целиком содержится внутри данного участка под кривой, а — сектор, покрывающий этот участок. А фигуры * и * соответственно построены из этих секторов. Тогда выполняется

( *) 6 ( ) 6 ( *). Но

		1			2
( *) = ∑						,
		2
	=1
( *) =			1	2		.
	∑
		2
	=1

А это не что иное, как нижняя и верхняя суммы Дарбу. А значит при диаметре разбиения,

стремящемся к 0, данные суммы сходятся к одному и тому же числу: 12 ∫ 2( ) . Значит,

( ) =	2		2( ) .
		∫
	1

133

Часть 44

Вычисление длины дуги кривой и объема тела вращения

1Понятие кривой на плоскости и в пространстве

Пусть в R3 задана прямоугольная декартова система координат. Множество точек Γ = {( ( ); ( ); ( )) | [ , ]}, где ( ), ( ), ( ) — непрерывные на [ , ] функции, называется непрерывной кривой (кривой Жордана). Для удобства будем обозначать ¯( ) радиус-вектор с координатами ( ( ); ( ); ( )), а ^( ) точку с координатами ( ( ); ( ); ( )). Тогда можно записать Γ = {^( ) | [ , ]}.

Точка кривой Γ называется точкой самопересечения (кратной), если 1 ̸= 2 : ^( 1) =

^( 2) = . Кривую, у которой нет кратных точек, назовем простой. Если ^( ) = ^( ), то кривая называется замкнутой (контуром).

Кривая Γ = {^( ) | [ , ]} называется дифференцируемой (непрерывно дифференцируемой), если дифференцируема (непрерывно дифференцируема) ¯( ). Ориентация кривой, отвечающая увеличению параметра , называется положительной, в противном случае — отри-

цательной.			< · · · <
Рассмотрим некоторое разбиение	= 0	< 1		= . Соединим точки ^( −1) и
^( ) отрезками прямой. В результате	получим ломаную Λ . При этом выполняется				ΛΓ	=
			Γ

∑

|¯( ) − ¯( −1)|. Здесь ΛΓ обозначает длину. Это обозначение ( ) будем использовать и в

=1

дальнейшем.

Назовем кривую Γ спрямляемой (имеющей длину), если sup ΛΓ = Γ < ∞. Что го-

ворится в этом определении? Увеличивая число отрезков, которыми соединяются точки на кривой, мы точнее можем посчитать длину данной кривой. Устремляя диаметр разбиения к 0, мы фактически покрываем кривую бесконечным количеством маленьких отрезочков. Если это удалось сделать, значит длину кривой можно посчитать, и она как раз равна сумме длин этих отрезочков.

Лемма 44.1 (Аналог теоремы Лагранжа для вектор-функции). Пусть вектор-функция

¯ = ¯( ) непрерывна на сегменте [ , ] и дифференцируема на интервале ( , ). Тогда

( , ):

|¯( ) − ¯( )| 6 |¯′( )|( − ).

Доказательство. Если ¯( ) = ¯( ), то все доказано. Если ¯( ) ̸= ¯( ), то положим

¯ = ¯( ) − ¯( ) . |¯( ) − ¯( )|

Получаем, что |¯| = 1. Тогда

|¯( ) − ¯( )| = (¯( ) − ¯( ), ¯) = (¯( ), ¯) − (¯( ), ¯).

	Введем функцию одного переменного ( ) = (¯( ), ¯), для которой выполнены все условия
теоремы Лагранжа. Следовательно, ( , ) такое, что:
	|¯( ) − ¯( )| = ( ) − ( ) = ′( )( − ) = (¯′( ), ¯)( − ) 6 |¯′( )|( − ).
1.	Последний переход сделан, используя неравенство Коши-Буняковского и тот факт, что |¯| =
	[:|||||:]

134

Теорема 44.2. Если кривая Γ непрерывно дифференцируема, то она спрямляема и |¯( ) −

¯( )| 6 Γ 6 max |¯′( )|( − ).

[ , ]

Доказательство. Можно записать (первый переход выполнен в соответствии с неравенством треугольника):

¯( )

¯( )

∑

sup

= sup

∑

¯( )

¯(

) .

|

−

| 6

|¯(

) − ¯( −1)| 6

ΛΓ

|

−

−1

|

=1

=1

По лемме 44.1

∑

∑

¯′( ) (

sup

−1

)

|

= sup

′

max

−

).

=1

|¯(

) − ¯(

|¯ (

)( −

−1)| 6

[ , ] |

|

=1

[:|||||:]

2Длина дуги кривой

Назовем точку кривой Γ, отвечающую значению параметра 0, особой, если ¯′( 0) = 0 или @¯′( 0). Непрерывно дифференцируемую кривую без особых точек будем называть гладкой. Определим также Γ — дугу кривой Γ = {^( ) | 6 6 } и ( ) — длину дуги Γ , отсчитываемую от = .

Теорема 44.3. Для гладкой кривой Γ функция ( ) является монотонно возрастающей,

причем

( )

=

= ( ′( ))2 + ( ′( ))2 + ( ′( ))2.

√

Доказательство. Рассмотрим

дугу

кривой,

отвечающую параметру ( 0, 0

+ ):

|

¯(

+

)

−

¯( )

| 6

(

)

max

|

¯′( )

|

,

0

0

0

6 [ 0, 0+Δ ]

|¯( 0 +

) − ¯( 0)|

( 0)

max

¯′( )

.

6

6 [ 0, 0+Δ ] |

|

Теперь перейдем к пределу при

→ 0:

( )

( )

0

6

0 6

|¯′( 0)|.

Но тогда +′ ( 0) =

¯′( 0) (т.к.

>

0) и,

аналогично,

′

( 0)

=

|

¯′( 0)

. Тогда

′( 0) =

|

|

−

|

|¯′( 0)| > 0, т.к. кривая Γ не имеет особых точек. А это и значит, что

( ) ↑.

[:|||||:]

Чтобы понять, зачем нужна данная теорема, сделаем хитрый ход. Нам нужно вычислить длину дуги кривой на отрезке [ , ], т.е. найти ( ). Можно записать ( ) = ( ) − 0 = ( ) −

( ) = ∫ ′( ) . А вот теперь можно воспользоваться только что доказанной теоремой:

( ) = ∫	′( ) = ∫	(¯′( )) = ∫
				( ′( ))2	+ ( ′( ))2 + ( ′( ))2 .
			√

135

В более простом случае, когда кривая задана как функция = ( ), и нужно найти длину дуги при 6 6 , можно воспользоваться следующей параметризацией:

{

= ∫ √

= 1 + ( ′( ))2 .

= ( )

Наконец, полезно знать формулу для расчета длины дуги, заданной в полярных координатах. Пусть кривая задана уравнением = ( ) ( 6 6 ), где ( ) — непрерывно дифференцируемая на [ , ] функция. Тогда длина соответствующего участка кривой равна

∫

√

= 2( ) + ( ′( ))2 .

3Объем тела вращения

Рассмотрим непрерывную и неотрицательную на [ , ] функцию = ( ). Давайте посчитаем объем тела, полученного вращением криволинейной трапеции, которую задает эта функция, вокруг оси , как показано на рисунке.

Возьмем произвольное разбиение : = 0 < 1 < · · · <= и введем следующие величины:

= sup ( ),

[ −1, ]

= inf ( ),

[ −1, ]

Ω* = [ −1, ] × { 2 + 2 6 2},

=1

Ω* = [ −1, ] × { 2 + 2 6 2}.

=1

Чтобы посчитать объем тела, мы действуем так же, как действовали при вычислении площади фигуры под графиком. Мы разбиваем данную фигуру на много-много цилиндров (неравенство 2 + 2 6 2 задает круг радиуса вокруг при фиксированном ). Затем ограничиваем одним объединением цилиндров (Ω*) фигуру сверху, а другим (Ω*) снизу, т.е. выполняется(Ω*) 6 6 (Ω*). Если теперь устремить диаметр разбиения к 0, то объемы обеих фигур сойдутся к искомому объему. А объем цилиндра мы легко можем находить:

		∑
(Ω*) =		2	,
		=1
*		∑
(Ω	) =		.
		=1

Фактически записаны нижняя и верхняя суммы Дарбу. Но тогда

→0	*	→0
			∫
lim (Ω		) = lim (Ω*) = =	2( ) .

136