12.1.4. Калибровочные симметрии

Действие Намбу — Гото очевидно инвариантно относительно замены координат, поскольку площадь является геометрическим инвариантом.

Инфинитезимальные замены координат приводят к следую­щим преобразованиям полей:

6Х^л = %_чХ^А = д1^ахХ, (12.1.4.1)

где 2_б£ — производная Ли по направлению двумерного вектора

-6|^а. Соотношение (12.1.4.1) отражает тот факт, что Х^А яв­ляются двумерными скалярами.

При преобразованиях полей Х^л по правилу (12.1.4.1) воз­никает следующая вариация лагранжиана:

_а

(12.1.4.2)

является двумерной плотностью). Следовательно, вариация действия сводится к интегралу по границе (линии):

(12.1.4.3)

и, конечно, равна нулю для тех преобразований координат, ко­торые на границе обращаются в нуль.

Квадратичное действие (12.1.2.1) также обладает инвари­антностью относительно замены координат, и преобразование метрики 7ссЗ имеет вид

_у. (12.1.4.4)

Кроме того, как мы уже видели, квадратичное действие так­же обладает вейлевской инвариантностью (преобразования <1216))

106 Глава 12

12.1.5. Глобальные симметрии

Струна распространяется в d-мерном пространстве-времени, которое является плоским, поэтому имеется пуанкаре-инвари-антность.

Симметрия по отношению к группе Пуанкаре в данном слу­чае похожа на внутреннюю симметрию (этот тип симметрии ха­рактерен для а-моделей), и она связывает преобразованием различные поля, взятые в одной и той же точке х^а:

Х^в, (12.1.5.1 а)

(выражения (12.1.5.1) не содержат производных).

Используя метод Нётер, получаем d{d-{- l)/2 сохраняю­щихся токов, удовлетворяющих уравнению непрерывности d_aj^a~Q. Это токи, соответствующие трансляциям:

, a

а также токи, отвечающие поворотом и бустам:

Пи, = -На = -^Г^х_В]--^г V=£ ^д_№Х_[АХ_В]. (12.1.5.3)

^ол, а

Заряды получаются интегрированием

л или 2л

Qa = S Рл<Ь (12.1.5.4)

О

(полный импульс струны) и

л или 2я

Qab= S i°AB^do (12.1.5.5)

О

(угловой момент).

В случае замкнутых струн заряды, очевидно, сохраняются вследствие уравнения непрерывности, так как в системе, в ко­торой нет границ, не может быть ни входящего, ни выходя­щего потока. В открытых струнах заряды сохраняются только в том случае, если выбрать подходящие граничные условия при а = 0 и а = я, которые запрещают поток через эти границы (см. разд. 12.1.7).

12,1.6. Конформная симметрия

Среди преобразований координат х^а^>х ^а = /^а(лг) есть такие„ при которых метрика умножается на локальный фактор. Эти

Струна Намбу — Гото: классический анализ 107

преобразования носят название псевдоконформных преобразо­ваний ¹):

^& являются конформными преобразованиями

^t

(12.1.6.1)

Инфинитезимальные конформные преобразования х'^а=х^а-\- $£" удовлетворяют условию

%tgat = *>g₄, (12.1.6.2)

как видно из разложения уравнения (12.1.6.1).

Чтобы проанализировать свойства конформной группы, удобно переписать уравнение (12.1.6.1) в "конформной калиб­ровке", т. е. в системе координат, в которой метрика пропорцио­нальна двумерному тензору Минковского:

(х) — ф² (х) гц («конформная калибровка») (12.1.6.3)

= V—ff Лае-

Существование таких систем координат хорошо известно из дифференциальной геометрии (см., например, книгу Эйзенхар-та [5] и разд. 12.5, где обсуждается калибровка светового ко­нуса).

Соотношение (12.1.6.3) позволяет записать уравнение (12.1.6.1) в виде

дх^а дх^ —

^Л2() (12.1.6.4)

что в инфинитезимальной форме эквивалентно уравнениям

б|⁰₀ = б?'„ 6|°, = 6i'_o (12.1.6.5)

(условия псевдо-Коши — Римана).

С этими уравнениями удобнее работать в светоподобных координатах (и, у), в которых квадрат длины записывается как ds² = —2<j»²dudv. Тогда конформные преобразования U{u,v), V(u_t v) являются преобразованиями координат, подчиненными

*) Очевидно, можно принять бескоордииатные обозначения и определить зконформиую группу, но здесь это необязательно, поскольку мы рассматриваем (по крайней мере в этом разделе) многообразия с тривиальной топологией {-^R²) и используем глобальные координаты.

108 Глава 12

условиям

ди ди

dU dV

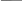
dv dv

==0, (12.1.6.6)

= 0. (12.1.6.7>

Следовательно, с точностью до перестановочного преобразова­ния U = v, V = u общее двумерное конформное преобразова­ние является прямым произведением двух одномерных коорди­натных преобразований

U = U{u), V = V(v). (12.1.6.8),

Соответственно конформная группа является прямым произве­дением двух групп одномерных диффеоморфизмов¹). Эта струк­тура прямого произведения оказывается явной в светоподоб-ных координатах.

В терминах координат Минковского х°, х¹ получаем

(12.1.6.9).

Новые координаты х'° и х^п удовлетворяют свободному волно­вому уравнению.

По многим причинам конформная группа играет важнуку роль в теории струн. Одна из причин заключается в том, что эта группа является остаточной группой диффеоморфизмов в. часто используемой конформной калибровке (12.1.6.3).

Более важным оказывается то свойство, что алгебра компо­нент тензора энергии-импульса скалярного поля X^х изоморфна конформной алгебре (ее центральное расширение называется алгеброй Вирасоро). Именно это свойство мы сейчас обсудим.

Рассмотрим безмассовое двумерное скалярное поле Х(х^а) с обычным действием

i^ ^ . (12.1.6.10)

Очевидно, это выражение инвариантно относительно преобра­зований координат из конформной группы.

По теореме Нётер эта инвариантность приводит к бесконеч­ному числу сохраняющихся токов, которые имеют вид

= 7"% (12.1.6.11)

где |Р —конформный вектор Киллинга, т. е. решение уравне­ния (12.1.6.2). Здесь Т^а$ — компоненты симметричного бесследо-

^]) В случае, если одномерное многообразие является окружностью, эта группа обозначается Diff{5¹).

Струна Намбу—Гото: классический анализ 109

вого тензора энергии-импульса скалярного поля (~b&fbgap> см. выражение (12.1.2.3)):

Т^ = 7^^а₉ Г^а0;_Р = О, Т\ = 0 (12.1.6.12)

(как мы уже говорили в разд. 12.1.2, бесследовость тензора 7^ар является результатом вейлевской инвариантности, а сим­вол ";" обозначает ковариантную производную).

Используя соотношения (12.1.6.12) и условие (12.1.6.2) для конформного вектора Киллинга, действительно можно убедить­ся, что ток /^а(£) сохраняется:

/^а(1)_;а = 0. (12.1.6.13)

Соответствующие заряды определяются выражением

\^, (12.1.6.14)

где интегрирование ведется по пространственной кривой. Из общих соображений следует, что заряды Q(g), выраженные в виде функций в фазовом пространстве от X и сопряженного импульса, удовлетворяют скобкам Пуассона, соответствующим конформной алгебре:

Ю(Ю, Q(ti)] = Q(E. л]). (12.1.6.15)

Здесь [|, т|] — конформный вектор Киллинга, полученный взя­тием скобок Ли от векторов g и rj:

_{R, чГ = rftf - l4V (12.1.6.16)}

Ниже мы явными вычислениями получим соотношение (12.1.6.15), которое означает просто, что алгебра симметрии реализуется в фазовом пространстве через скобки Пуассона. Чтобы перейти от соотношения (12.1.6.15) к скобкам Пуас­сона для компонент тензора энергии-импульса, возьмем кон­кретный вектор 1^а. Например, если в момент времени х°~0

векторы |^а и ц^а взять в виде

	(12.1.6.	17а)
= 0	(12.1.6.	176)
что	заряды	сво-

|°(0, *i) = fi (я¹ - а), 140,

(в координатах Минковского), то получим, дятся к

Q(6) = rg(a), Q(r,) = r°o(aO, (12.1.6.18)

и алгебра (12.1.6.15) даст скобки Пуассона [Го((т), Го (сг')]-Чтобы вычислить компоненты скобок Ли (12.1.6.16), нужно проинтегрировать конформные уравнения Киллинга для |^а и ц^а

НО Глава 12

с приведенными выше начальными условиями (12.1.6.17). Это дает

л _xi) ₌ ^ _{[б (л;}о _{+ x}i _ _{ff) + 6 {х}о __x

, (12.1.6.19)

°, х¹) = -L [б (*° + х¹ - а) - 6 (*° - х¹ + а)].

Аналогичные выражения получаются и для г\^а, (Конечно, ос­новной факт здесь заключается в том, что векторы £^а, т]^а пол­ностью определяются из начальных условий (12.1.6.17) и кон­формных уравнений Киллинга. Без этого алгебра (12.1.6.15) была бы бессмысленной, поскольку она связывала бы выраже­ние, хорошо определенное на поверхности jc° = O (в левой ча­сти алгебры) с выражением, содержащим векторы g^a и ц^а вне поверхности а'° = 0 (в правой части). Этим свойством конформ­ной группы полная группа диффеоморфизмов не обладает.) Скобки Ли векторов £^а и ц^а имеют следующий вид:

[I, т|]°(0, *■) = <>,

В, Л]¹ (0, х¹) = -fi (х¹ - а) 6' (х¹ - о') + б (х¹ - а') б' (*' - а),

(12.1.6.20)

где штрихом обозначена обычная пространственная производ­ная. Следовательно, скобки Пуассона при совпадающем вре­мени имеют вид

(а), Г_оо(а')] = (Г₀₁ (а) + Т₀₁ (а')) б^ (а - </)• (12.1.6.21 а) Аналогично получаем

Foo W. ^Го! (стО1 = (Уоо (ст) + ^оо И) б' (а - а'), (12.1.6.216)

(а), Г_ш (а⁷)] - (Г₀₁ (а) + Г₀₁ (а')) б' (а - а'). (12.1.6.21в)

На этом мы завершаем вычисления алгебры, которой удов­летворяют компоненты тензора энергии-импульса. Это та же самая конформная алгебра, записанная в базисе "векторов-б-функций". (Близкие вопросы обсуждаются в работе Фубини и др. [8], а также в цитируемой там литературе.)

Все рассмотренное здесь для случая безмассового скаляр­ного поля остается справедливым и для струны, описываемой d такими полями. Так как конформная группа является теперь подгруппой общей калибровочной группы теории, ее генераторы должны быть равны нулю. Но остается то важное свойство, что компоненты тензора энергии-импульса и в этом случае удовлет­воряют конформной алгебре.

Струна Намбу — Гото: классический анализ Ш

Упражнения

1а. Покажите, что из (12.1.6.4) следуют соотношения

Z — zZ , Z =&Z _y 8=1,

для инфинитезимальных конформных преобразоваиий х'^а = = 2^а(л^). Выведите, что произвольное конформное преобразо­вание является произведением пространственного отражения Z⁰ — х°, Z¹ = —х¹ и некоторого преобразования, удовлетворяю­щего условиям псевдо-Кошн—Римана.

16. Покажите сходство двумерных переменных светового конуса и, v, использованных в псевдоконформной группе, и комплексных переменных z,z — x±:iy, применяемых в евкли­довой конформной группе.

2а. Покажите, что условие бесследовости 7^а_а = 0 в свето-подобных переменных записывается, как T^uv = 0.

26. Покажите, что закон сохранения тензора энергии-им­пульса означает, что Т^ии является функцией только v, тогда как T^vv является функцией только и: Т^ии ~T^ua(v)_t T^Vv = T^vv(u).