12.1.7. Граничные условия

В случае замкнутых струн уравнений движения

= 0, (12.1.7.1а)

_р = 0 (12.1.7.16)

достаточно для того, чтобы действие (12.1.2.1) было экстре­мальным на классической траектории. Для открытых струн это неверно. В этом случае действие достигает экстремума, только если уравнения движения (12.1.7.1) удовлетворяются вместе с подходящими граничными условиями при о —0 и п. Эти гра­ничные условия необходимы для того, чтобы нежелательные граничные члены, возникающие в вариации действия S, обра­щались в нуль.

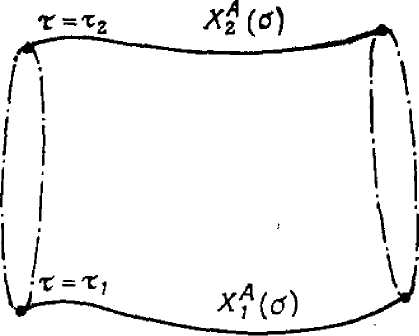
Пусть Х\ (а) и Х₂ (о) — две конфигурации открытой струны в моменты времени xi и т₂ соответственно. Мы хотим найти экстремум действия в классе всех траекторий струны Х⁴(т, а),

которые начинаются из Xf (а) в момент времени п и заканчи­ваются в Х$ (о) в момент времени тг- Мы не требуем, чтобы функции Х^А (т, а) имели заданные значения на вертикальных линиях а = 0 и а === я, следовательно, мы допускаем произволь­ные значения вариаций 6Х^А(%,0) и &Х^А(%, л). Две возможные эволюции струны изображены на рис. 12.1.

Причина, по которой мы различаем временные и простран­ственные границы, заключается в том, что мы рассматриваем

112 , Глава 12

Рис. 12.1. В вариационной задаче для открытой струны траектории концов струны Х^А(т, 0) и Х^А{х, я) также варьируются.

в данном случае струны со свободными концами. Принцип дей­ствия должен полностью определять движение струны в буду­щем, и мы не должны доопределять это движение дополнитель­ной внешней информацией. Чтобы импульс и угловой момент струны сохранялись, необходимо отсутствие взаимодействий с внешним миром через границы.

Мы вычислим вариацию действия для произвольных вариа­ций полей, удовлетворяющих приведенным выше требованиям. Для простоты возьмем действие в квадратичной форме. Легко найти все члены в вариации действия:

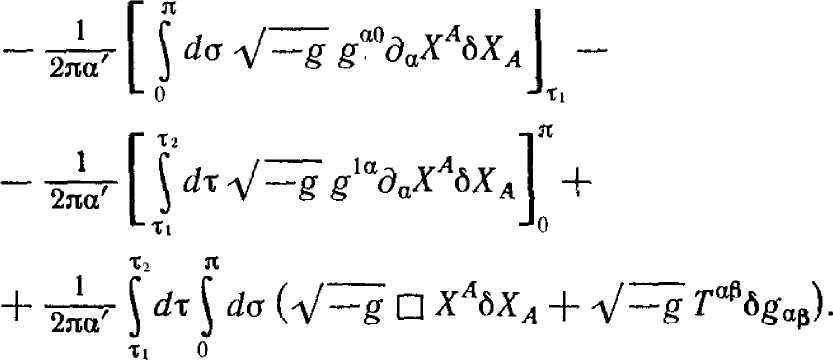(12.1.7.2)

Первый член в правой части равен нулю, так как струна

имеет фиксированные конфигурации Х\ (а) и Х2 (а) при tj и т₂. Требуя, чтобы и остальные члены в выражении для 6S были равны нулю для любых допустимых эволюции струны, мы по­лучим не только уравнения движения (12.1.7.1), но также условия

л/^И g^lad_aX^A = 0 при а = 0, я. (12.1.7.3)

Это и есть искомые граничные условия для случая открытых струн. (В случае замкнутых струн, конечно, нет пространствен­ной границы, поэтому не нужно накладывать условия (12Л.7.3), чтобы получить &S —С

Струна Намбу — Гото: классический анализ 113

Прежде чем обсуждать геометрический смысл соотношений (12.1.7.3), заметим, что граничные условия являются более фун­даментальными, чем уравнения массовой поверхности, как это можно видеть из приведенного выше вывода. В действительно­сти их нужно накладывать даже на поля вне массовой поверх­ности, чтобы иметь корректную вариационную задачу. В самом деле, для тех полевых траекторий, которые не удовлетворяют условиям (12.1.7.3), действие фактически является "недиффе-ренцируемым" в том смысле, что его вариация не представ­ляется в виде двумерного интеграла, содержащего только ва­риации полей без производных:

_{ьха+"йг6ga*)d% dc <12Л-7-4>}

(остаются граничные члены при 0 = 0 и я).

Поскольку мы умеем обращаться только с дифференцируе­мыми действиями (которые приводят к хорошо определенной канонической структуре), здесь и далее мы ограничимся про­странством траекторий открытых струн, удовлетворяющих ус­ловиям (12.1.7.3). Как мы уже показали, эти условия являются естественными граничными условиями для данного вариацион­ного принципа, так как они допускают произвольные вариации траекторий концов струны Х^л (т, 0) и Х^л (т, я) в вариационном принципе.

Геометрический смысл соотношений (12.1.7.3) мы сразу уви­дим, как только вспомним, что два d-мерных вектора дХ^А/дх и дХ^А/да, по предположению, являются линейно независимыми. Другими словами, если некоторая линейная комбинация этих двух векторов равна нулю, то коэффициенты в этой линейной комбинации также должны быть равны нулю. Поэтому условия (12.1.7.3) эквивалентны условию

V^i^-O, (12.1.7.5)

или, выражая g^la через

p==r==0==-^. (12.1.7.6)

V—g V—g

Таким образом, мы видим, что goo и g_Oi равны нулю на гра­ницах (ga$ и g по-прежнему остаются ограниченными функция­ми, как и скалярное произведение Минковского регулярных векторов), т. е. индуцированная метрика оказывается вырож­денной в граничных точках струны:

дХ^А дХ_Д дХ^А дХ

дт дт ~"

при о = 0, л. (12.1.7.7)

114 Глава 12

Более того, gu строго положительно, a g^ должно стремиться?

к нулю быстрее, чем g₀₀, поэтому отношения (12.1.7.6) в самом деле равны нулю:

g-u > 0, (12.1.7.8а>

- ^л- (12.1.7.86)

(Если g²_Ql ~ g₀₀ или g₀₀ < gj_p то £₀₁/ V~£ не стремится к нулю.

в граничных точках.)

Первое равенство (12.1.7.7) выражает тот факт, что вектор дХ^л/дх является светоподобным. Второе равенство (12.1.7.7) означает, что вектор дХ^А/дт также ортогонален пространствен­ному вектору, касательному к мировой поверхности струны. Таким образом, мы видим, что концы струны движутся со ско­ростью света под прямым углом к струне; траектория струны касательна к изотропным плоскостям в граничных точках.

Нужно отметить, что вырождение метрики в граничных точ­ках на первый взгляд противоречит выбору конформной ка­либровки (g₀₀ —0, g_пф0 не согласуется с выбором g_a& = ~Ф²Ца$). Но это противоречие не является серьезным; оно об­суждается ниже (противоречие снимается, если использовать подходящим образом выбранные координаты, в которых дХ^А/да = 0 при а = 0, л).

Физическое объяснение этого особого движения концов струны состоит в следующем. Струна движется свободно, по­этому ее угловой момент (вызванный движением концов стру­ны под прямым углом к струне) должен уравновешивать внут­реннее натяжение, которое стремится стянуть ее в точку. С уче­том рассмотренных граничных условий эффективное натяжение струны обращается в нуль в точках сг = О, я [9]. В то же время граничные условия означают, что потоки импульса и углового момента j_A и j^l_AB, заданные выражениями (12.1.5.2) и (12.1.5.3),

в граничных точках струны равны нулю, так что все пуанкаре-заряды сохраняются, как и должно быть, если струна действи­тельно движется совершенно свободно.

Упражнения

1. Задачи на вариационный принцип без граничных ус­ловий:

а. Рассмотрите скалярное поле X в двумерном плоском про­странстве с обычным уравнением Клейна — Гордона. Напишите приведенное действие для конфигураций вида

Х(т, а) = а(т) cos2а + 6 (т) sin а,

Струна Намбу — Гото: классический анализ 115

Покажите, что условие экстремума приведенного действия по отношению к а и Ь не приводит к правильным дифференциаль­ным уравнениям.

б. Покажите, что трудность возникает вследствие неравных нулю поверхностных членов.

2. Жестко вращающаяся струна [10]:

а. Покажите, что траектория

= т, Х¹=^Л(а- ф) cos ют, Х² = А(о- л/2) sin ют, X³ = 0,

где А и со — постоянные, связанные соотношением ¹/2па>А = 1, является решением классических уравнений движения струны в четырех измерениях.

б. Покажите, что граничные условия также выполняются.

в. Исследуйте светоподобные кривые на мировом листе струны. Вычислите время Минковского, необходимое для того, чтобы световой сигнал с одного конца струны достиг другого конца. Заметим, что это время конечно (даже с учетом вырож­ дения метрики на границах), поэтому концы струны не яв­ ляются причинно несвязанными с внутренними точками струны.

г. Вычислите сохраняющиеся токи. Покажите, что масса и угловой момент определяются выражениями

М = Лэт/4а', / = А²/16а' и, следовательно,

/ = а'М²

(линейная траектория Редже).

д. Являются ли токи ;*, /5в ^везД^е времениподобными? Объ­ ясните.

е. Рассмотрите пересечения траектории струны с изотроп­ ными плоскостями Х° + X³ = const. Являются ли эти пересече­ ния времениподобными, светоподобными или пространственно- подобными?

За. Покажите, что решений уравнений движения и гранич­ных условий в двумерном пространстве Минковского не суще­ствует; метрика, индуцированная в граничных точках струны, не может быть вырожденной (необходимо еще одно простран­ственное направление, вдоль которого двигаются концы стру­ны под прямым углом к струне).

36. Рассмотрите геометрическое значение результата. Пока­жите, что для вариаций 6Х^А(%, а), не исчезающих на границе, не существует способа сделать площадь экстремальной (в двух измерениях).

Зв. Что произойдет, если потребовать, чтобы Х^А-}-6Х^А не было пространственноподобным в точках а = 0,зт? Покажите,

116 Глава 12

как можно построить (тривиальную) струнную теорию в двух: измерениях.

Зг. Заключение: струна в двумерном (фоновом) простран­стве является плохим примером того, что может быть при: