
- •О.И.Москвич общая физика Молекулярная физика
- •Предисловие
- •I. Основы молекулярной статистики
- •1.1. Предмет молекулярной физики
- •1.2. Масштабы физических величин в молекулярном мире
- •1.3. Теоретические и экспериментальные методы молекулярной физики
- •1.4. Эволюция молекулярных систем. Порядок и хаос
- •1.5. Принципы организации статистического и термодинамического методов изучения макросистем
- •Статистический метод
- •Термодинамический метод
- •2.1. Классификация моделей молекулярных систем
- •2.2. Идеальные статистические системы
- •Модели идеальных систем
- •2.3. Элементарные сведения из теории вероятностей
- •Случайные события
- •Определения вероятности событий
- •Статистическое или частотное определение вероятности.
- •Теоремы теории вероятностей
- •Условие нормировки вероятности
- •Случайная величина
- •Плотность вероятности
- •2.4. Основные понятия молекулярной статистики
- •Вероятность микроскопического состояния. Статистический ансамбль
- •Статистические постулаты
- •Комментарий к постулату равновероятности
- •Эргодическая гипотеза:
- •Постулат равновероятности доступных микроскопических состояний изолированной системы в состоянии термодинамического
- •Комментарий к эргодической гипотезе
- •Вероятность макроскопического состояния
- •3.1. Вывод закона распределения вероятностей Описание системы
- •Актуальные свойства модели системы
- •Постановка задачи
- •Вывод закона
- •Математические преобразования больших чисел. Введение общепринятых обозначений
- •Формула для вероятности макросостояния. Закон Бернулли, или биномиальное распределение.
- •3.2. Графическое представление биномиального распределения.
- •Основные характеристики биномиального распределении.
- •3.3. Предельные случаи биномиального распределения
- •4.1. Распределение энергии в статической системе
- •Вывод распределения Гиббса
- •4.2. Вывод распределения Максвелла
- •4.3. Плотность вероятности и характерные скорости распределения Максвелла
- •4.4. Распределение Максвелла по компонентам скорости
- •4.5. Экспериментальная проверка распределения Максвелла
- •5.1. Вывод формулы для давления идеального газа
- •5.2. Основное уравнение молекулярно-кинетической теории. Газовые законы
- •5.3. Уравнение эффузии
- •5.4. Измерение давления
- •5.5. Определение и измерение температуры
- •5.6. Построение эмпирической шкалы на основе газового термометра
- •Преимущества газовой шкалы температур
- •Построение газовой шкалы температур
- •Термодинамическая шкала температур
- •6.1. Распределение молекул по энергиям во внешнем потенциальном поле
- •6.2. Формула Больцмана для концентрации молекул в потенциальном поле
- •6.3. Зависимость концентрации молекул газа от координат в однородном гравитационном поле и поле центробежных сил
- •Графическое представление зависимости концентрации молекул от координат
- •6.4. Экспериментальное подтверждение распределения Больцмана: опыты Перрена
- •Получение макромолекул
- •Выделение частиц одинакового размера
- •Измерение диаметра макромолекулы
- •Подсчёт количества частиц на определённой высоте
- •6.5. Барометрическая формула
- •6.6. Закон распределения Максвелла – Больцмана
- •7.1. Формулировка теоремы и её доказательство Формулировка теоремы
- •Актуальные свойства модели статистической системы
- •Доказательство теоремы
- •7.2. Статистические степени свободы
- •7.3. Броуновское движение и его статистическое описание
- •Поступательное броуновское движение
- •Вращательное броуновское движение
- •7.4. Броуновский критерий точности физических измерений
- •7.5. Классическая теория теплоёмкости многоатомных газов. Область её применимости
- •7.6. Классическая теория теплоёмкости твёрдых тел.
- •7.7. Применение квантовых моделей в теории теплоёмкости твёрдых тел
- •Модель Эйнштейна
- •Модель Дебая
- •II. Основы термодинамики
- •8.1. Четыре постулата термодинамики
- •8.2. Нулевое (общее) начало термодинамики
- •Формулировка постулата
- •Свойство транзитивности термодинамического равновесия
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •8.3. Макроскопические процессы
- •8.4. Функция состояния
- •Математические свойства функции состояния
- •8.5. Внутренняя энергия системы. Работа и теплота Внутренняя энергия
- •Макроскопическая работа и теплота
- •8.6. Калорическое и термическое уравнения состояния
- •9.1. Первое начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •9.2. Теплоёмкость
- •Связь между теплоёмкостями и(общий случай)
- •Уравнение Роберта Майера
- •9.3. Политропические процессы в идеальном газе
- •Вывод уравнения политропического процесса в идеальном газе
- •9.4. Тепловые машины и их эффективность.
- •Принципиальная схема работы тепловой машины
- •Показатели эффективности тепловых машин
- •10.1. Цикл Карно
- •Расчёт кпд машины Карно
- •10.2. Теоремы Карно
- •Термодинамическая шкала температур
- •10.3. Метод циклов
- •Задача о нахождении зависимости внутренней энергии макроскопического тела от его объема
- •10.4. Неравенство Клаузиуса. Определение энтропии
- •10.5. Оценка эффективности тепловых машин сверху
- •Примеры оценок эффективности тепловых машин сверху кпд бензинового двигателя внутреннего сгорания
- •Кпд паровой турбины
- •Киэ бытового холодильника
- •Киэ кондиционера воздуха
- •Киэ теплового насоса
- •Тепловое загрязнение окружающей среды
- •11.1. Формулировки второго начала термодинамики
- •Энтропийная формулировка второго начала термодинамики Часть первая
- •Часть вторая
- •Информационное содержание постулата
- •11.2. Закон возрастания энтропии в изолированных системах
- •Демон Максвелла
- •Формулировка парадокса
- •Разрешение парадокса
- •11.3. Область применимости второго начала термодинамики
- •Статистический характер второго начала
- •11.4. Концепция тепловой смерти Вселенной
- •Концепция Клаузиуса
- •Флуктуационная гипотеза Больцмана
- •Несостоятельность концепции тепловой смерти Вселенной
- •11.5. Энтропия и её изменение в различных процессах
- •Постановка задачи
- •Описание системы
- •Актуальные свойства системы и процесса
- •Решение
- •Парадокс Гиббса Описание
- •По разные стороны перегородки находятся различные газы. После устранения перегородки начнется диффузия.
- •По разные стороны перегородки находится один и тот же газ.
- •12.1. Термодинамические функции
- •Свободная энергия
- •Термодинамический потенциал Гиббса
- •12.3. Условия термодинамической устойчивости макроскопических систем. Принцип Ле Шателье-Брауна
- •Принцип Ле Шателье-Брауна
- •Проведение полного термодинамического анализа вещества на полуэмпирической основе
- •12.4. Третье начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата (варианты)
- •Информационное содержание постулата
- •Статус постулата
- •Следствия третьего начала
- •III. Физика реальных макросистем
- •13.1. Твердые тела
- •13.2. Реальные газы и жидкости
- •Потенциал межмолекулярного взаимодействия
- •Природа межмолекулярного взаимодействия
- •Структура жидкостей
- •13.3. Переход из газообразного состояния в жидкое.
- •13.4. Уравнения состояния реального газа
- •13.5. Модель газа Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса
- •14.1. Изотермы газа Ван-дер-Ваальса
- •14.2. Критическое состояние вещества
- •Закон соответственных состояний
- •Свойства вещества в критическом состоянии
- •Анализ применения уравнения Ван-дер-Ваальса для описания свойств реальных газов
- •14.3. Внутренняя энергия газа Ван-дер-Ваальса
- •14.4. Эффект Джоуля-Томсона Основные определения
- •Описание процесса Джоуля-Томсона
- •Сущность эффекта Джоуля-Томсона
- •Расчет дифференциального эффекта Джоуля-Томсона
- •Расчет интегрального эффекта Джоуля-Томсона
- •14.5. Методы получения низких температур
- •Метод противоточного обмена теплотой
- •Метод адиабатического размагничивания
- •15.1. Условие равновесия фаз химически однородного вещества
- •15.2. Классификация фазовых переходов по Эренфесту
- •Фазовые переходы первого рода
- •Фазовые переходы второго рода
- •15.3. Фазовые переходы первого рода. Диаграмма состояний
- •15.4. Уравнение Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса методом циклов
- •Актуальные свойства процесса
- •Постановка задачи
- •Вывод уравнения
- •15.5. Диаграмма состояний гелия. Сверхтекучесть жидкого гелия.
- •16.1. Релаксационные процессы в молекулярных системах
- •16.2. Стационарные уравнения переноса в газах, жидкостях и твердых телах
- •Уравнение теплопроводности
- •Уравнение самодиффузии
- •Уравнение внутреннего трения
- •16.3. Внутренняя теплопроводность и внешняя теплопередача
- •Стационарное распределение температуры в бесконечной плоско-параллельной пластинке
- •Стационарное распределение температуры между двумя концентрическими бесконечно длинными цилиндрами
- •Стационарное распределение температуры между двумя концентрическими сферами
- •Внешняя теплопередача
- •17.1. Столкновения молекул и их количественные характеристики
- •Эффективное сечение молекул
- •Средняя длина свободного пробега молекулы
- •Кинематические параметры и
- •17.2. Обобщенное уравнение переноса
- •Вывод обобщенного уравнения процесса Описание системы
- •Актуальные свойства модели процесса
- •Постановка задачи
- •Вывод уравнения
- •17.3. Элементарная кинетическая теория теплопроводности,
- •17.4. Явления переноса в ультраразреженных газах
- •Трение и теплопроводность ультраразреженных газов
- •Тепловая и изотермическая эффузия
- •18.1. Атмосфера как открытая система и как открытая книга
- •18.2. Состав и структура атмосферы Земли.
- •18.3. Термофизическая модель атмосферы
- •18.4. Парниковый эффект
- •Сущность парникового эффекта
- •Парниковые газы
- •Проблема глобального потепления
- •Киотский протокол
- •18.5. Инверсия температуры в стратосфере. Озоносфера Земли
- •Мониторинг озонового слоя
- •Монреальский Протокол
- •18.6. Концепция «ядерной зимы»
- •«Ядерная зима» Сценарии ядерной войны
- •Огненные смерчи – суперподъемники
- •Антипарниковый эффект
- •Глобальный характер климатических последствий
- •Список литературы
- •Общая физика. Молекулярная физика
- •660041, Г. Красноярск, пр. Свободный, 79

Эргодическая гипотеза:
І. Начиная свое движение из любого возможного микроскопического состояния, статистическая система обязательно достигнет состояния, сколь угодно близкого к любому другому состоянию, совместимому с пространственными ограничениями и с законом сохранения энергии.
ІІ. Вероятность по ансамблю равна вероятности по времени:

Среднее по ансамблю равно среднему по времени:
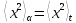
Постулат равновероятности доступных микроскопических состояний изолированной системы в состоянии термодинамического
равновесия:
І. Если изолированная статистическая система находится в состоянии термодинамического равновесия, то все доступные ей микроскопические состоянияравновероятны.
ІІ. Если микроскопические состояния изолированной статистической системыне равновероятны, то система не находится в состоянии термодинамического равновесия, но на пути к нему.
Комментарий к эргодической гипотезе
В первой части гипотезы постулируется (предполагается) свойство статистической системы, которое собственно и называется эргодичностью. Вторая часть формулировки является следствием первой части и решает вопрос об усреднении микроскопических параметров.
Микроскопические параметры, характеризующие
отдельные молекулы системы, постоянно
меняются во времени случайным образом.
Можно ли рассчитать средние значения
этих параметров с помощью применения
формальной процедуры? В качестве примера
рассмотрим усреднение квадрата координаты
определенной частицы,
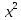 .
По определению среднего по времени
следует записать:
.
По определению среднего по времени
следует записать:
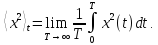
Изменение координаты будем рассматривать как результат перехода частицы из одной ячейки конфигурационного пространства в другую:
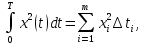
где
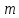 – число скачков в течении времени
– число скачков в течении времени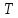 :
:

При
 частица много раз попадает в каждую
ячейку, за время
частица много раз попадает в каждую
ячейку, за время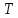 в -ой ячейке она проведет время
в -ой ячейке она проведет время
 ,
где сумма берется по всем
,
где сумма берется по всем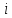 ,
соответствующимi-ой
ячейке;
,
соответствующимi-ой
ячейке;
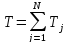 ;
с учетом вышеизложенного
;
с учетом вышеизложенного
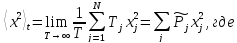
 – это выражение формально определяет
вероятность по времени. Однако рассчитать
эту вероятность невозможно, поскольку
невозможно хронометрировать «судьбу»
незримой частицы. Возникают вопросы:
– это выражение формально определяет
вероятность по времени. Однако рассчитать
эту вероятность невозможно, поскольку
невозможно хронометрировать «судьбу»
незримой частицы. Возникают вопросы:
• Равна ли вероятность по времени вероятности по ансамблю?
• Допустимо ли заменить «невозможную» процедуру усреднения по времени на процедуру усреднения по ансамблю?
Эргодическая гипотеза отвечает на эти вопросы утвердительно.
Впервые гипотеза была высказана в 1871г. Л.Больцманом, затем Дж.Максвелл в 1879г. проанализировал возможность замены средних по времени средними по ансамблю.
Вероятность макроскопического состояния
Если известны признаки интересующего
нас макроскопического состояния системы
(обозначим их
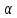 ),
то можно, в принципе, зафиксировать и
подсчитать все микросостояния
),
то можно, в принципе, зафиксировать и
подсчитать все микросостояния ,
совместимые с этими признаками. Пусть
,
совместимые с этими признаками. Пусть общее число микроскопических состояний,
доступных системе в соответствии с
эргодической гипотезой. Тогда, исходя
из постулата равновероятности
микросостояний, согласно (2.3) получим
формулу для вероятности макроскопического
состояния
общее число микроскопических состояний,
доступных системе в соответствии с
эргодической гипотезой. Тогда, исходя
из постулата равновероятности
микросостояний, согласно (2.3) получим
формулу для вероятности макроскопического
состояния
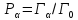 ,
,
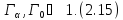
Число микроскопических состояний
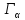 ,
приводящее к данному макроскопическому
состоянию, называется термодинамической
вероятностью макросостояния. Задачей
теории является нахождение
,
приводящее к данному макроскопическому
состоянию, называется термодинамической
вероятностью макросостояния. Задачей
теории является нахождение и
и ,
желательно не пересчитывая их. Лучшим
вариантом, конечно было бы нахождение
сразу вероятности
,
желательно не пересчитывая их. Лучшим
вариантом, конечно было бы нахождение
сразу вероятности ,
не зная
,
не зная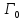 и
и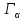 и это порой возможно. Для этого существуют
особые математические приемы. Некоторые
из них мы рассмотрим в последующем.
и это порой возможно. Для этого существуют
особые математические приемы. Некоторые
из них мы рассмотрим в последующем.
Контрольные вопросы
1. Какие молекулярные системы называются идеальными? Приведите примеры.
2. Опишите модель системы идеальных спинов. Чему равно количество проекций спина на выделенное направление?
3. Что называется случайным событием? Дайте определения различным видам случайных событий.
4. Как определяется вероятность случайного события? В чем различие классического и статистического определений вероятности?
5. Что называется случайной величиной? Назовите основные числовые характеристики случайной величины. Запишите формулы для их нахождения.
6. Что называется плотностью вероятности? Запишите для нее условие нормировки.
7. Сформулируйте две теоремы теории вероятностей рассмотренных на лекции. Какая из них лежит в основе условия нормировки вероятности? Дайте математическое обоснование.
8. Что называется микроскопическим состоянием системы? Какие параметры используются для его описания в классических и квантовых системах?
9. Что называется микроканоническим статистическим ансамблем?
10. Как определяется вероятность микроскопического состояния по ансамблю и по времени?
11. Сформулируйте статистические постулаты. Поясните их смысл.
12. Дайте определение вероятности макроскопического состояния статистической системы?
ЛЕКЦИЯ 3
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ПРЕДЕЛЬНЫЕ СЛУЧАИ В ОПИСАНИИ МОЛЕКУЛЯРНЫХ СИСТЕМ
При описании статистических систем нас, конечно же, интересует пространственное распределение частиц. Наличие каких-либо силовых полей или их отсутствие определяет различные законы распределения вероятностей. Начнем исследование с простейшего случая – равновесного пространственного распределения частиц классического идеального газа в отсутствии силовых полей. Наша задача получить закон распределения вероятностей на основе базового определения вероятности макроскопического состояния изолированной системы (2.15).
