7.1. Формулировка теоремы и её доказательство Формулировка теоремы

На каждую степень свободы статистической системы, находящейся в состоянии термодинамического равновесия, приходится одна и та же величина средней энергии:

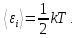
Актуальные свойства модели статистической системы

• Система находится в состоянии термодинамического равновесия.

• Распределение энергии между малыми частями системы (молекулами и атомами) описывается распределением Гиббса.

• Массы частиц могут быть различными.

• Температура системы соответствует области применимости классических идеальных моделей материального тела.

Доказательство теоремы

В основе доказательства лежит тот факт, что выражение для всех видов внутренней энергии молекулы, приходящейся на одну степень свободы, имеет однотипную квадратичную форму: 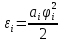, где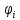– обобщённая координата, описывающая поступательное или вращательное движение молекулы как целого или колебательное движение отдельного атома в молекуле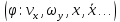. Положительная константаописывает инертные или упругие свойства микроструктуры.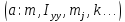

• Энергия молекулы

сумма всех квадратичных форм, исчерпывающе описывающая энергию сложной или простой частицы.

• Обратите внимание на то, что закон Гиббса применим к распределению энергии 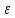, но не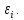Другими словами выражение

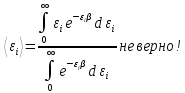
• Получить правильное и простое решение (доказательство) можно путём перехода от распределения по энергиям 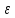к многомерному распределению по обобщённым координатам. Математическая структура этого распределения точно такая, как у распределения Максвелла в декартовой системе координат в пространстве скоростей.

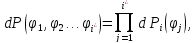
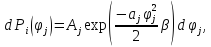
• Применим процедуру усреднения к квадрату обобщённой координаты:

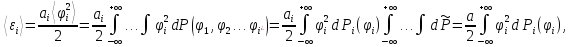
где 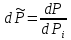,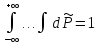– по условию нормировки.

• Оставшийся интеграл легко берётся по частям

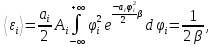
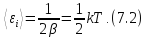
Что и требовалось доказать.

7.2. Статистические степени свободы

Опираясь на теорему равнораспределения энергии, можно сделать вывод, что для расчёта средней внутренней энергии любой молекулы идеального газа достаточно знать число квадратичных форм 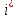в представлении её энергии в виде (7.1), тогда

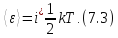
Число принято называть числом статистических степеней свободы молекулы.

Для вычисления 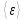не надо брать никаких интегралов, надо только суметь подсчитать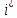. Это не сложно, поскольку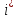зависит от механических степеней свободы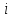. Различают поступательные, вращательные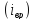и колебательные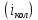степени свободы. Максимальное количество статистических степеней свободы многоатомной молекулы газа определяют следующим образом

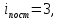
где 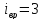(для нелинейной молекулы) или 2 (для линейной молекулы);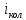определяют по остаточному принципу: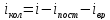. Полное число механических степеней свободы молекулывсегда равно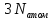(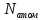– количество атомов в молекуле). Поясним на примере.

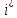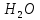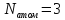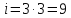Подсчитаем для молекул водяного пара. Молекуласостоит из трёх атомов (), значит. Учитывая, что структура молекулы нелинейная, запишем

Следовательно, средняя энергия молекулы водяного пара

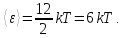
Теорема о равнораспределении используется при решении многих задач молекулярной физики, несмотря на достаточно ограниченную область температур, при которых она справедлива. Мы обсудим возможности применения теоремы при описании броуновского движения, а также при расчёте теплоёмкостей многоатомных газов и идеальных твёрдых тел.