Приложения

Приложение А (основное)

Введение в метод конечных элементов53

Современные информационные технологии позволяют существенно повысить производительность труда в управлении производством, проектировании и исследовании объектов и процессов. В настоящее время ряд задач, считавшихся сугубо интеллектуальными и подлежащими компетенции только человека, перешли в разряд вычислительных, и ЭВМ во все большей степени вместо выполнения элементарных функций помощника-вычислителя начинает играть роль соавтора-конструктора. Теперь машине нужно задать уже не мелочно регламентированную последовательность предписанных вычислений, а только основные сведения об объекте исследования и постановку задачи. Даже выбор конкретного метода решения ЭВМ в принципе может сделать сама, опираясь, например, на сравнение объёмов вычислений по имеющимся в её распоряжении алгоритмам.

В последние десятилетия резко возросла сложность задач, которые ставит перед механикой техника. Как правило, эти задачи имеют объем, делающий невозможным их решение средствами традиционной «бумажно-ручной» технологии. Даже в тех случаях, когда соответствующие расчеты могут быть проведены вручную, они оказываются чрезвычайно громоздкими и занимают неоправданно много времени.

При неавтоматизированном проектировании результаты во многом определяются инженерной подготовкой кон-

53 Жилкин В. А. Расчеты на прочность и жесткость элементов сельскохозяйственных машин. Челябинск : ЧГАУ, 2005. 427 с.; Жилкин В. А. Элементы прикладной и строительной механики сельхозмашин. Применение программ MathCAD, SCAD, MSC/Patran-Nastran 2005. Челябинск : ЧГАУ, 2007. 349 с.; Никонов В. Н. Лекция третья. Введение в МКЭ. 2005–2008, ЦНЭАТ, г. Самара (www.cneat.ru); Жилкин В. А. Исследование плоского напряженного состояния пластин в программных продуктах SCAD, MSC.Patran- Nastran-2005 : метод. указ. Челябинск : ЧГАУ, 2007. 67 с.; Жилкин В. А. Определение геометрических характеристик поперечных сечений брусьев в программных продуктах SCAD, MSC.Patran-Nastran-2005, MathCAD : метод. указ. Челябинск : ЧГАУ, 2007. 66 с.; Жилкин В. А. Расчет на прочность и жесткость статически определимых балок в программных продуктах SCAD, MSC.Patran-Nastran-2005, MathCAD : метод. указ. Челябинск : ЧГАУ, 2007. 75 с.; Жилкин В. А., Шароухов В. В. Геометрическое моделирование в среде MSC.Patran-Nastran // Вестник ЧГАА. 2010. Т. 56. С. 160–250.

502

структоров, их производственным опытом, профессиональной интуицией и другими факторами. Автоматизированное проектирование позволяет значительно сократить субъективизм при принятии решений, повысить точность расчетов, выбрать наилучшие варианты для реализации на основе строгого математического анализа всех или большинства вариантов проекта с оценкой технических, технологических

иэкономических характеристик производства и эксплуатации проектируемого объекта, значительно повысить качество конструкторской документации, существенно сократить сроки проектирования и передачи конструкторской документации в производство, эффективнее использовать технологическое оборудование с программным управлением. Автоматизация проектирования способствует более полному использованию унифицированных изделий в качестве стандартных компонентов проектируемого объекта.

Внастоящее время в конструкторской практике используются специализированные интегрированные системы автоматизированного проектирования, в которых предусматривается полная автоматизация всех расчетных

ичертежных работ, а также технологической подготовки производства (проектирования технологической оснастки, опре-

деления оптимальных маршрутов, выбора оборудования и инструмента и др.). Кроме того, в них предусматривается полная или частичная автоматизация изготовления всей необходимой документации (чертежей, таблиц, текстов и др.). Для этой цели чаще всего используют программные продукты АПМ WinMachine, SCAD, СОSMOS, NASTRAN, ANSYS, ALGOR, COSМОS/Works 6.0 и др.

Анализ конструкций с использованием метода конечных элементов (МКЭ) является в настоящее время фактически мировым стандартом для прочностных и других видов расчетов конструкции. Основой этого служит универсальность МКЭ, позволяющая единым способом рассчитывать различные конструкции с разными свойствами материалов. Многовариантность способов моделирования конструкции

503

МКЭ влечет за собой большую вероятность появления скрытых ошибок, то есть ситуаций, когда результат анализа либо недостижим, либо абсурден, либо, что самое опасное и распространенное, правдоподобен, но не верен. Поэтому применение МКЭ требует от расчетчика более профессиональной подготовки. Чтобы с большой вероятностью получить достоверный результат, от пользователя пакета конечноэлементного анализа требуется знание принципов и методов реализации этого метода, глубокое понимание механики поведения конструкций в используемой области анализа и, наконец, владение методами выявления формальных и фактических ошибок.

МКЭ основан на мысленном представлении сплошного тела (континуума) в виде совокупности отдельных конечных элементов, взаимодействующих между собой в конечном числе узловых точек. В этих точках к каждому конечному элементу прикладываются некоторые фиктивные усилия взаимодействия, характеризующие действие распределенных внутренних напряжений, приложенных вдоль реальных границ стыковки смежных элементов. Если такая идеализация тела (конструкции) возможна, то проблема сводится к расчету системы с конечным числом степеней свободы.

Замена исходной конструкции совокупностью дискретных элементов подразумевает равенство энергий конструкции и ее дискретной модели. Для некоторых конструкций соблюдение энергетического баланса ведет к получению дискретной модели, точно описывающей поведение исходной конструкции. Это характерно для конструкций, которые уже состоят из отдельных элементов с дискретным сочленением их между собою. В качестве примера можно указать на фермы, рамы, стержневые перекрытия.

В стержневых системах конечным элементом является стержень, в котором напряжения и деформации определяются без особых затруднений по формулам сопротивления материалов. Чаще всего этот метод применяют в форме метода перемещений.

504

Плоская пластина произвольного очертания с помощью сечений, параллельных осям x и y, может быть представлена в виде совокупности прямоугольных и треугольных конечных элементов. Именно эти две формы конечных элементов нашли широкое использование при решении плоской задачи теории упругости.

При определении напряженного состояния трехмерных тел идеализация осуществляется уже с помощью объемных конечных элементов – параллелепипедов, тетраэдров и т. п., шарнирно скрепленных в узловых точках. При такой идеализации к каждой вершине конечного элемента прикладываются по координатным осям три составляющие усилий взаимодействия со смежными элементами.

Если же элементы реальной конструкции имеют вдоль своей границы непрерывные связи со смежными элементами, то при построении дискретной модели мы вынуждены делать некоторые априорные предположения о характере силового или кинематического взаимодействия между смежными элементами. В этом случае дискретная модель будет лишь приближенно отражать поведение исходной конструкции.

Очень важно выбрать характер взаимодействия между элементами таковым, чтобы уменьшение размеров конечных элементов привело к получению решения, стремящегося к точному.

Разбиение области на конечные элементы является первой операцией метода конечных элементов. Эта операция весьма ответственна. Здесь многое зависит от имеющихся инженерных навыков. Несовершенное разбиение будет приводить к значительным погрешностям расчета, если даже все остальные операции метода выполнены с достаточной точностью.

Использование более мелких конечных элементов, как правило, повышает точность решения, но приводит к увеличению общей трудоемкости расчета. В области изделия, где ожидается резкое изменение напряжений, деформаций, следует использовать более мелкую разбивку на элементы.

505

Там же, где ожидаемый результат изменяется по области сравнительно слабо, можно использовать при дискретизации более крупные элементы.

Пусть требуется выполнить расчет прямого консольного бруса, жестко защемлённого на одном торце и загруженного сосредоточенной силой на другом (рис. П.1). Представим заданный брус в виде двух линейных конечных элементов, первый из которых имеет узлы 1 и 2, а второй – узлы 2 и 3, т. е. узел 2 является общим для соседних конечных элементов.

Рис. П.1

Рис. П.2

Прежде чем решать конкретную задачу, уясним свойства линейного конечного элемента.

Рассмотрим абстрактный линейный конечный элемент длиной L с узлами i, j и жесткостью поперечного сечения EJy (рис. П.2). Свяжем с элементом прямоугольную декартовую правую локальную систему координат xOz: ось x направим от узла i к узлу j. Выразим перемещения любой точки конечного элемента через линейные wi , w j и угловые 1 , 2 перемещения его узлов.

При прямом поперечном изгибе бруса каждое его сечение имеет две степени свободы: сечение бруса может поступательно перемещаться в направлении оси z на величину w и может поворачиваться относительно нейтральной оси y на угол . Поэтому при прямом поперечном изгибе каждая точка элемента с узлами i и j имеет те же две степени свободы. Так как конечный элемент представлен двумя узлами, то он имеет четыре степени свободы. В самом простом варианте прогиб любой точки x элемента, представляющего часть упругой

506

линии бруса, можно описать полиномом третьего порядка с четырьмя коэффициентами:

w a	a x a		x2 a x3 .	(П.1)
1	2	3	4

Прогиб и угол поворота поперечного сечения бруса связаны зависимостью

dw
dx ,
откуда с учетом зависимости (П.1)
a2 2a3 x 3a4 x2 .	(П.2)

Воспользовавшись граничными условиями: при x 0

w wi , i ; при x L w w j , j , – и выражениями (П.1), (П.2), получим систему четырёх алгебраических урав-

нений для определения коэффициентов функции перемещений w x :

wi a1 ;

1 a2 ;

w j a1 a2L a3L2 a4L3 ;

j a2 2a3L 3a4L2 ,

решая которую

,

507

получим выражение прогибов участка бруса в любой его точке через перемещения узлов – основных неизвестных задачи:

								2			3									x	2	3
w x				1	3			x	2	x			wi			x			2				x		i
								2		3										L			2
								L		L													L
	2				3							x		2		3
	3	x	2			x		w j									x		j .						(П.3)
		2				3											2
		L				L							L				L

Теперь, зная длину элемента L, перемещения в узлах конечного элемента wi , w j , 1 , 2 и координату какой-либо точки x, можно определить прогиб и угол поворота поперечного сечения бруса.

Громоздкую запись последней формулы можно устранить, записав ее в матричном виде. Введем вектор узловых перемещений конечного элемента e в виде

wi

i

e

w j

.

(П.4)

j

Введём вектор формы элемента N

1

3

x2

2

x3

2

3

L

L

x 2

x2

x3

L

2

(П.5)

N

L

.

3

x

2

2

x3

L2

L3

x2

x3

L

2

L

Теперь выражение (П.3) можно записать в матричной форме:

w N
T		e		,	(П.6)

где верхний индекс T – операция транспонирования матрицы.

508

По (10.6) и (10.34)

z

z d2w

dx2

или

d2 N T

e

z

z B

e

,

(П.7)

dx2

где

6

6x

L3

L2

4

6x

2

w2 B e

; B

2

d

L

L

,

(П.8)

dx

6

6x

L2

L3

2

6x

L

L2

компоненты вектора B

получены путём вычисления вто-

рых производных от компонент вектора N .

Согласно закону Гука,

E Ez B

(П.9)

e .

Из (10.9) следует зависимость

My

x Jy

,

z

позволяющая записать вектор узловых нагрузок:

F EJy B e .

(П.10)

Итак, зависимости (П.7), (П.9), (П.10) позволяют определить вектора относительных деформаций, напряжений

и узловых нагрузок по известному вектору узловых перемещений e .

509

Истинные перемещения любой деформированной конструкции обеспечивают минимум полной энергии деформаций.

Перепишем зависимость для удельной потенциальной энергии (5.29) в матричной форме:

	1					1	1		T	1
u		1 1	2 2	3 3				2			2
	2					2
								3			3
	1	T ,
	2

1

где 2 – вектор напряжений;

3

1

2 – вектор относительных деформаций.

3

Энергия, накопленная в балочном элементе, определяется зависимостью (5.39):

1

1

L

M

y

T

1

M

y

U

udV

T dV

z

z dF dx

2

2

J

E

J

y

y

V

V

0 F

1 L MT

1

M

dx 1

L d2w T

EJ

d2w dx

2

2 0

Y

EJy

y

2

y

2

0 dx

dx

1 L B e T EJy B e dx

2 0

1 e T L B T EJy B dx e .

2 0

Выражение

ke L B T EJy B dx

0

510

Рис. П.3

Рис. П.4

называется матрицей жесткости конечного элемента (КЭ). Следовательно, энергия, накопленная в балочном элементе, определяется по формуле

U

1

T

k

e

e

e

.

(П.11)

2

k

Матрицу жесткости

e элемента

ij

можно вычислить непосредственно.

Элементы матрицы жесткости КЭ пред-

ставляют собой реакции в узлах от еди-

ничных

перемещений. В

поперечных

сечениях бруса при прямом поперечном

изгибе возникают только два внутрен-

них силовых фактора: поперечная сила

Qz

и изгибающий момент My . На рас-

четных схемах рис. П.3 и рис. П.4 единичные перемещения будем изображать положительными.

Для консольного бруса, жестко заделанного на правом торце и нагруженного на свободном левом торце парой сил, максимальные линейные w и угловые перемещения определяются зависимостями (10.36) и (10.37):

wmax ML2 ; max ML ,

2EJy EJy

а для консольного бруса, загруженного сосредоточенной силой, – зависимостями (10.38) и (10.39):

wmax	QL3	; max	QL2	.
	3EJy
			2EJy

Задаём в узле i единичное перемещение wi 1 , а все остальные перемещения в узлах i и j равны нулю:

wi 1 wi Q wi M QiL3 MiL2 ;

3EJy 2EJy

511

i 0 i Q i M QiL2 MiL2 .

2EJy 2EJy

Из полученной системы уравнений определяем внутренние силовые факторы Qi и Mi :

Qi

12EJy

;

(а)

L3

Mi

6EJ

y

.

(б)

2

L

Реакции в заделке (в узле j):

Qj

12EJ

y

;

(в)

3

L

12EJy

6EJy

6EJy

M

Q L M

.

(г)

L2

L2

j

i

i

L2

Запишем уравнения (а)-(г) в матричной форме:

			12EJy
					3
Qi						L
					6EJy
Mi					2
						L
Qj					12EJy
						3
Mj						L
					6EJ		y
						L2

0	0	0
				1
0	0	0
				0		(П.12)
					.
0	0	0		0
				0
0	0	0

Используя подобную процедуру и устанавливая значения перемещений wi 0 ; i 1 ; w j 0 ; j 0 , получим

512

;

6EJ

Qi

y

;

(д)

L2

Mi

4EJy

.

(е)

L

Реакции в заделке (в узле j):

Qj

6EJ

y

;

(ж)

3

L

Mj QiL Mi

6EJy

4EJy

2EJy

.

(3)

L

L

L

Уравнения (д)-(з) в матричной форме имеют вид

				0		6EJy
							2
	Qi						L
						4EJy
				0
							L
	Mi
							6EJy
	Qj			0
							2
	Mj						L
						2EJy
				0
							L

0	0
			0
0	0
			1		(П.13)
				.
0	0		0
			0
0	0

Аналогично, полагая wi 0 ; i 0 ; w j 1 ; j 0 и wi 0 ; i 0 ; w j 0 ; j 1 и объединяя все матричные уравнения типа (П.12), (П.13), мы получим

513

			12EJy
					3
Qi						L
					6EJy
Mi					2
						L
Qj					12EJy
						3
Mj						L
					6EJ		y
						L2

6EJ

y

12EJ

y

6EJ

y

2

3

2

L

L

L

1

4EJy

6EJy

2EJy

L

2

L

1

L

.

(П.14)

6EJy

12EJy

6EJy

1

2

3

2

L

L

L

1

2EJ

y

6EJ

y

4EJ

y

L

L2

L

Первый сомножитель в правой части зависимости (П.14) является матрицей жесткости балочного элемента

12EJ

y

6EJ

y

12EJ

y

6EJ

y

3

2

3

2

L

L

L

L

6EJy

4EJy

6EJy

2EJy

e

L2

L

L2

L

(П.15)

k

12EJy

6EJy

12EJy

,

6EJy

L3

L2

L3

L2

6EJ

y

2EJ

y

6EJ

y

4EJ

y

L2

L

L2

L

второй вектор – вектор единичных перемещений. Для других перемещений это уравнение является уравнением прямого поперечного изгиба элемента ij:

			12EJy
					3
Qi						L
					6EJy
Mi					2
						L
Qj					12EJy
						3
Mj						L
					6EJ		y
						L2

6EJ

12EJ

y

y

2

3

L

L

4EJy

6EJy

L

2

L

6EJy

12EJy

2

3

L

L

2EJy

6EJy

L

2

L

	6EJy
		2
		L					wi
	2EJy
		L					i
								. (П.16)
		6EJy					w j
		L2
	4EJ		y					j
		L

514

С помощью уравнения (П.16) можно решать задачи, в которых в одном направлении связаны несколько элементов.

Обобщённая матрица жесткости всей системы определяется в результате последовательного объединения матриц жесткости отдельных элементов. Этот этап расчета МКЭ является весьма ответственным и очень громоздким. Поэтому при практических расчетах формирование матрицы жесткости системы реализуется на ЭВМ. Мы же эту операцию для понимания процедуры конечно-элементного расчета проделаем «вручную».

Для дальнейших операций матрицу жесткости балочного конечного элемента удобно представить в виде

			k	k	k	k
			11	12	13	14
	e		k21	k22	k23	k24
k			k31	k32	k33	k34	.
				k42	k43	k44
			k41

Внутренним силовым факторам будем приписывать два индекса mn, первый из которых будет соответствовать элементу, второй – узлу.

Итак, консольную балку мы аппроксимируем двумя конечными элементами, для каждого из которых можно записать уравнение (П.16):

Q				k		k		k
	11				11		12		13
M11				k21		k22		k23
				k31		k32		k33
Q12
M				k	41	k	42	k	43
	12
Q				k		k		k
	22				11		12		13
M22				k21		k22		k23
				k31		k32		k33
Q23
						k42		k43
M23				k41

k	w
14	1
k24	1
k34			;
	w2
k44
	2
k	w
14		2
k24	2
k34			.
	w3
k44
	3

515

Определим систему сил, действующих на каждый узел, путём суммирования соответствующих усилий, действующих на элементы, сходящиеся в рассматриваемом узле.

Узел 1. В этот узел приходит только первый элемент, и поэтому

Q1 Q11 k11w1 k12 1 k13w2 k14 2 ;	(и)
M1 M11 k21w1 k22 1 k23w2 k24 2 .	(к)
Узел 2. В этом узле сходятся оба элемента, и поэтому
Q2 Q12 Q22 k31w1 k32 1 k33w2 k34 2
k11w2 k12 2 k13w3 k14 4 k31w1 k32 1
k11 k33 w2 k12 k34 2 k13w3 k14 4 ;	(л)
M2 M12 M22 k41w1 k42 1 k43w2 k44 2
k21w2 k22 2 k23w3 k24 3 k41w1 k42 1
k21 k43 w2 k22 k44 2 k23w3 k24 3 .	(м)
Узел 3. В этот узел приходит только второй элемент, и поэтому
Q3 Q23 k31w2 k32 2 k33w3 k34 3 ;	(н)
M3 M23 k41w2 k42 2 k43w3 k44 3 .	(о)

Переписывая уравнения (и)-(о) в матричной форме, получим матричное уравнение метода конечных элементов для принятой нами модели консольной балки:

Q1		k11			k12	k13		k14		0
M1		k21			k22	k23		k24		0
Q2		k31			k32	k33	k11	k34	k12	k13
					k42	k43	k21	k44	k22	k23
M2		k41
Q3			0	0		k31		k32		k33
						k41		k42		k42
M3			0	0

0	w1
0
	1
k14	w2
k24		. (П.17)
	2
k34
	w3
k44	3

516

Ведём обозначения

Q1

k11

k12

k13

k14

0 0

w1

M

k

21

k

22

k

23

k

24

0 0

1

1

Q2

k31

k32

k33 k11

k34 k12

k13

k14

w2

F

; K

k42

k43 k21

k44 k22

k23

; u

,

M2

k41

k24

2

Q

0 0

k

31

k

32

k

33

k

34

w

3

3

M3

0 0

k41

k42

k42

k44

3

придав тем самым уравнению (П.17) форму основного ма-

тричного уравнения метода конечных элементов:

	,
F K u		(П.18)

где F – вектор обобщённых сил (вектор объёмных и поверхностных сил, приложенных к вершинам элементов);

K – матрица жесткости конечно-элементного аналога конструкции;

u – вектор обобщённых перемещений.

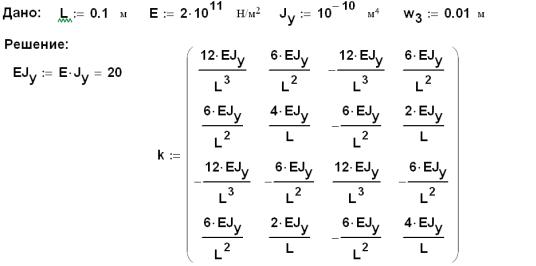
Зададим материал консольной балки и её геометрические характеристики: E 2 1011 Па, длины элементов – L = 0,1 м, осевой момент инерции – Jy 10 10 м4.

Пусть сила P вызвала перемещение вниз правого торца балки на 0,01 м, т. е. w3 0,01 .

ВычислимматрицужесткостиконсольнойбалкивMathCAD.

517

Обобщённые (узловые) силы пока не заданы, и компоненты глобального вектора узловых сил равны нулю:

00

F 0

0 .00

Зададим граничные условия. В узле № 1 имеет место жесткое защемление бруса, т. е. перемещение и угол поворота сечения в узле равны нулю, или w1 0 и 1 0 . Поэтому обнуляем первую и вторую строки и первый и второй столбцы матрицы жесткости, ставим на главные диагонали по 1. Получаем

518

Теперь из решения системы уравнений всегда будет

w1 0 и 1	0 .
Зададим перемещение узла № 3 вниз на 10 мм, или
w3 0,01	м. Для этого сформируем некоторый вектор R
в виде
			0
			0
	R		0
			0
		0.01
			0

и получим измененный вектор F по алгоритму

F F K R ,

т. е. вычтем из вектора F произведение K R – усилия, возникающие в узлах КЭ модели балки, при смещении узла 3 вниз на 10 мм, а результат поместим снова в вектор F . Теперь вектор F выглядит как

.

519

Обнулим пятую строку и пятый столбец матрицы K , поставим в главной диагонали на пятой строке 1, поставим в векторе F на пятой строке –0,01. Граничное условие внесено, а матрица и вектор F имеют вид

Решаем систему уравнений (П.18). В результате получаем

,

т. е. w1 0 , 1	0 , w2 3,125 мм, 2 0,056 рад,
w3 10 мм, 3	0,075 рад. Теперь, когда узловые пере-

мещения найдены, можно подставить их в формулу (П.6) для перемещения w и построить упругую линию бруса.

Прежде чем это сделать, найдём силу P, вызвавшую перемещение конца консоли вниз на 10 мм:

P	w3EJ	y	.
	3
	L
В соответствии с теоретическим решением упругая ли-
ния описывается уравнением
EJyw x				P x L 3	PL2 x	PL3 .	(Ф)
		6			2	6

520

Сопоставим результаты расчета по методу КЭ (формула П.6) и по формуле (Ф).

521

Приложение Б (дополнительное)

Ключи к вопросам ЕГЭ

Глава 1

Основные понятия, определения, допущения принципы

I	II	III	IV	V
3	3	3	2	1

Модели прочностной надежности

III

34

Внутренние силы и напряжения

I	II	III
2	4	4

Нормальнаяипоперечнаясилы, изгибающиймоментиихэпюры

I	II	III		IV	V	VI
3	1	4		4	1	1
		Глава 3
Виды напряженного состояния
I	II	III
2	2	1

Напряженное состояние в точке. Главные площадки и главные напряжения

I	II	III
3	2	3
		Глава 4
Перемещения и деформации
I	II	III
4	3	4
		Глава 5
Связь между напряжениями и деформациями
I	II	III		IV		V
3	2	2		3		2
		Глава 6

Испытание конструкционных материалов на растяжение и сжатие

I	II	III	IV
2	4	2	3

522

Механические свойства материалов

I	II	III		IV
1	1	1		2
		Глава 8
Напряжения и деформации
I	II	III		IV
4	3	1		4
Расчеты стержней на прочность и жесткость
I	II	III		IV		V
4	3	4		2		2
		Глава 9
Чистый сдвиг. Расчет на сдвиг (срез)
I	II	III
1	3	1
Крутящий момент. Деформации и напряжения
I	II	III		IV
1	1	4		2
Расчет на прочность при кручении
I	II	III		IV		V
3	2	2		3		2
Расчет на жесткость при кручении
I	II	III		IV		V
2	1	4		2		1
		Глава 10
Напряжения в поперечном сечении балки
I	II	III		IV		V
1	4	2		4		4
Расчет балок на прочность
I	II	III		IV		V
3	3	1		3		2

Перемещения при изгибе. Расчет балок на жесткость

I	II	III	IV	V
2	3	4	2	4

523

Учебное издание

Жилкин Виталий Афанасьевич

Сопротивление материалов

Учебное пособие

Редактор

С. А. Медведева

Технический

редактор

М. В. Шингареева

Редакционно-издательский отдел Челябинской государственной агроинженерной академии 454080, г. Челябинск, пр. Ленина, 75

Формат 60×84/16. Объем 25,0 уч.-изд. л. Тираж 300 экз. Заказ №

УОП ЧГАА