Глава 14 - Динамика и прочность ГТД

ГЛАВА 14 - ДИНАМИКА И ПРОЧНОСТЬ ГТД

Создание ГТД высокой надежности и ресурса работы требует тщательного исследования вопросов прочности. В настоящем разделе рассмотрены основные проблемы, которые приходится решать для обеспечения статической и динамической прочности деталей и узлов. Приведены необходимые для понимания материала теоретические основы методов прочностного анализа. Рассмотрены условия нагружения, расчетные схемы, методы расчета, закономерности напряженного состояния и колебаний типичных деталей и узлов ГТД. Особое внимание уделено современным методам прочностного и динамического анализа, их месту в системе исследований прочности ГТД.

14.1 - Теоретические основы динамики и прочности ГТД

Обеспечение прочностной надежности, под которой понимается предотвращение поломок или недопустимой деформации элементов конструкции, является одной из основных задач проектирования, производства и эксплуатационного обслуживания двигателей. Основной количественной характеристикой надежности является вероятность безотказной работы в течение заданного ресурса. Поскольку на стадии проектирования двигателя непосредственное определение этой характеристики затруднительно, для оценки прочностной надежности пользуются коэффициентами запаса проч- ности. Кроме того, поскольку часто разрушение деталей представляет собой процесс постепенно-

Рисунок 14.1_1 - Схема моделирования прочностной надежности

920

Глава 14 - Динамика и прочность ГТД

го накопления повреждений, пользуются оценкой долговечности.

Методология обеспечения прочностной надежности (см. Рис. 14.1_1) состоит в расчетном

èэкспериментальном моделировании нагружения деталей и их поведения в условиях эксплуатации. Термин «моделирование» здесь отражает понимание отличия реальных процессов, происходящих при эксплуатации детали в двигателе, и тех представлений об этих процессах, которые удается реализовать в расчетах и экспериментах. Для определения критериев прочностной надежности (коэффициентов запаса, долговечности, вероятности поломки) необходимо обоснованно выбрать или разработать модельные (упрощенные) представления о поведении материала, форме детали, действующих нагрузках и механизме разрушения.

Выбор этих моделей – неформализуемая задача отыскания компромисса между сложностью

èтрудоемкостью анализа с одной стороны, и точ- ностью достоверностью результатов – с другой.

Результатом прочностного анализа является обоснованный выбор формы, размеров, материала детали (на стадии проектирования), технологических параметров, режимов термообработки и т.д. (на стадии производства), методов и периодичности контроля (на стадии эксплуатации).

Используемые в практике конструирования ГТД методы прочностного и динамического анализа опираются на современные подходы, развиваемые в механике деформируемого твердого тела. В настоящем разделе приведены сведения, которые выходят за рамки обычного инженерного образования в области прочности (курсов сопротивления материалов, деталей машин), но необходимы для понимания изложенного с следующих разделах. Рассмотрены базовые положения основных разделов механики деформируемого твердого тела: теорий упругости, пластичности, ползучести, колебаний. Приведены необходимые сведения о моделях разрушения применяемых в ГТД.

Методы механики деформируемого твердого тела позволяют решать задачи прочности ГТД в более точной постановке, с меньшим числом допущений, чем более простые методы сопротивления материалов. Они могут использоваться как для проверки и уточнения упрощенных методов, так

èдля исследования наиболее сложных деталей

èусловий нагружения.

Далее мы будем опираться на обычные в механике деформируемого твердого тела допущения о сплошности и однородности материала; будем считать, если иное не оговорено, что материал изотропен, а деформации малы.

14.1.1 - Напряженное состояние, тензор напряжений

Напряженное состояние в некоторой точке деформируемого твердого тела характеризуется напряжениями на трех взаимно перпендикулярных площадках, проходящих через эту точку. На Рис. 14.1.1_1 показан элементарный параллелепипед, внутри которого расположена рассматриваемая точка, его грани - площадки, перпендикулярные осям координат x, y, z. Напряжения на этих площадках можно разложить на три составляющие, напряженное состояние в точке определено, если будут известны девять компонент напряжений. Эти составляющие можно записать в виде тензора напряжений:

или в индексной форме

(14.1.1-1)

В каждой строчке записаны три составляющих напряжения, действующих по одной площадке, первый индекс – наименование (в индексной форме – номер) оси, перпендикулярной к этой площадке. Второй индекс - наименование оси, параллельно которой действует напряжение. Напряже-

íèÿ σx, σy, σz или в индексной форме σ11, σ22, σ33 – нормальные (направленные по нормали к соответ-

ствующей площадке), остальные - касательные. Если, например, площадка параллельна плоскости ó0z (см. Рис. 14.1.1_1), то нормалью к этой площадке будет ось õ, и составляющие напряжения будут иметь обозначения σx, τxy è τxz или в индексной фор-

ìå σ11, σ12, σ13 .

Нормальное напряжение положительно, если оно растягивающее, и отрицательно - если сжимающее. Правило знаков для касательных напряжений понятно из Рис. 14.1.1_1, где показанные компоненты напряжений положительны.

При повороте элементарного параллелепипеда вокруг осей координат компоненты напряжений меняются. Как известно из сопротивления материа-

921

Глава 14 - Динамика и прочность ГТД

Рисунок 14.1.1_1 - Обозначение компонентов тензора напряжений

лов, возможно такое положение площадок, когда касательные напряжения исчезают, а нормальные приобретают наибольшие значения. Такие напряжения – главными напряжениями и обозначают в порядке убывания σ1, σ2 è σ3, а площадки, на которых они действуют - главными площадками. Главные напряжения не зависят от расположения исходных осей x, y, z, т.е. они инвариантны по отношению к выбору системы координат. В теории упругости получены соотношения для определения главных напряжений через компоненты тензора напряжений (см., например, [14.8.1]).

При анализе прочности конструкций для характеристики напряженного состояния в точке применяется инвариантная относительно выбора системы координат величина – интенсивность напряжений

(14.1.1-2)

стоящей на расстояние dx (èëè dy èëè dz) напряжения получают приращения. Например на грани, перпендикулярной оси x, в связи с приращением координаты на dx напряжения σx, τxy è τxz, являющиеся непрерывными функциями x, изменяются и становятся:

σx + äσx/äõ·dx, τxy + äτxy /äõ·dx, τxz +äτxz /äõ·dx

Можно определить напряжения на всех гранях элементарного параллелепипеда, как показано на Рис. 14.1.2_1. Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, Y è Z.

Если приравнять нулю сумму проекций на ось õ всех нормальных, касательных и объемной сил, действующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение:

äσx /äx + äτyx /äy + äτzx /äz + X = 0 (14.1.2-1)

Составив аналогичные уравнения проекций сил на оси ó è z, напишем три дифференциальных уравнения равновесия элементарного параллелепипеда:

14.1.2 - Уравнения равновесия

Выделим у исследуемой точки с координатами õ, ó è z элементарный параллелепипед с размерами dx, dy è dz (см. Рис. 14.1.2_1). По каждой из трех взаимно перпендикулярных граней, примыкающих к точке (ближайших к плоскостям координат), действуют три составляющих напряжения -

нормальное и два касательных. Считаем, что по Рисунок 14.1.2_1 - К выводу уравнений равновесия

граням, примыкающим к рассматриваемой точке, они положительны. При переходе от грани, проходящей через точку, к параллельной грани, от-

922

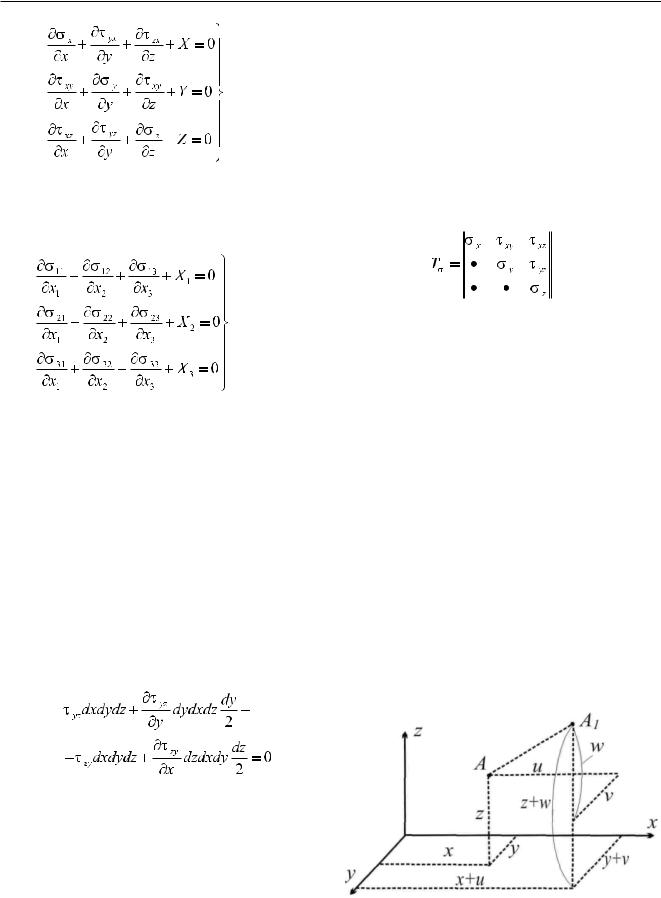
Глава 14 - Динамика и прочность ГТД

(14.1.2-2)

Используя индексные обозначения осей и компонент тензора напряжений можно записать эту систему уравнений как:

или в свернутой тензорной форме:

σijj + X = 0,

(14.1.2-3)

ãäå i, j = 1, 2, 3.

В этой записи используются следующие правила. По повторяющемуся «немому» индексу i проводится суммирование от 1 до 3; запятая обознача- ет дифференцирование по указанной после запятой координате с индексом j.

Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси, параллельной оси õ и проходящей через его центр тяжести, получим уравнение:

Отсюда, пренебрегая слагаемыми высшего порядка малости по сравнению с остальными, после сокращения на dxdydz, получаем τyz = τzy. Составив аналогичные уравнения моментов относительно центральных осей óc è zc, получим три уравнения закона парности касательных напряжений: касательные напряжения, действующие по взаимно перпендикулярным площадкам равны по величи- не и одинаковы по знаку:

τxy = τyx, τyz = τzy, τzx = τzx

(14.1.2-4)

или в тензорной форме

σij = σji ïðè i ≠ j

Таким образом, из девяти составляющих напряжений матрицы тензора Òσ шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следующие шесть компонент:

Условия равновесия дают лишь три уравнения (14.1.2-2), следовательно задача определения напряженного состояния в точке в общем случае стати- чески неопределима. Для раскрытия статической неопределимости необходим анализ деформаций.

14.1.3 - Перемещения в деформируемом твердом теле. Тензор деформаций

Рассмотрим перемещения, возникающие в теле в процессе деформаций. Будем считать, что тело закреплено и его перемещения как недеформируемого жесткого целого исключены.

Пусть некоторая точка А (см. Рис. 14.1.3_1), имевшая до деформации координаты õ, ó è z, вследствие деформации тела оказалась в положении A1 с координатами õ + è, ó + v è z + w. Отрезок AA1 называется линейным перемещением точкиA, а отрезки u, v è w — его проекции на оси координат.

Рисунок 14.1.3_1 - Перемещения в деформируемом теле

923

Глава 14 - Динамика и прочность ГТД

Перемещения и их проекции для разных точек различны; они представляют собой непрерывные функции координат точки

u = f1(x, y, z); v = f2(x, y, z); w = f3(x, y, z).

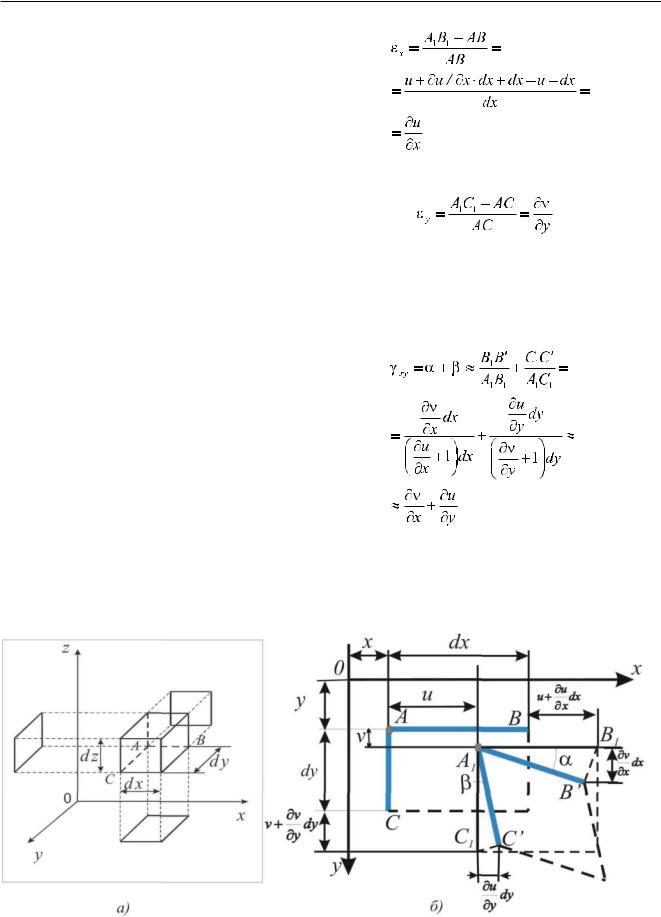
Деформированное состояние в некоторой точ- ке А известно, если известны деформации всех трех проекций элементарного параллелепипеда (см. Рис. 14.1.3_2а). Для этого надо знать относительные линейные деформации трех взаимно перпендикулярных ребер εx, εy èεz и изменения прямых углов между ребрами в плоскостях трех его граней, параллельных плоскостях координат (относительные сдвиги или относительные угловые

деформации γxy, γyz, γzx ).

Найдем зависимости между компонентами деформации и проекциями перемещения на оси координат. Рассмотрим проекцию элементарного параллелепипеда на плоскость õÎó (см. Рис.14.1.3_2б). До деформации координаты точки А - õ è ó, длины проекций ребер dx è dy. После деформации тела точ- ка А перейдет в положение A’, а точка В - в положение B’. Линейное перемещение точки В вдоль оси õ равно сумме линейного перемещения точ- ки А и его приращения, вызванного изменением координаты õ при переходе от точки А к точке В: u + äu/äx·dx . Кроме того, вследствие изменения первоначального прямого угла ВАС на величину α точка В1 займет положение В’. Отрезок В1В’ представляет изменение перемещения v точки А при переходе от точки А к точке В вдоль оси õ. Относительная деформация εx ребра АВ:

(14.1.3-1)

аналогично

Изменение γxy прямого угла ВАС в плоскости õÎó получим, заменив углы α è β их тангенсами и учитывая, что частные производные в скобках малы по сравнению с единицей, получаем:

(14.1.3-2)

Из проекций элементарного параллелепипеда на две другие плоскости координат найдем вы-

Рисунок 14.1.3_2 - Деформация элементарного параллелепипеда

924