Глава 14 - Динамика и прочность ГТД

14.4 - Колебания и вибрационная прочность лопаток осевых компрессоров и турбин

До 60% поломок лопаток ГТД имеют усталостный характер и связаны с действием переменных напряжений при вибрациях. Поломка одной лопатки обычно приводит к лавинообразному процессу повреждения или разрушения других, нарушению балансировки ротора, помпажу и другим серьезным повреждениям двигателя. Для предупреждения вибрационных поломок при проектировании и доводке двигателя исследуются колебания лопаток. Обеспечение вибрационной прочности лопаток регламентируется «Нормами летной годности воздушных судов».

14.4.1 - Свободные и вынужденные колебания лопаток. Собственные ча-

стоты и формы колебаний лопаток

Колебания лопатки в условиях работы на двигателе происходят под действием переменных газодинамических сил, обусловленных, главным образом, неравномерностью газового потока в проточной части. Эти силы изменяются во времени периоди- чески, причем период равен времени одного оборота ротора.

Под действием периодической газодинами- ческой нагрузки лопатка совершает вынужденные колебания. Изменение во времени перемещения U(x,y,z,t) некоторой точки с координатами x,y,z - периодическая функция времени, поэтому ее можно представить в виде суммы гармонических составляющих:

	(14.4.1 -1)
ãäå i	- номер гармоники;
Ui(x,y,z) - амплитуда гармоники;
pi	- частота гармоники;
ϕi	- фаза гармоники;

U0(x,y,z) - средняя величина перемещения. Движение точки при колебаниях можно ин-

терпретировать в соответствии с представлением (14.4.1-1) как сумму движений, происходящих по гармоническому закону.

Если лопатку вывести из положения равновесия (например, ударом) и предоставить действию сил инерции и упругости, исключив внешние нагрузки, она будет совершать свободные колебания относительно исходного положения. Пренебрегая потерями энергии, эти колебания можно рассматривать как незатухающие, а перемещения U(x,y,z,t) - как периодическую функцию времени. При свободных колебаниях, как и в случае вынужденных, перемещения представляют собой сумму гармони- ческих колебаний и могут быть представлены в виде ряда (14.4.1-1) с нулевым средним значением перемещения U0(x,y,z)=0 (свободные колебания происходят вокруг положения равновесия).

Как показано в теории колебаний, и свободные и вынужденные колебания складываются из гармонических составляющих, имеющих одинаковый набор (спектр) частот pi. Эти частоты не зависят ни от способа возбуждения свободных колебаний, ни от внешних нагрузок при вынужденных колебаниях. Они зависят только от материала, формы и размеров самой лопатки и конструкции ее крепления, и поэтому называются собственными.

Функции Ui(x,y,z) в выражении (14.4.1-1) представляют собой распределение амплитуд соответствующих гармонических составляющих. Их можно интерпретировать как изменение формы лопатки при гармонических колебаниях с собственными частотами pi в момент максимального отклонения от положения равновесия. В теории колебаний показано, что при различных способах возбуждения колебаний каждая из этих функций остается неизменной с точностью до постоянного множителя. Таким образом, характер распределения перемещений при гармонических колебаниях лопатки с любой из собственных частот не зависит от способа возбуждения колебаний, от него зависит лишь амплитуда. Закон распределения перемещений, который называют формой колебаний, как и собственная частота, зависит только от материала, формы и размеров лопатки и конструкции ее крепления. Как и собственные частоты, они являются фундаментальным свойством лопатки, поэтому их называют собственными. Каждой собственной частоте колебаний лопатки соответствует своя собственная форма.

Очень важен в практическом отношении такой вид колебаний, когда из всех гармонических составляющих одно имеет амплитуду, значительно превышающую остальные. В этом случае, как видно из (14.4.1-1), все точки лопатки двигаются синхронно по одному и тому же гармоническому закону во времени, одновременно проходя положение равновесия и одновременно достигая мак-

1032

Глава 14 - Динамика и прочность ГТД

симального отклонения. При этом колебания происходят с одной из собственных частот и имеют соответствующую ей собственную форму:

(14.4.1-2)

Такие колебания представляют наибольший практический интерес, поскольку они имеют большие амплитуды. Это происходит потому, что энергия колебаний не раскладывается на несколько слагаемых, соответствующих слагаемым в (14.4.1-1), а концентрируется в одном из них. Именно такие колебания возникают при резонансе. Создавая в специальных экспериментах резонансные режимы колебаний можно наблюдать собственные формы и определять собственные частоты.

Совокупность всех собственных форм колебаний и соответствующих им частот называют собственным спектром лопатки, характеризующим ее вибрационные свойства. Как видно из (14.4.1-1), лопатка, как и любая колебательная система, имеет, вообще говоря, бесконечное множество собственных форм и собственных частот колебаний.

Геометрическое место точек, остающихся неподвижными при гармонических колебаниях называется узловой линией. Узловые линии разделяют поверхность на области, где в каждый момент времени амплитуды вибрационных перемещений

Рисунок 14.4.1_1 - Собственные формы колебаний лопаток а, б, в - первая, вторая и третья

изгибные; г, д - первая и вторая крутильная; е - пластиночная

имеют противоположные знаки. Более высоким собственным частотам соответствуют формы колебаний с большим количеством узловых линий.

При классификации форм колебаний лопаток опираются на представление одиночной лопатки в виде балки или пластинки и преимущественный вид деформации при колебаниях по этой форме. Принято выделять изгибные, крутильные, пластиночные собственные формы.

Изгибные формы колебаний характерны тем, что в лопатке возникают деформации, при которых перпендикулярные оси лопатки сечения не изменяют своей формы, а лишь поворачиваются, оставаясь перпендикулярными к изогнутой оси лопатки. Изгиб происходит вокруг оси наименьшей жесткости сечения. Узловые линии ориентированы перпендикулярно оси лопатки. В зависимости от числа узловых линий различают первую, вторую и т.д. изгибные формы. Первые три формы изгибных колебаний лопатки, жестко закрепленной на диске, показаны на Рис. 14.4.1_1а-в.

Крутильные колебания лопатки совершаются относительно линии центров жесткости попереч- ных сечений. Поперечные сечения поворачиваются без искажения формы (см. Рис. 14.4.1_1г,д). При первой крутильной форме все поперечные сечения лопатки поворачиваются в одну сторону от положения равновесия, имеется одна продольная узловая линия и одна поперечная у корня. При второй крутильной форме верхняя и нижняя части лопатки поворачиваются в противоположных направлениях, поэтому кроме продольной узловой линии имеются две поперечные.

Между крутильными и изгибными формами колебаний существует связь, выражающаяся в том, что при изгибных колебаниях возникают деформации кручения и наоборот. Это происходит из-за несовпадения в общем случае центров масс сече- ний с центрами жесткостей и приводит к возникновению совместных изгибно-крутильных колебаний. Такие формы колебаний особенно характерны при близости собственных частот по изгибным и крутильным формам.

Пластиночные формы колебаний характеризуются тем, что форма поперечного сечения лопатки при колебаниях искажается. Узловые линии располагаются параллельно оси лопатки (см. Рис.14.4.1_1е).

Следует отметить, что описанная классификация форм колебаний условна, перечисленные формы колебаний реализуются в чистом виде только в простейших случаях. Чаще встречаются боле сложные формы колебаний, в которых можно выделить лишь преимущественный вид деформации.

1033

Глава 14 - Динамика и прочность ГТД

Рисунок 14.4.1_2 - Связанные собственные колебания бандажированного рабочего колеса турбины (шесть узловых диаметров)

Колебания бандажированных лопаток являются совместными (связными). Формы таких колебаний более разнообразны, чем в случае одиночных лопаток (см. Рис.14.4.1_2). Различают формы колебаний, при которых сама лопатка имеет один узел

âзаделке и два узла - в заделке и бандаже. Кроме того формы различаются по количеству узловых диаметров. Так, например, при колебаниях с одним узловым диаметром лопатки, расположенные по разные стороны этого диаметра колеблются в противофазе. При колебаниях с двумя узловыми диаметрами в противофазе колеблются лопатки, расположенные в соседних четвертях окружности. Собственная частота связных колебаний тем выше, чем меньше масса и больше жесткость бандажа. Собственные частоты связных колебаний с узлом

âзаделке выше, чем для первой изгибной формы изолированных лопаток. Более подробные сведения о связных колебаниях приведены в [14.8.5].

Наибольший практический интерес собственные формы представляют с точки зрения прогнозирования характера распределения вибронапряжений в лопатке при резонансных колебаниях.

Рисунок 14.4.1_3 - Распределение вибронапряжений (сплошные линии) и перемещений (пунктир) в лопатке

1034

Глава 14 - Динамика и прочность ГТД

При изгибных формах колебаний наибольшие напряжения возникают на входной и выходной кромках и спинке лопатки в сечениях с наибольшим изгибающим моментом. На Рис. 14.4.1_3 показано распределение вибронапряжений в лопатке при колебаниях по первой и второй изгибной формам. Знание форм колебаний позволяет правильно определить места установки датчиков при проведении сложных экспериментов по определению величи- ны вибронапряжений на работающем натурном двигателе.

14.4.2 - Приближенный расчет собственных частот колебаний лопаток

Расчетное определение собственных частот колебаний лопатки является пространственной задачи динамической теории упругости. Для ее решения используются методы и модели, различающиеся точностью, возможностью учета тех или иных особенностей конструкции и условий работы лопатки и, разумеется, трудоемкостью. Рассмотрим два класса моделей: стержневые, пригодные для быстрого приближенного расчета, и наиболее точные и трудоемкие в использовании трехмерные модели.

Стержневые модели используют для приближенных расчетов собственных частот изгибных и крутильных колебаний лопаток. Стержневые модели позволяют с достаточно высокой точностью определять несколько низших собственных частот, они непригодны для анализа пластиночных и смешанных форм колебаний, не позволяют учитывать влияние полок.

В основе этих моделей лежит допущение о том, что напряженное состояние лопатки одноосное. В случае изгибных колебаний принимается по внимание только нормальное напряжение в направлении оси лопатки; оно считается распределенным по сечению лопатки по линейному закону, нейтральная линия при изгибе совпадает с осью наименьшей жесткости корневого сечения. В случае крутильных колебаний аналогичные допущения принимаются относительно касательного напряжения. Расчет собственных частот по стержневой модели сводится к анализу уравнения в частных производных. В аналитическом виде удается определять собственные частоты и формы колебаний лопаток постоянного поперечного сечения без уче- та закрутки профиля и изменения температуры по длине и сечению лопатки.

Для лопаток переменного по длине сечения наиболее простым и, в то же время, достаточно точ-

Рисунок 14.4.2_1 - К расчету собственной частоты колебаний невращающейся лопатки

ным методом определения низшей собственной частоты изгибных колебаний является энергетический метод (метод Рэлея). В его основе лежит идея расчета частоты колебаний по заданной собственной форме; форма колебаний задается априорно, исходя из самых приближенных представлений, а собственная частота рассчитывается с использованием закона сохранения энергии.

Сначала рассмотрим применение метода Рэлея для расчета низшей собственной частоты изгибных колебаний невращающейся лопатки.

Если пренебречь потерями энергии, в любой момент времени сумма кинетической энергии Ê и потенциальной энергии Ï колеблющейся лопатки согласно закону сохранения энергии есть вели- чина постоянная:

Ê + Ï = const

(14.4.2-1)

В положении равновесия потенциальная энергия равна нулю, а кинетическая энергия достигает максимума Êmax. В положении максимального отклонения от равновесия, наоборот, кинетическая энергия равна нулю, а потенциальная - максимальна Ïmax. Следовательно

Êmax = Ïmax.

(14.4.2-2)

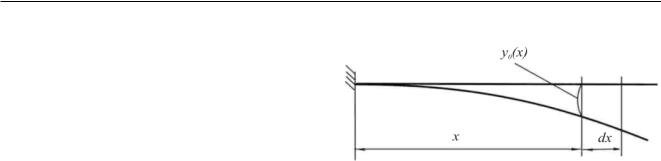
Для определенности будем рассматривать лопатку как консольно закрепленный стержень длиной L (см. Рис.14.4.2_1) с плотностью материала ρ, модулем упругости E, изменяющимися по длине площадью сечения F(x) и моментом инерции I(x). Рассматриваем гармонические колебания с круговой собственной частотой ð.

Перемещения произвольной точки оси лопатки с координатой x задаем в виде произведения гармонической функции времени на функцию y0(x), которая представляет собой распределение амплитуд колебаний по координате, то есть форму колебаний:

1035

Глава 14 - Динамика и прочность ГТД

y(x,t) = y0(x) cos pt.

(14.4.2-3)

Форму колебаний y0(x) будем считать извест-

íîé.

Для элемента лопатки dx (см. Рис.14.4.2_1) максимальная кинетическая энергия равна

Для всей лопатки максимальная кинетическая энергия определяется интегрированием

(14.4.2-4)

Потенциальная энергия лопатки в момент максимального отклонения от положения равновесия определяется известным из сопротивления материалов соотношением для потенциальной энергии изогнутого стержня:

(14.4.2-5)

ãäå M(x) - изгибающий момент, соответствующий прогибу y(x), который в соответствии с уравнением изогнутой оси стержня равен:

(14.4.2-6)

Подставляя (14.4.2-6) в (14.4.2-5) и получившееся выражение для потенциальной энергии вместе с (14.4.2-4) в уравнение (14.4.2-2), находим круговую собственную частоту

(14.4.2-7)

По аналогии с (14.4.2-7) методом Рэлея может быть получено соотношение для первой собственной частоты крутильных колебаний [14.8.13]:

(14.4.2-8)

ãäå ϕ(x) - приближенная форма крутильных колебаний.

Форма колебаний в методе Рэлея задается априорно, она лишь должна удовлетворять гранич- ным условиям. Для изгибных колебаний, например, это отсутствие перемещений и поворота сечения в заделке (корневом сечении):

(14.4.2-9)

Получающиеся методом Рэлея приближенные значения собственных частот всегда выше точных и тем ближе к ним, чем ближе к действительной заданная приближенно собственная форма. Практика расчетов показывает, что соотношение (14.4.2-7) дает достаточно точные результаты, если форму колебаний принимать совпадающей с функцией прогибов от равномерно распределенной статической нагрузки. При применении метода Рэлея можно с достаточной для практических расчетов точ- ностью получать только частоты колебаний по первой изгибной и первой крутильной формам. Для более высоких собственных частот формы колебаний более сложны, и априорно задать их с достаточной точностью трудно.

Для стержня постоянного по длине сечения из теории колебаний известны соотношения для расчета собственных частот изгибных и крутильных колебаний. Приведем их без вывода (см., например, [14.8.20]).

(14.4.2-10)

1036

Глава 14 - Динамика и прочность ГТД

Рисунок 14.4.2_2 - К расчету собственной часто-

	ты колебаний вращающейся ло-
	патки
ãäå pi è pkði	- круговые частоты изгибных
	и крутильных колебаний по i-é
Å è ρ	собственной форме;
	- модуль упругости и плотность
	материала лопатки;

G=E/2(1+µ) - модуль сдвига;

µ- коэффициент Пуассона;

L		- длина лопатки;
F0	è I0	- площадь и момент инерции
		сечения относительно оси наи-
Ik0	è Ip0	меньшей жесткости;
		-момент инерции при кручении
		и полярный момент инерции се-
		чения.

В соотношениях (14.4.2-10) αi è βi - коэффициенты, зависящие от номера собственной формы i. Для изгибных колебаний стержня постоянного сечения с консольным креплением αi=3,515; α2=22,033; α3=61,701.

Соотношения (14.4.2-10) можно использовать для расчета собственных частот изгибных и крутильных колебаний лопаток постоянного по длине сечения. Соотношения (14.4.2-7) и (14.4.2-8) для лопаток переменного сечения можно привес-

ти к виду (14.4.2-10), считая геометрические характеристики относящимися к корневому сечению. Коэффициенты αi в этом случае имеют другие значе- ния, зависящие от закона изменения размеров сечения по длине лопатки.

Теперь рассмотрим расчет собственных частот изгибных колебаний вращающейся лопатки. Рабочие лопатки совершают колебания в поле центробежных сил. Это приводит к изменению собственных частот, которые принято называть динамическими, в отличие от статических собственных частот невращающейся лопатки.

На Рис. 14.4.2_2 показана схема нагружения колеблющейся лопатки. Центробежная сила dPö, действующая на элемент лопатки dx, при отклонении лопатки от положения равновесия вызывает появление изгибающего момента, стремящегося вернуть лопатку в положение равновесия. Это эквивалентно повышению изгибной жесткости лопатки и ведет к тому, что динамические собственных частот оказываются выше соответствующих статических. Различие тем больше, чем выше частота вращения ротора и больше центробежные силы.

Для количественной оценки этого эффекта рассмотрим низшую собственную частоту изгибных колебаний вращающейся лопатки. Воспользуемся описанным выше для невращающейся лопатки приближенным методом Рэлея.

Как и в случае невращающейся лопатки перемещения произвольной точки оси лопатки с координатой x задаем в виде произведения гармонической функции времени на форму колебаний y0(x). Закон сохранения энергии приводит к равенству максимальных значений кинетической и потенциальной энергии (14.4.2-2).

Однако в случае вращающейся лопатки потенциальная энергия состоит из двух составляющих: энергии упругой деформации Ïmax (14.4.2-5) и работы центробежных сил W, которая должна быть совершена при переходе лопатки из положения равновесия в положение максимального отклонения:

Êmax = Ïmax + W. (14.4.2-11)

Центробежная сила dPö, действующая на элемент лопатки dx, совершает при отклонении лопатки от положения равновесия работу на перемещении e (см. Рис. 14.4.2_2). Ввиду малости угла δ будем считать, что сила dPö и ее проекция на ось x равны (проекцию также будем обозначать dPö ). Работой проекции силы dPö íà îñü y пренебрежем ввиду малости угла δ.

1037