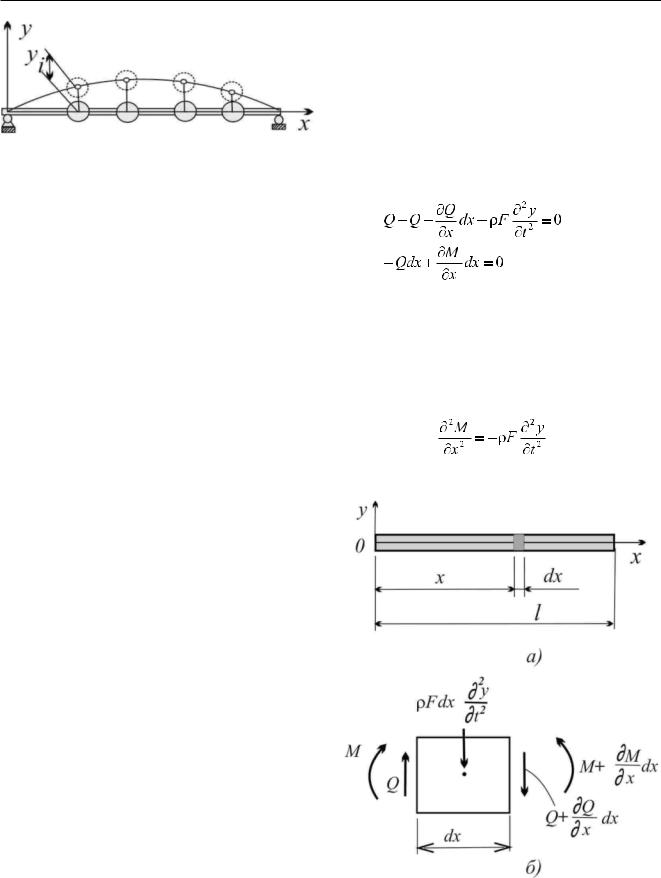
Глава 14 - Динамика и прочность ГТД

Рисунок 14.1.20_4 - Колебания упругой системы с n степенями свободы

Составляя выражения прогиба для всех n масс, придем к системе однородных уравнений, аналогичной (14.1.20-3), которую удобно записать в матричной форме:

(p2 [α	m	] - [E]) {y	} = 0	(14.1.20-8)
ij	j	0

ãäå [E] - единичная матрица порядка n; {y0} - вектор амплитудных прогибов.

Частотное уравнение получается после приравнивания нулю определителя системы:

| p2 [α	m	] - [E]| = 0	(14.1.20-9)
ij	j

Уравнение (14.1.20-9) дает значения n собственных частот колебаний p1, p2…pn, и каждой ча- стоте соответствует своя форма колебаний. С математической точки зрения, отыскание собственных частот и форм колебаний системы с конечным числом степеней свободы сводится к расчету собственных чисел и векторов матрицы (14.1.20-9).

Если на колебательную систему с n степенями свободы действует нагрузка, изменяющаяся во времени по гармоническому закону с частотой Ω, система может иметь n резонансных режимов при совпадении этой частоты с любой из собственных частот. Условие резонанса имеет вид:

Ω = pk , k = 1,2,3,…n

(14.1.20-10)

14.1.21 - Колебания системы с распределенной массой

В качестве примера системы с непрерывно распределенной массой рассмотрим стержень, изготовленный из материала с плотностью ρ (напомним, что в предыдущих разделах стержень считался невесомым). Рассмотрим изгибные колебания стержня (см. Рис. 14.1.21_1а). Масса, приходящаяся на единицу длины стержня равна ρF (ãäå F-

площадь поперечного сечения стержня, вообще говоря, не постоянная по его длине).

Будем считать, что стержень имеет плоскость симметрии xOy, и колебания происходят в этой плоскости. На Рис. 14.1.21_1б показан малый элемент стержня длиной dx, а также внешние и внутренние силы, действующие на него. Условия равновесия сил на ось y и условие равенства моментов имеют вид:

(14.1.21-1)

ãäå Q - перерезывающая сила;

M - изгибающий момент.

Выражая Q из второго уравнения и подставляя в первое, получаем:

(14.1.21-2)

Рисунок 14.1.21_1 - Колебания стержня с распределенной массой

961

Глава 14 - Динамика и прочность ГТД

Воспользуемся известным из сопротивления материалов уравнением изогнутой линии балки:

(14.1.21-3)

ãäå E - модуль упругости материала;

I - момент инерции поперечного сечения стержня.

Подставляя (14.1.21-3) в (14.1.21-2) получаем уравнение изгибных колебаний стержня:

(14.1.21-4)

Таким образом, исследование колебаний стержня с распределенной массой сводится к анализу дифференциального уравнения четвертого порядка в частных производных.

В случае стержня постоянного сечения это уравнение имеет постоянные коэффициенты и несколько упрощается:

(14.1.21-5)

ãäå

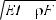
Уравнение колебаний должно быть дополнено начальными и граничными условиями.

Рассмотрим собственные частоты и формы колебаний на примере стержня постоянного поперечного сечения. При колебаниях стержня с одной из собственных частот p, его прогибы в некоторой произвольной точке изменяются во времени по гармоническому закону:

y(x,t) = X(x)·(Acos pt + B sin pt) (14.1.21-6)

ãäå X(x) - неизвестная функция координаты, задающая распределение амплитуд колебаний по длине стержня;

À, Â - коэффициенты, определяются начальными условиями.

Подставляя в (14.1.20-8) получаем уравнение для неизвестной функции X(x)

(14.1.21-7)

Решение этого уравнения позволяет определить неизвестную функцию X(x), если заданы гранич- ные условия.

Рассмотрим решение на примере стержня, свободно опертого по концам. В этом случае уравнение (14.1.21-7) дополняется граничными условиями равенства нулю перемещений и изгибающих моментов на концах стержня при x = 0 è x = L. Равенство нулю изгибающих моментов в соответствии с (14.1.21-3) сводится к равенству нулю вторых производных перемещения на концах стержня:

y(0) =y(L) = 0,

(14.1.21-8)

Этим условиям и уравнению (14.1.21-7) соответствует семейство функций (вывод опускаем, можно проверить подстановкой):

Xk(x) = sin(kπx / L), k = 1, 2, 3... (14.1.21-9)

Подставляя в (14.1.21-7) получаем, что каждому зна- чению k соответствует своя собственная частота:

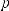
, k = 1, 2, 3... (14.1.21-10)

Соответствующий этой частоте период колебаний равен:

(14.1.21-11)

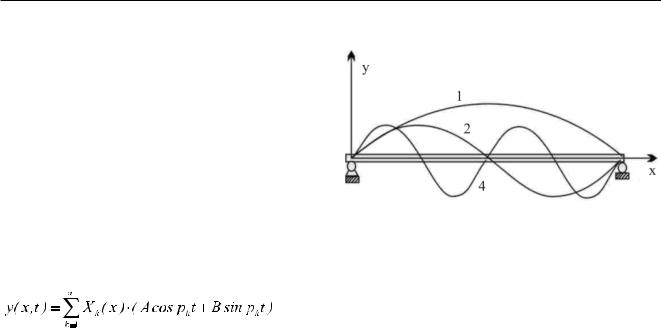
Отсюда видно, что система с распределенной массой имеет бесконечное количество собственных частот и форм колебаний; каждой собственной частоте соответствует своя форма. Спектр собственных частот представляет собой бесконечный дискретный ряд значений. Несколько низших собственных форм колебаний рассматриваемого стержня приведены на Рис. 14.1.21_2 (цифрами обозначены номера соответствующих собственных частот).

962

Глава 14 - Динамика и прочность ГТД

Анализ собственных частот и форм колебаний стержней с другими граничными условиями, а также стержней переменного сечения можно найти, например, в [14.8.9].

Подстановка (14.1.21-9) в (14.1.21-6) дает бесконечное множество частных решений уравнения колебаний (14.1.21-5):

yk(x,t) = Xk(x) (A cos pkt + B sin pkt), k = 1,2,3…

Путем сложения частных решений можно представить любые поперечные колебания стержня:

(14.1.21-12)

Знание собственных форм колебаний позволяет определить распределение напряжений в теле в момент максимального отклонения от положения равновесия и, благодаря этому, определить опасные точки и сечения при резонансных колебаниях по той или иной форме.

Можно показать, что если на стержень с распределенной массой действует нагрузка, изменяющаяся во времени по гармоническому закону с частотой Ω, система может иметь бесконечное число резонансных режимов при совпадении этой частоты с любой из собственных частот. Условие резонанса имеет вид:

Ω = pk, k = 1,2,3... (14.1.21-13)

Возможна ситуация, когда при выполнении этого условия резонанс не возникает. Это возможно, например, если сосредоточенная переменная сила приложена в точке, которая при соответствующей форме колебаний не имеет перемещения. Такие точки называются узлами. Напротив, если переменная сила приложена в зоне, где при соответствующей форме колебаний перемещения велики, резонансный режим наиболее опасен.

Колебания системы с распределенной массой рассмотрены выше на примере поперечных колебаний стержня в одной их плоскостей симметрии профиля. Положенные в основу стержневой модели допущения (одноосное напряженное состояние, гипотеза плоских сечений) выполняются с достаточной точностью лишь в случаях, когда один из размеров тела значительно превышает остальные

Рисунок 14.1.21_2 - Собственные формы колебаний свободно опертого стержня

размеры. Применительно к анализу колебаний существует еще одно ограничение – стержневые модели непригодны для расчета высших собственных частот колебаний. В этих случаях необходимо использовать трехмерные модели и численные методы, например, метод конечных элементов.

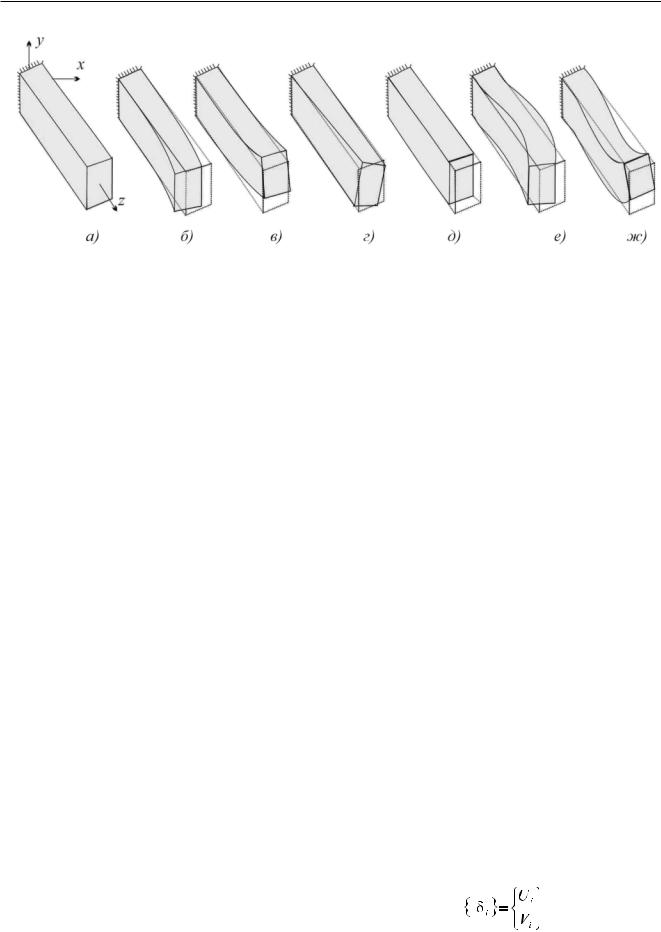
Для того, чтобы продемонстрировать ограни- ченность стержневых моделей, рассмотрим несколько собственных форм, получающихся при трехмерном анализе колебаний призматического стержня прямоугольного сечения (см. Рис. 14.1.21_3). Приведены первые изгибные формы колебаний в плоскостях xOz è yOz (см. Рис. 14.1.21_3б,в), первая крутильная форма (г) и форма продольных колебаний (д), а также вторая изгибная форма колебаний в плоскости xOz è yOz (е и ж). Название форм определяется характером деформации тела в положении максимального отклонения от положения равновесия. При приведенных собственных формах форма поперечного сечения в процессе колебаний не искажается, поперечные сечения лишь перемещаются (д) или поворачиваются вокруг осей x è y при изгибных колебаниях, z – при крутильных. Более высоким собственным частотам соответствуют более сложные изгибные и крутильные, а также смешанные формы.

Следует отметить, что приведенный выше модальный анализ (так называют анализ собственных частот и форм колебаний) с использованием стержневой модели показал лишь изгибные формы колебаний и только в одной плоскости. Трехмерный анализ более трудоемок, но дает значительно больше информации о возможных резонансных режимах. Низшие собственные частоты колебаний с достаточной для инженерных расчетов точностью определяются на базе стержневых моделей. Для расчета высших собственных частот необходимо использовать трехмерные модели.

963

Глава 14 - Динамика и прочность ГТД

Рисунок 14.1.21_3 - Низшие собственные формы колебаний призматического стержня (результаты трехмерного модального анализа)

14.1.22 - Концепция метода конеч- ных элементов

Анализ напряженно-деформированного состояния и колебаний деталей ГТД в ответственных случаях требует решения краевых задач механики деформируемого твердого тела. В силу сложности формы деталей использовать аналитические методы решения таких задач не удается, и приходится прибегать к численным методам. Наиболее распространенным в инженерной практике решения задач прочности и колебаний стал метод конечных элементов (МКЭ), реализованный в компьютерных системах инженерного анализа. Его основные достоинства: универсальность, широкий круг решаемых задач (статика, динамика, устойчивость, упругость, пластичность, ползучесть, контактные задачи, температурные напряжения и т.д.), простота алгоритмизации.

В общих чертах, идея метода конечных элементов состоит в следующем.

-Исследуемая деталь (тело) разбивается воображаемыми линиями или поверхностями на большое число конечных элементов простой формы (призмы, пирамиды, треугольники и т.д.), размеры которых значительно меньше размеров тела.

-Перемещение в любой произвольной точке конечного элемента однозначно определяется че- рез перемещения в его вершинах (узловых точках)

ñпомощью функции перемещений. Она выбирается линейной, параболической и т.д. таким образом, чтобы обеспечить необходимую точность аппроксимации перемещений и напряжений внутри элемента.

-Заданное с помощью функции перемещений поле перемещений внутри элемента дает возможность выразить деформации и напряжения внутри элемента через узловые перемещения. Например, при линейной аппроксимации перемещений деформация и напряжение в каждом элементе получаются постоянными.

-Задача, состоявшая в решении системы дифференциальных уравнений в частных производных, сводится к решению системы алгебраических уравнений и отысканию перемещений в узловых точках. Эта процедура перехода от неизвестных функций к неизвестным их значениям в отдельных узловых точках называется дискретизацией.

-Перемещения в узлах определяются из условий равновесия системы конечных элементов под действием приведенных к узлам внешних сил.

-По найденным узловым перемещениям определяются поля напряжений и деформаций в элементах и детали в целом.

Рассмотрим эту процедуру на самом простом примере расчета плоского напряженного состояния

âупругом теле. Исследуемая конструкция представляет собой пластинку, нагруженную внешними силами на границе (см. Рис. 14.1.22_1) и закрепленную в нескольких точках.

Исследуемую область разобьем на треугольные

элементы (см. Рис. 14.1.22_1), узлы типичного элемента e обозначим i, j, m. Перемещения δ â i-м узле имеют две составляющие (проекции на оси x и y)

,

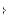964

Глава 14 - Динамика и прочность ГТД

а вектор всех перемещений в элементе выглядит как:

.

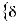
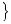
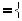
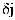
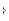Примем простейшую линейную аппроксимацию перемещений внутри элемента (х, у - координаты в пределах элемента):

U = α1 + α2x + α3y;

V = α4 + α5x + α6y, (14.1.22-1)

ãäå α1…α6 - коэффициенты аппроксимации.

Для их определения подстановкой в (14.1.22-1) координат и перемещений узловых точек составляются две системы по три уравнения. Например, одна из них для перемещений в направлении оси õ имеет вид:

(14.1.22-2)

ледовательности i, j, m.

Общая деформация в любой точке элемента для случая плоского напряженного состояния имеет вид:

(14.1.22-4)

Продифференцировав уравнения (14.1.22-1) и (14.1.22-2), получаем в матричном виде:

{ε} = [B] {δ}e,

(14.1.22-5)

где матрица узловых координат:

.

Решая их, получим для перемещений U è V внутри элемента выражения:

Обобщенный закон Гука, выражающий связь между напряжениями и деформациями при упругом поведении материала, с учетом тепловых деформаций имеет вид (см. раздел 14.1.19):

(14.1.22-3)

ài = xjym - xmyj; bi = yj - óm; ñi = xm - xj,

ãäå ∆ - площадь треугольника ijm. Коэффициенты a, b, ñ с индексами j è m получа- ются циклической перестановкой индексов в пос-

{σ} = [D] ({ε} - {ε0})

(14.1.22-6)

ãäå {ε0} - вектор начальной тепловой деформации; [D] - матрица упругости материала, которая

для изотропного материала и плоского напряженного состояния имеет вид:

(14.1.22-7)

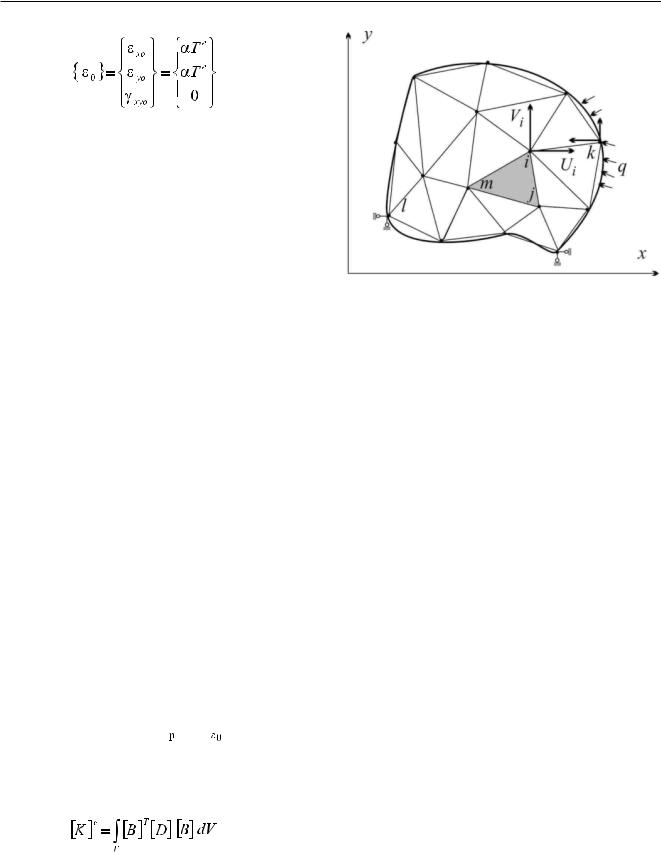
Вектор тепловой деформации имеет вид:

965

Глава 14 - Динамика и прочность ГТД

(14.1.22-8)

ãäå α - коэффициент линейного расширения; Te - температура элемента.

Подставляя (14.1.22-5) в (14.1.22-6), получим соотношение для расчета напряжений в элементе по известным узловым перемещениям:

{σ} = [D][B]{δ}e – [D]{ε	})	(14.1.22-9)
0

Внешние силы, действующие на тело, можно разделить на две категории: массовые (или объемные) и поверхностные силы. Массовые силы характеризуются силой, приходящейся на единицу массы (или объема) тела. Пример массовых сил - центробежные силы. Поверхностные силы действуют на поверхности тела (см. Рис. 14.1.22_1), они обусловлены воздействием контактирующих тел или окружающей среды; пример поверхностных сил - давление жидкости или газа.

В узлах конечно-элементной сетки действуют три группы сил. Первая группа - силы, стати- чески эквивалентные внешним поверхностным и массовым силам {F}ep, они получаются интегрированием внешних сил по поверхности или объему и распределению их между соответствующими узлами. Вторая группа - силы, возникающие от на- чальной деформации {F}eε0.Третья группа – силы, пропорциональные узловым перемещениям {δ}e. Вектор узловых сил в элементе {F}e включает в себя по две силы в каждом узле:

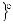
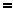
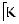
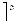
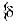
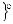
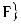
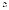
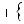
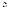, (14.1.22-10)

ãäå [K]e – матрица жесткости элемента

(14.1.22-10)

ãäå V – объем элемента.

Çíàê [ ]Ò означает транспортирование матрицы (строки и столбцы матрицы меняются местами).

Просуммировав узловые силы по всем элементам, получают систему алгебраических урав-

Рисунок 14.1.22_1 - Разбиение исследуемой области на конечные элементы

нений относительно неизвестных узловых перемещений {δ}:

[K] {δ} = {F},

(14.1.22-11)

ãäå [K] - матрица жесткости системы;

{F} - вектор внешних нагрузок (включая тепловые).

Система (14.1.22-11) включат в себя N = zns линейных алгебраических уравнений. Здесь n – число узлов конечно-элементной сетки, z – число степеней свободы в каждом узле (в плоской задаче z = 2), s – число степеней свободы по которым перемещения известны (закрепленные узлы, например).

Решение системы (14.1.22-11) позволяет определить перемещения узловых точек {δ}, а по ним - деформации и напряжения в элементах рассчитываемой конструкции.

Соотношения метода конечных элементов для трехмерного напряженно-деформированного состояния аналогичны рассмотренным выше. Конеч- ные элементы в трехмерном случае представляют собой объемное тело (призмы, пирамиды), число степеней свободы в каждом узле – три.

14.1.23 - Реализация метода конеч- ных элементов в инженерных рас-

четах

Соотношения (14.1.22-1) - (14.1.22-6), определяющие свойства элементов, были записаны в простейшем виде. При проведении расчетов часто используют элементы с более сложными свойствами.

966

Глава 14 - Динамика и прочность ГТД

Возможно, в частности, использование вместо линейной аппроксимации перемещений в элементе (14.1.22-2) функции перемещений в виде полинома второго порядка. Такие элементы называются элементами второго порядка и имеют дополнительные узлы в серединах сторон. Их использование приводит к более сложным соотношениям, но позволяет при том же количестве элементов существенно повысить точность результатов.

Соотношения между напряжениями и деформациями, записанные в (14.1.22-6) в виде обобщенного закона Гука, также могут быть более сложными и учитывать анизотропию свойств материала, пластические деформации, ползучесть.

При моделировании трехмерного напряжен- но-деформированного состояния деталей авиационных двигателей используют объемные конечные элементы первого и второго порядка в виде 6-гран- ника (гексаэдра).

Элемент первого порядка определен восьмью узлами и имеет по три степени свободы в каждом узле, которые представляют собой поступательные перемещения в направлениях координатных осей x, y, и z. Для такого элемента возможно задание пластических свойств и ползучести. Элемент второго порядка также имеет форму шестигранника, но отличается большим количеством узлов – 20. В пакете ANSYS (см.ниже) наиболее широко использующийся элемент первого порядка имеет название SOLID45, второго порядка - SOLID95.

Построение конечноэлементной модели – один из наиболее ответственных этапов проведения расчетов методом конечных элементов, определяющий, наряду с принятыми граничными условиями, достоверность получаемых результатов.

Конечно-элементная модель характеризуется типом применяемых конечных элементов и густотой разбивки (размером элементов) в конкретных зонах. В одной модели могут быть применены разные типы элементов, выбор которых зависит от целей расчетного исследования, сложности геометрической модели, возможностей вычислительной техники и опыта исполнителя.

Густота разбивки конечноэлементной модели определяется одним общим правилом: в зонах ожидаемой концентрации напряжений сетка элементов должна сгущаться. Рекомендуемый характерный размер элемента в зоне концентрации должен быть примерно на порядок меньше типичного размера самого концентратора. Например, для описания конечноэлементной моделью галтели радиусом 2 мм необходимо применять элементы со стороной около 0,2 мм. Отметим, что применение конечных элементов второго порядка по-

зволяет получить приемлемую точность результатов относительно меньшим количеством элементов. При построении сеток следует избегать использования элементов с большим отношением размеров.

При моделировании тонкостенных деталей следует иметь в виду, что при их изгибе градиент напряжений по толщине может быть большим (растяжение на одной поверхности и сжатие на другой), следовательно, конечно-элементная сетка должна иметь несколько слоев элементов по толщине. В ряде случаев для таких конструкций рекомендуется использование специальных элементов в форме четырехугольного элемента криволинейной оболочки. В таких элементах используется специальная аппроксимация перемещений по толщине, позволяющая описывать деформацию изгиба в одном слое элементов.

Широкое применение метода конечных элементов в инженерных расчетах началось с появлением достаточно мощной вычислительной техники в начале 70-х годов. Уже тогда удавалось успешно моделировать напряженно-деформиро- ванное состояние и колебания ответственных деталей авиационных двигателей. К тому же времени относится развитие коммерческих программных продуктов, проводящих вычисления на основе метода конечных элементов.

В настоящее время существуют мощные программные комплексы, позволяющие решать не только задачи динамики и прочности конструкций, но и задачи гидродинамики, акустики, электромагнетизма, оптимизации и др. Наиболее известными являются: ANSYS (фирма-разработчик EDS, USA), NASTRAN (MSC Software, USA),ABAQUS (Hibbit, Karlsson&Sorensen Inc, USA), MARC (MSC Software, USA), I-DEAS (EDS, USA), Samcef (Samtech, Бельгия), LS–DYNA(EDS, USA). Эти программы близки по набору основных реализованных в них возможностей. Перечислим некоторые из них.

-Решение задач в одномерной, двумерной

èтрехмерной постановках. Наличие обширной библиотеки элементов различной формы с различ- ными функциями перемещений.

-Анализ статического и динамического напря- женно-деформированного состояния, модальный анализ, решение задач устойчивости конструкций, расчет стационарных и нестационарных тепловых полей, решение задач гидродинамики, электромагнитных полей и акустики.

-Реализация различных моделей поведения материалов: упругости, пластичности, ползучести с зависящими от температуры свойствами матери-

967

Глава 14 - Динамика и прочность ГТД

алов. Моделирование поведения конструкций из композиционных материалов.

-Решение задач оптимизации конструкций

ñдостаточно широкими возможностями выбора целевых функций и назначения ограничений.

-Специальные возможности для анализа нелинейных быстропротекающих процессов, таких как обрыв лопатки, или попадание птицы в авиадвигатель.

-Интерактивная работа с пользователем. Развитые средства построения геометрических и ко- нечно-элементных моделей, задания нагрузок, визуализации и обработки результатов расчетов.

-Наличие интерфейсов передачи геометрических моделей из систем автоматизированного проектирования и инженерных расчетов.

-Возможность дополнения пакета собственными элементами, критериями пластичности и разрушения и т.д., наличие языка макрокоманд, позволяющего пользователю разрабатывать собственные приложения.

Хотя список возможностей пакетов, в принципе, одинаков, есть и определенные отличия. В частности, в MARC изначально уделялось большое внимание моделированию технологических процессов штамповки, гибки и т.д. Пакет I-DEAS имеет специальные возможности обработки экспериментальных данных и идентификации результатов расчетов. В состав Samcef включен специальный модуль расчета динамики роторов. Видимо этими отличиями объясняется использование ведущими зарубежными фирмами сразу нескольких конечноэлементных пакетов. Например, на UTC используются ANSYS и NASTRAN; Snecma и MTU применяют NASTRAN, ABAQUS, Samcef; на Boeing - ANSYS, ABAQUS; Rolls-Royce использует ABAQUS и NASTRAN.

14.1.24 - Пример анализа напряженного состояния тела в трехмерной постановке методом конечных элементов. Концентрация напряжений в упругом и упруго-пластичес- ком теле

Результаты анализа напряженно-деформиро- ванного состояния методами теории упругости и п- ластичности в трехмерной (или двумерной) постановке ряде случаев существенно отличаются от результатов, получаемых в одномерной постановке методами сопротивления материалов. Причина

– в допущениях, принимаемых в рамках использу-

Рисунок 14.1.24_1 - Расчетная схема

емой в сопротивлении материалов стержневой модели. Напомним их: напряженное состояние счи- тается одноосным; отличной от нуля считается только одна компонента тензора напряжений – нормальное напряжение, направленное вдоль оси стержня; закон распределения этой компоненты по се- чению стержня считается линейным.

Рассмотрим в качестве примера задачу об изгибе консольного стержня равномерно распределенной нагрузкой q (см. Рис. 14.1.24_1). Стержень имеет ступенчатое сечение, в сечении A1B1C1 имеется галтель. Стержень жестко защемлен с левого конца, длина его тонкой части 50 мм, толстой – 50 мм. Размеры поперечного сечения в тонкой ча- сти: ширина b = 10 мм, высота h = 10 мм. В толстой части b = 10 мм, высота h = 20 мм. Радиус скругления в галтели 2 мм. На верхней поверхности приложена равномерно распределенная нагрузка интенсивностью q = 10 МПа, что при соответствует нагрузке на единицу длины (погонной) 105 Н/м. Материал стержня упруго-пластический, диаграмма σ-εприведена на Рис. 14.1.24_2. Модуль упругости E = 217500 МПа, предел текучести

σ0.2 = 430 ÌÏà.

Решение в рамках стержневой модели дает для изгибающего момента M :

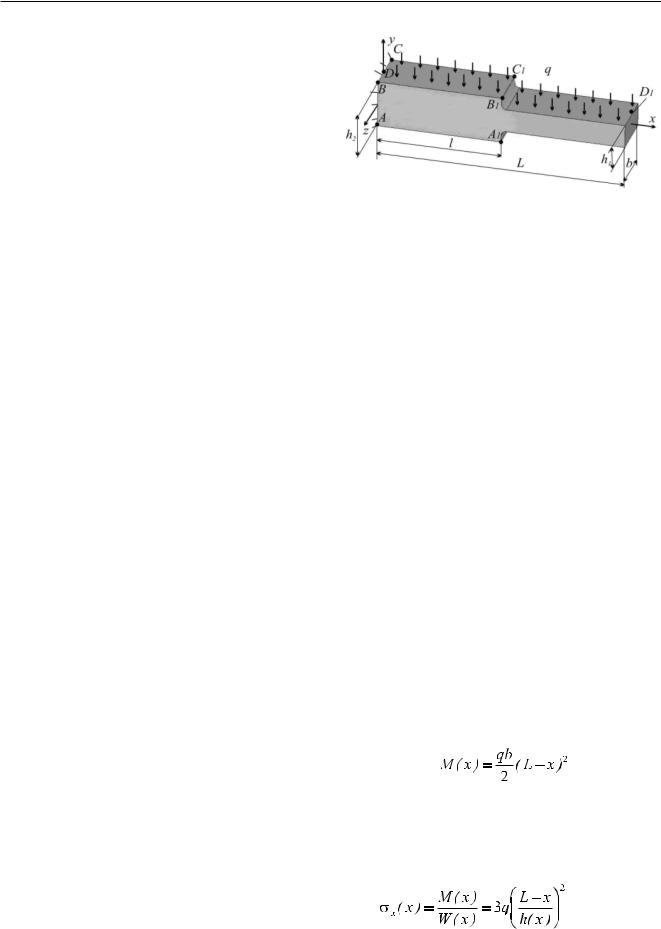
Учитывая, что момент сопротивления прямоугольного сечения равен W = 1/6 bh2 , для напряжения на верхней поверхности σz получаем:

968

Глава 14 - Динамика и прочность ГТД

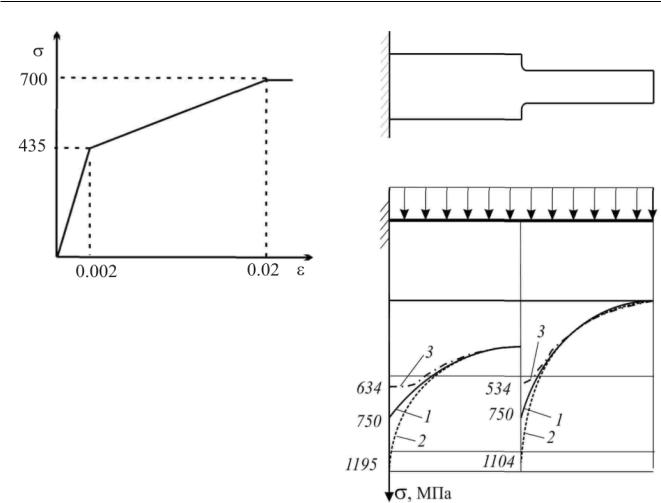
Рисунок 14.1.24_2 - Модель материала

Распределение этого напряжения по линии DD1 показано на Рис. 14.1.24_3 (кривая 1). Максимальное напряжение растяжения возникает в заделке и на линии B1C1, оно равно 750 МПа.

Анализ трехмерных полей напряжений и деформаций в стержне проводили с помощью метода конечных элементов. Конечно-элементная модель состояла из 9000 объемных двадцатиузловых элементов первого порядка и имела около 500 000 степеней свободы. Результаты расчета в виде полей компоненты напряжения σx и деформации εx приведены на Рис. 14.1.24_4.

На первом этапе анализ проводился без учета пластических деформаций, в упругой постановке. Расчеты показали, что напряженное состояние существенно отличается от полученного выше по стержневой модели лишь вблизи заделки и галтели (см. Рис. 14.1.24_4,а). Так, в частности, в галтели имеет место концентрация напряжений с теоретическим коэффициентом концентрации 1, 47, а в заделке – с коэффициентом 1,59. В заделке наиболее напряженными оказываются угловые точки на верхней поверхности, в этих точках напряженное состояние не одноосное, это всестороннее растяжение.

С измельчением сетки конечных элементов напряжения в концентраторах заделке возрастают. Так проявляется погрешность приближенного рас- чета методом конечных элементов, которая снижается с уменьшением размера элементов в зоне больших градиентов напряжений. Достаточно мелкой считают сетку, при которой напряжения перестают зависеть от размера элементов. В рассматриваемом примере в зоне галтели такая ситуация

Рисунок 14.1.24_3 - Напряжения в стержне

достигнута при параметрах сетки, указанных выше, т.е. приведенное значение коэффициента концентрации напряжений в галтели определено с достаточной для практических целей точностью. Иной оказывается ситуация в заделке. Неоднократное измельчение сетки в этой области не приводит к стабилизации напряжений. Это связано с особенностью напряженного состояния, которая состоит в том, что теоретически напряжения в жесткой заделке асимптотически стремятся к бесконечности при любой отличной от нуля нагрузке. С точки зрения практической прочности такой результат бесполезен, поскольку применение обычных критериев прочности невозможно.

Напряжения существенно превосходят предел текучести материала (см. Рис. 14.1.24_3), поэтому был проведен расчет с учетом пластических деформаций. Он показал следующее. Поле напряжений (см. Рис. 14.1.24_4б) отличается от упругого решения в локальной области вблизи концентраторов: галтели и заделки. Непосредственно вблизи концентраторов появились пластические зоны. За пре-

969

Глава 14 - Динамика и прочность ГТД

Рисунок 14.1.24_4 - Поля напряжений а) поле упругих напряжений; б) поле напряжений с учетом пластичности; в) зоны пластичности

делами пластической зоны напряжения несколько выше, чем в упругом решении, это эффект перераспределения напряжений. Напряжения оказались ниже, чем в расчете по стержневой модели, поэтому использовать коэффициент концентрации напряжений в качестве характеристики локального напряженного состояния нельзя.

Деформации в зонах концентрации напряжений стала существенно выше, чем в упругом решении. В зоне заделки суммарная деформация составила 0,0085, в том числе пластическая 0,0061. Этот эффект называется концентрацией деформаций. Зоны пластичности в стержне локализованы, поэтому перемещения мало отличаются от упругих.

Таким образом, трехмерная постановка зада- чи и метод конечных элементов позволяют детально исследовать напряженное состояние в зонах концентрации напряжений. Однако, если напряжения в этих зонах превышают предел текучести ма-

териала, в детали появляются пластические зоны, вблизи которых расчет напряжений в упругой постановке дает существенные погрешности. Именно локальные пластические деформации в зоне концентрации напряжений и деформаций при циклическом нагружении могут стать причиной разрушения деталей по механизму малоцикловой усталости.

970