Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.4_3 - Критические режимы несимметричного ротора

14.5.5 - Ротор с распределенными параметрами

Модель одномассового ротора, у которого массой вала в сравнении с массой диска можно пренебречь, позволяет понять поведение неуравновешенного ротора при его колебаниях. Здесь воспроизводится резонансное возрастание амплитуды вблизи критического режима, явление самоцентрирования ротора на закритических частотах вращение, повышение критической частоты в связи с влиянием гироскопического эффекта, влияние демпфирования и жесткости опор. В то же время, для определения критических частот вращения реальных роторов с приемлемой для практики точ- ностью такая модель в ряде случаев оказывается слишком упрощенной.

В роторах современных ГТД из-за облегчения дисков масса вала оказывает значительное влияние на колебания. Для анализа такой колебательной системы необходимо учитывать распределение массы по длине ротора, т.е. рассматривать ротор как систему с распределенными параметрами. Особенность роторов с распределенными параметрами состоит в том, они обладают бесконечным количеством (спектром) собственных частот и форм колебаний и соответствующих критических частот вращения. Однако, определять весь спектр критических частот нет необходимости - для практических целей достаточно найти несколько низших критических частот, располагающихся внутри или вблизи диапазона рабочих частот вращения ротора.

Рисунок 14.5.5_1 - Ротор с распределенными параметрами

Для вывода уравнений колебаний ротора с распределенными параметрами введем следующую схематизацию.

Будем полагать, что продольный размер ротора - его длина вдоль оси вращения - существенно превышает поперечные размеры. Тогда для определения перемещений ротора, связанных с его прогибами, можно воспользоваться теорией изгиба балок. Таким образом, параметры ротора - распределенная масса m(x), распределенные экваториальный массовый момент инерции i(x) и полярный массовый момент инерции i0(x), изгибная жесткость EJ(x) - будут функциями одной переменной - продольной координаты сечения ротора.

Для ротора, свободного от опор и внешних нагрузок, линия, проходящая через центры тяжести площади поперечных сечений, представляет собой ось жесткости ротора, которую будем считать прямолинейной. Линия, проходящая через центры тяжести масс поперечных сечений, определяет ось инерции ротора. Неуравновешенность ротора определяется как отклонение в каждом сечении оси инерции от оси жесткости. На Рис. 14.5.5_2 показано положение осей жесткости и инерции в поперечном сечении недеформированного ротора в произвольном поперечном сечении. Начало Î1 системы координат O1xyz лежит на оси жесткости ротора, ось O1x направлена перпендикулярно плоскости чертежа и совпадает с осью жесткости. 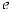Положение центра инерции характеризуется эксцентриситетом массы в рассматриваемом се- чении. Аналогично вводится перекос главной оси инерции Ã(x) = {γ1, γ2}.

Деформированное состояние в каждом сече- нии определяется параметрами [14.8.5], включа-

1075

Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.5_2

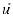
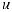
ющими вектор перемещения и вектор угла поворота поперечного сечения . Положение центра инерции при этом задается вектором . При деформациях ротора в каждом сечении возникают усилия, õарактеризующиеся вектором попереч-

íîé ñèëû		и вектором изгибаю-
щего момента		. Поперечное

сечение деформированного ротора показано на Рис. 14.5.5_3.

Здесь ось Ox неподвижной системы координат Oxyz совпадает с исходным положением оси жесткости недеформированного ротора. Система координат Oξηζ вращается вместе с ротором вокруг оси Oξ, совпадающей с осью Ox неподвижной системы Oxyz. Положение осей Oξηζ относительно неподвижной системы координат определяется углом ϕx=ϕξ=ωt поворота ротора вокруг оси Ox Oξ. Положение оси жесткости деформированного ротора задается точкой O1. Подвижная система координат O1ξ’η’ζ ’ жестко связана с ротором и вращается вместе с ним. Ее начало O1 лежит на оси жесткости деформированного ротора, а направление оси O1ξ’ совпадает с направлением касательной к оси жесткости деформированного ротора. Положение системы O1ξ’η’ζ’ относительно неподвижной системы Oxyz задается векторами

è		и углом ϕx=ϕξ=ωt .
		Точка O0 представляет собой положение оси

инерции деформированного ротора. Ее положение задается вектором , который, при прецессии по круговой орбите определяется выражением:

Рисунок 14.5.5_3

.(14.5.5-1)

Ориентация оси инерции находится из аналогичного выражения

	.(14.5.5-2)
Если неуравновешенность	лежит в од-

ной плоскости, а угловая неуравновешенность Ã(õ) отсутствует, то начальное угловое положение ротора можно выбрать таким образом, чтобы вектор был направлен вдоль оси Oη. Тогда

(14.5.5-3)

Составим уравнения колебаний ротора без учета гироскопического эффекта [14.8.26]. На Рис. 14.5.5_4 показан малый элемент dx ротора, а также внутренние и внешние силы, действующие на него. Условия динамического равновесия сил, действующих в направлениях осе Oy è Oz, имеют вид:

1076

Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.5_4

, (14.5.5-4)

а условия равенства моментов дает:

. (14.5.5-5)

Выражая перерезывающие силы их этих равенств:

(14.5.5-6)

И подставляя результат в (14.5.5-4), получим:

. (14.5.5-7)

Из теории изгиба балок имеем соотношения:

.(14.5.5-8)

Подставляя эти выражения в (14.5.5-7), нахо-

äèì:

,(14.5.5-9)

что, с учетом выражений (14.5.5-1), окончательно дает:

.(14.5.5-10)

Это уравнения колебаний ротора с распределенными параметрами без учета гироскопического эффекта. Система уравнений (14.5.5-10) содержит два уравнения четвертого порядка и для их решения требуется восемь граничных условий на концах ротора. Если имеющиеся на концах ротора опоры, демпферы, массы отнести к внутренним участкам, то концы ротора будут свободны от сил:

Qy(x = 0) = Qz(x = 0) = 0, My(x = 0) = Mz(x = 0)=0

на левом краю ротора и Qy(x = l) = Qz(x = l) = 0, My(x = l) = Mz(x = l) = 0 - на правом краю.

Возможны также и другие варианты гранич- ных условий, включающие значения перемещений или углов поворота в крайних сечениях. Однако, в любом случае их будет восемь.

Если внутри интервала x (0, l) между концами ротора в некоторых сечениях встречаются опоры, обладающие жесткостью и демпфированием, то реакции в опорах можно ввести в уравнения

1077

Глава 14 - Динамика и прочность ГТД

(14.5.5-10) с помощью функции c(x), характеризующей жесткость опор, и функции k(x), характеризующей коэффициенты сопротивления демпферов в опорах [14.8.5]:

.(14.5.5-11)

Функции c(x) è k(x) äëÿ âñåõ x (0, l) равны нулю, за исключением тех сечений, в которых расположены опоры. В этих сечениях функции принимают значения соответствующих параметров опор.

Для учета гироскопического эффекта обратим внимание на то, что элемент dx ротора (см. Рис. 14.5.5_4) можно рассматривать как тонкий диск толщиной dx, и для него справедливы соотношения (14.5.3-8) из раздела 14.5.3. Учитывая, что для тонких дисков между моментом инерции i0dx относительно оси вращения и моментом инерции idx относительно диаметра выполняется соотношение i0dx = 2i0dx, запишем эти соотношение в виде

.(14.5.5-12)

Внешние моменты my è mz в данном случае определяются выражениями (см. Рис. 14.5.5_4):

подстановка которых в (14.5.5-12) с учетом зависимостей (14.5.5-8) дает:

.(14.5.5-14)

Отсюда можно найти перерезывающие силы:

.(14.5.5-15)

и, подставив их в (14.5.5-4), получить:

Рисунок 14.5.5_5 - Ротор с равномерно распределенной массой

, (14.5.5-13)

1078

Глава 14 - Динамика и прочность ГТД

(14.5.5-16)

Уравнения (14.5.5-16) описывают вынужденные изгибные колебания, возбуждаемые неуравновешенностью ротора с переменными по длине массой и изгибной жесткостью при учете инерции поворота сечений и распределенного гироскопи- ческого эффекта. Так же как и в системе уравнений (14.5.5-10) здесь требуется восемь граничных условий аналогичного вида. Подобно уравнениям (14.5.5-11) можно ввести реакции опор в виде функций c(x) è k(x):

возбуждающих сил от неуравновешенности ротора. Уравнения (14.5.5-9) в этом случае примут вид:

, (14.5.5-18)

Поскольку первое уравнение от второго отли- чается только обозначениями, будем решать уравнение:

, (14.5.5-19)

которое описывает плоские колебания однородного стержня. Представим решение в виде произведения двух функций, одна из которых зависит только от времени t, а другая - только от продольной координаты x ротора:

u(x, t) = U(x) T(t).

(14.5.5-20)

Подставим (14.5.5-20) в (14.5.5-19):

.(14.5.5-21)

Разделим уравнение (14.5.5-21) на произведение U(x)·T(t) и перенесем один из членов в правую часть. Тогда получим:

.

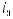
(14.5.5-17)

Рассмотрим частный случай - ротор постоянного сечения, свободно опертый по концам на абсолютно жесткие опоры (см. Рис. 14.5.5_5). Анализ свободных колебаний выполняется в отсутствие

. (14.5.5-22)

Произошло разделение переменных - в левой части равенства имеем функцию, зависящую только от x, а в правой - только от t. Равенство таких функций при любых значениях x è t возможно лишь в случае, если левая и правая части равны одной и той же постоянной величине, которую обозначим символом Ω2 .

Тогда приходим к двум обыкновенным дифференциальным уравнениям:

1079

Глава 14 - Динамика и прочность ГТД

. (14.5.5-23)

Поскольку решения линейных однородных дифференциальных уравнений известны, запишем решение:

(14.5.5-24)

Для отыскания постоянных D1,D2,D3,D4 необходимо задать граничные условия по концам ротора. Граничные условия, выраженные через D1,D2,D3,D4, представляют однородную систему четырех линейных алгебраических уравнений относительно D1,D2,D3,D4. Ненулевое решение такой системы существует только тогда, когда определитель системы равен нулю. Уравнение, получаемое в результате приравнивания нулю определителя системы уравнений для D1,D2,D3,D4, представляет трансцендентное уравнение относительно r. Из этого уравнения находим корни (бесконечное число корней), каждому из которых соответствуют свои частота и форма свободных колебаний ротора.

Общее решение уравнения (14.5.5-19) представляет бесконечную комбинацию

(14.5.5-25)

Учитывая структуру функции u(x, t), для жестких опор на концах ротора получим

.(14.5.5-26)

В развернутой форме эти уравнения при x=0 имеют вид:

D2n + D4n = 0,

(14.5.5-27)

-D2nr + D4nr2 = 0,

откуда получаем

D2n = D4n = 0 .

(14.5.5-28)

Ñучетом (14.5.5-26) граничные условия при

x= l имеют вид:

(14.5.5-29)

Условие ненулевого решения этих уравнений запишется в виде

(14.5.5-30)

èëè

2sin(rnl) sh(rnl) = 0.

(14.5.5-31)

Поскольку функция sh(rnl) равна нулю только при rn = 0 и при этом получается Ω = 0, то получа- ем условие (14.5.5-31) в форме:

1080

Глава 14 - Динамика и прочность ГТД

.

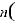
При этом для выполнения условий (14.5.5-29) необходимо выполнение равенства D3n=0. Таким образом, единственной отличной от нуля постоянной интегрирования, является D1n. Èòàê:

.

Собственные частоты колебаний находятся по формуле:

.(14.5.5-32)

Собственные формы колебаний выражаются функциями:

. (14.5.5-33)

Решение уравнения (14.5.5-19) приобретает

âèä:

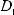
.(14.5.5-34)

Таким образом, ротор с распределенными параметрами имеет бесконечный спектр собственных частот и соответствующих форм собственных колебаний. В частном случае свободного опирания по концам ротора постоянного сечения с равномерно распределенной массой спектр собственных частот определяется соотношением (14.5.5-32), а соответствующие собственные формы - соотношением (14.5.5-33).

Собственные формы систем с распределенными параметрами обладают свойством ортогональности, которое выражается в виде соотношения:

. (14.5.5-35)

(14.5.5-10) или (14.5.5-17) путем приравнивания нулю правой части и отбрасывания членов, содержащих силы демпфирования в опорах (функции k(x)). Аналитическое решение получающихся уравнений в общем случае не возможно и ищется приближенное решение. Для этого аналогично соотношениям (14.5.5-20) - (14.5.5-23) выполняется разделение переменных, в результате которого уравнение относительно функции времени T(t) можно решить аналитически, а второе уравнение относительно функции U(x), описывающей форму собственных колебаний, решается путем численного интегрирования или другим приближенным методом.

Для организации процесса численного интегрирования и нахождения форм собственных колебаний требуется определение собственных частот, которые заранее не известны. Поэтому поступают следующим образом. В исследуемом частотном диапазоне задается ряд пробных значений частоты колебаний и последовательно для каждого значе- ния частоты выполняется интегрирование уравнения каким-либо численным методом (например, методом Рунге-Кутты). При этом из граничных условий типа (14.5.5-26) составляется система уравнений для определения произвольных постоянных, аналогичная (14.5.5-27), (14.5.5-29), и вы- числяется ее определитель. Поскольку расчет выполнен не для собственной частоты колебаний Ωn, оказывается, что этот определитель не равен нулю. Путем повторения расчетов для выбранных значе- ний частоты определяется интервал частот, внутри которого определитель изменяет знак (см. Рис. 14.5.5_6). Значение частоты, при котором определитель принимает нулевое значение, затем

	Уравнения колебаний ротора с неравномерно	Рисунок 14.5.5_6
	распределенной массой получаются из системы

1081

Глава 14 - Динамика и прочность ГТД

уточняется, например, методом «деления отрезка пополам». После определения с заданной точностью значения собственной частоты Ωn, находятся постоянные интегрирования и вычисляются соответствующая форма собственных колебаний Un(x). Для полученных таким образом форм колебаний с точ- ностью до погрешности вычислений также выполняется условие ортогональности (14.5.5-35).

Когда задача о свободных колебаниях уже решена и получен спектр собственных частот Ωn и собственных форм колебаний Un(x) в заданном частотном диапазоне, задачу о вынужденных колебаниях можно решить путем разложения в ряды по собственным формам. При этом предполагается, что распределенная неуравновешенность e(x) лежит в одной плоскости и решение уравнений (14.5.5-11) ищут в виде [14.8.5]:

(14.5.5-36)

Подстановка соотношений (14.5.5-36) в уравнения (14.5.5-11) и учет свойства ортогональности собственных форм Un(x)(14.5.5-35) позволяет получить ряд систем обыкновенных дифференциальных уравнений

,(14.5.5-37)

где обозначено

.(14.5.5-38)

Система (14.5.5-37) аналогична системе уравнений (14.5.2-5) для колебаний одномассового ротора, вследствие чего ее решения аналогичны решениям (14.5.2-10) системы (14.5.2-5). Амплитуды вынужденных колебаний определяются выражением:

.(14.5.5-39)

Проанализируем уравнения (14.5.5-37), соотношения (14.5.5-38) и решение (14.5.5-39). Можно отметить, что исходная неуравновешенность e(x) разлагается колебательной системой в ряды по собственным формам. При этом каждая форма резонирует независимо от других при совпадении ча- стоты вращения ротора с соответствующей собственной частотой (т.е. при соответствующей критической частоте вращения ωêð = Ωn). Интенсивность колебаний вблизи ωêð = Ωn определяется не всей неуравновешенностью e(x) ротора, а коэффициентом En ее разложения по собственным формам (14.5.5-38). Величину En можно интерпретировать как проекцию неуравновешенности e(x)на собственную форму Un(x).

Если неуравновешенность ортогональна собственной форме:

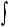
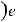
, (14.5.5-40)

то эта форма возбуждаться не будет, даже если ротор имеет относительно большую неуравновешенность.

На Рис. 14.5.5_7 показаны некоторые варианты неуравновешенности ротора и их влияние на возбуждение колебаний по различным формам. Так, неуравновешенности, показанные на Рис. 14.5.5_7а

è14.5.5_7б ортогональны второй форме колебаний,

èуровень колебаний здесь будет очень низким (теоретически равным нулю). Колебания по первой

èтретьей формам при этом будут существенными. На Рис. 14.5.5_7в неуравновешенность ортогональна первой и третьей формам, и ротор откликнется на возбуждение только по второй форме. На Рис. 14.5.5_7г неуравновешенность вызовет колебания по всем трем низшим формам колебаний.

Уровень колебаний на различных критических частотах определяется не только величиной

èраспределением неуравновешенности, но также

èдемпфированием колебаний. Опора ротора с од-

1082

Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.5_7 - Возбуждение колебаний ротора с распределенными параметрами в зависимости от распределения неуравновешенности

1083