Глава 14 - Динамика и прочность ГТД

14.5 - Динамика роторов. Вибрация ГТД

14.5.1 - Критическая частота вращения ротора. История вопроса

При эксплуатации машин с быстровращающимися роторами было замечено, что при определенной частоте вращения ротора может возникать повышенная вибрация и усиление общей тряски машины с последующим выходом ее из строя. Первые описания этого явления, названного критической частотой вращения ротора, относятся ко второй половине XIX века. На ранних этапах исследований были разработаны относительно простые математические модели, объясняющие основные особенности поведения ротора на критической частоте вращения. Уровень сложности моделей соответствовал развитию техники. Роторы машин того

Рисунок 14.5.1_1 - Модель одномассового ротора

времени, как правило, представляли собой вал на жестких опорах, в межопорном пролете которого была расположена масса в виде диска. Колебания такого ротора достаточно точно описывались в рамках модели одномассовой системы.

Рассмотрим простейшее и исторически первое объяснение критического режима вращения ротора. На Рис. 14.5.1_1 приведена схема ротора, представляющего собой невесомый вал в жестких опорах с диском посередине пролета. Ротор вращается с круговой частотой ω. Диск прикреплен к валу в своем геометрическом центре Î1. Массу диска M будем считать сосредоточенной в центре масс Î0, который в силу неточности балансировки не совпадает с Î1. Примем, что точка Î0 лежит в плоскости изогнутой линии вала и находится на расстоянии эксцентриситета e îò Î1. Таким образом, считаем, что центр масс вращается с круговой частотой ω по окружности радиуса y+e. Такое движение ротора называется прямой синхронной прецессией; как будет показано ниже, при отсутствии внешних переменных нагрузок в роторе рассматриваемой схемы реализуется именно такое движение.

На диск действует сила упругости вала и центробежная сила массы диска; другими силами пренебрегаем. Сила упругости, приложенная в точке Î1, пропорциональна прогибу вала y в точке крепления диска и направлена противоположно прогибу. Используем коэффициент упругой податливости вала α, который определяется как прогиб вала в точке крепления диска под действием единичной силы, приложенной в этой точке. Коэффициент α рассчитывается методами сопротивления материалов. Иногда используется обратный ему коэффициент жесткости c=1/α, определяемый как сила, приложенная в точке крепления диска, необходимая для создания единичного прогиба в этой точ- ке. В частности, в случае, когда диск расположен по середине между опорами вала постоянного се- чения: α = l3/48EJ, ãäå E - модуль упругости материала, J - момент инерции поперечного сечения вала. Используя податливость силу упругости можно записать как - y/α .

Центробежная сила пропорциональна радиусу окружности y+e, по которой движется центр масс, и определяется как Mω2(y+e). Равновесие этих сил при постоянной частоте вращения дает уравнение:

Mω2(y+e) -y/α = 0

(14.5.1-1)

Отсюда для прогиба вала получаем:

1061

Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.1-2 - Зависимость погиба вала от частоты вращения

(14.5.1-2)

Зависимость прогиба от частоты вращения ротора ω показана на Рис. 14.5.1_2. С возрастанием ω прогиб вала постепенно увеличивается. Критический режим, выражающийся в значительном увеличении прогиба вала, наступает при равенстве нулю знаменателя в (14.5.1-2); это происходит при частоте вращения:

(14.5.1-3)

Рассмотренный выше простейший анализ позволил в свое время понять основные закономерности динамики роторов:

-Возникло понимание того, что движение ротора на критической частоте вращения обусловлено неуравновешенностью ротора и связано со значительным изгибом вала (отсюда часто используемый термин «потеря динамической жесткости»).

-Стала понятной необходимость балансировки ротора для снижения вибраций на критических режимах. Из (14.5.1-2) видно, что при прочих рав-

ных условиях прогиб вала пропорционален вели- чине эксцентриситета e.

-Сложилось представление о необходимости повышения изгибной жесткости ротора так, чтобы критическая частота вращения располагалась выше рабочего диапазона частот вращения. Такие роторы принято называть жесткими.

-Было обнаружено и явление самоцентрирования ротора на закритических режимах работы. Из Рис. 14.5.1_2 видно, что при прохождении критической частоты вращения знак прогиба y меняется на отрицательный. Это означает, что направление прогиба и эксцентриситета становятся противоположными. При дальнейшем увеличении частоты вращения прогиб вала приближается по абсолютной величине к эксцентриситету, т.е. центр масс стремится к оси вращения; это и называется самоцентрированием.

По мере возрастания удельной мощности машин повышались и рабочие частоты вращения роторов. Проектирование жестких роторов становилось все более проблематичным, а иногда оказывалось невозможным. Это стимулировало исследования возможности работы роторов на режимах, превышающих критическую частоту вращения. Такие роторы называют гибкими. В 20...40-х годах XX века была разработана теория движения ротора в закритической области, установлена роль сил внутреннего трения, вызывающих неустойчивость ротора, и сил внешнего трения, способствующих демпфированию колебаний. Примерно тогда же было выяснено, что если искусственно понизить критическую частоту вращения, установив ротор на менее жесткие, упругие опоры, то попадание критической частоты в рабочий диапазон режимов в ряде случаев перестает быть опасным. На более низкой критической частоте вращения возникают меньшей величины неуравновешенные силы в роторе, что приводит меньшей динамической нагруженности машины. При работе на такой критической частоте вращения ротор ведет себя как относительно жесткое тело, вал изгибается незна- чительно, наибольшие колебательные перемещения реализуются в упругих опорах, что при необходимости может быть использовано для установки демпферов в опорах ротора для дополнительного снижения уровня колебаний. Соответствующее развитие критериев проектирования выразилось

âтом, что критическая частота вращения ротора перестала восприниматься инженерами как фатальное явление - сложилось представление об опасных и допустимых критических частотах. К опасным критическим частотам вращения стали относить только такие, на которых возникают зна-

1062

Глава 14 - Динамика и прочность ГТД

чительные изгибные деформации вала ротора, перемещения вала в опорных сечениях малы в сравнении с прогибом вала, на силовую конструкцию корпуса машины передаются значительные динамические усилия. Именно от таких критических частот в первую очередь старались освободить рабочий диапазон машины.

Многочисленные сопоставления результатов расчетов с данными наблюдений привели к уточ- нению модели. В расчетах стали учитывать гироскопический эффект диска, возникающий вследствие пространственного изменения направления оси вращения диска при изгибе вала. В теории сопротивления материалов были разработаны более совершенные модели изгиба стержней, позволившие повысить точность расчета жесткости вала.

Âнекоторых случаях при расчетах колебаний ротора учитывалась изгибная податливость диска и податливость элементов крепления диска к валу.

Âцелом расчеты критических частот вращения стали точнее.

Дальнейшее развитие газотурбинной и особенно авиационной техники, требовавшее существенного облегчения конструкции, привело к созданию роторов, к которым уже была неприменима модель в виде невесомого вала, несущего один или несколько дисков. Массы дисков компрессора и турбины стали сравнимы с массой вала ротора, появились конструкции роторов, в которых отдельные элементы выполняют функции вала и диска одновременно. Для анализа колебаний таких конструкций разработанные ранее модели и критерии проектирования были обобщены на случай систем с распределенными параметрами. Явления, происходящие при колебаниях роторов, усложнились - роторы с распределенными параметрами обладают целым спектром критических частот вращения.

Âавиационных двигателях, в отличие от подавляющего большинства газотурбинных установок наземного применения, колебания носят еще более сложный характер: сравнимость массовых и жесткостных параметров роторов и корпусов двигателя заставляет рассматривать их совместные колебания, т.е. колебания силовой схемы двигателя в целом. Наличие в двигателе двух или трех роторов, вращающихся с различными частотами, вызывает одновременное возбуждение колебаний на соответствующих частотах, каждый ротор при этом совершает движение, соответствующее синхронной и несинхронной прецессии. Эти особенности колебаний потребовали дальнейшего развития критериев проектирования и расчетных методов. Теперь требование отстройки всех критических частот вращения роторов за рабочий диапазон

режимов становится в принципе невыполнимым. В такой сложной колебательной системе, как силовая схема двигателя, спектр критических частот оказывается достаточно плотным - соответствующие критические режимы располагаются в среднем с интервалом 8...12 % от максимальной частоты вращения ротора и, таким образом, рабочие режимы двигателя практически всегда находятся в окрестности того или иного резонанса. В этой ситуации приобретают особую важность критерии оценки опасности или допустимости конкретной критической частоты вращения.

14.5.2 - Динамика одномассового ротора. Поступательные перемещения

Ниже будет показано, что критический режим вращения ротора представляет собой специфический вид вынужденных резонансных колебаний. Такое представление объясняет многие закономерности поведения роторов на критических режимах.

Рассмотрим снова простейшую модель (см. Рис. 14.5.1_1), представляющую симметричный относительно своей срединной плоскости диск массы M, закрепленный с эксцентриситетом в середине упругого невесомого вала, вращающегося с частотой ω. Вал считаем изотропным, т.е. его жесткость одинакова во всех направлениях, перпендикулярных оси вращения; будем также считать, что диск прикреплен к валу без перекосов, т.е. его срединная плоскость перпендикулярна оси вращения. В такой системе при изгибе вала диск будет совершать плоское движение, когда касательная к изогнутой оси вала в точке крепления диска остается параллельной оси подшипников ÎÎ’.

Рассмотрим сечение системы плоскостью, перпендикулярной оси подшипников ÎÎ’ и проходящей через точку Î1 крепления диска (эта плоскость совпадает со срединной плоскостью диска). Сечение показано на Рис. 14.5.2_1, где Î - точка пересечения плоскости диска с осью подшипников; Î1 - точка пересечения изогнутой оси вала с плоскостью диска; Î0 - центр масс диска; - радиус-вектор, характеризующий прогиб вала; - радиус-вектор, характеризующий положение центра масс диска; 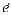- вектор эксцентриситета диска. Движение диска описывается тремя величинами: двумя декартовыми координатами центра масс диска и углом поворота диска ϕ - углом между осью Oy и вектором [14.8.5, 18.8.21]. В отличие от рассмотренной в предыдущем разделе модели здесь не вводится допущение о том, что точки Î1, Î1 è Î0 лежат на одной линии.

1063

Глава 14 - Динамика и прочность ГТД

Рисунок 14.5.2_1 - Плоскость вращения диска

Условие постоянства частоты вращения вала ω = const позволяет задать угловое положение диска выражением ϕ = ω t.

На диск действуют сила упругости вала, приложенная в точке Î1, и сила сопротивления, которые будем считать приведенными к той же точке Î1, а также сила инерции массы диска, приложенная в центре масс Î0.

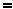
Сила упругости вала пропорциональна прогибу вала, т.е. определяется положением точки Î1 и равна , ãäå c - коэффициент жесткости системы, α - податливость. Знак минус показывает, что сила направлена против перемещения.

Если считать опоры вала абсолютно жесткими, то перемещение точки Î1 будет определяться только изгибом вала. В этом случае коэффициент жесткости c равен коэффициенту жесткости вала CÂ=1/α Â. Если же считать вал абсолютно жестким, а опоры податливыми, то перемещение точки Î1 будет определяться только деформациями опор, коэффициент жесткости c примет значение ñ = 2Ñ0, а податливость α = 1/c = α0 / 2, ãäå Ñ0, - жесткость каждой из опор, α0 = 1/ Ñ0, - податливость. В том случае, когда и вал и опоры не являются абсолютно жесткими, суммарную податливость системы можно определить как сумму податливостей:

α = α Â + α0/2,	(14.5.2-1)
откуда коэффициент жесткости:
ñ = 2Ñ0CÂ/(2C0 + CÂ).	(14.5.2-2)

Обозначим проекции радиуса-вектора прогибаоси координат uy è uz. Сила упругости вала тоже может быть представлена через проекции (-cuy) è (-cuz). Здесь принято, что жесткость системы одинакова во всех направлениях (изотропна).

Положение центра масс диска Î0 определяется радиусом-вектором , проекции которого на оси координат обозначим uy0 è uz0. Он является суммой вектора прогиба 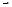и эксцентриситета (см. Рис.14.5.2_1). Положение последнего изменяется во времени в связи с вращением диска, а его проекции на оси координат равны esinωt è ecosωt. Координаты центра масс диска опреде-

ляются как сумма:

(14.5.2-3)

Помимо сил упругости на ротор действуют силы сопротивления. Будем считать их пропорциональными скорости точки Î1; введем коэффициент сопротивления K. Проекции силы сопротивления на оси координат равны è (они также как и силы упругости направлены против смещения.

Дифференциальные уравнения движения диска записываются через второй закон Ньютона в виде:

(14.5.2-4)

Продифференцируем (14.5.2-3) по времени и подставим в (14.5.2-4). После выполнения преобразований получим:

(14.5.2-5)

Уравнения (14.5.2-5), вообще говоря, не являются системой - они независимы. Каждое из них представляет собой уравнение вынужденных колебаний одномассовой системы, подобное уравнению (14.1.18-1). Собственная частота колебаний без учета сил сопротивления определяется как

. (14.5.2-6)

1064

Глава 14 - Динамика и прочность ГТД

Сначала рассмотрим случай, когда демпфирование отсутствует (K = 0); решение (14.5.2-5) ищем в виде:

(14.5.2-7)

подставляя в (14.5.2-5) находим

;

;(14.5.2-10)

(14.5.2-8)

Это решение совпадает с полученным выше на основе более простой модели решением (14.5.1-2).

Из (14.5.2-6) видно, что движение ротора представляет собой результат сложения изгибных гармонических колебаний в двух взаимно перпендикулярных плоскостях xoy è xoz с частотой, равной частоте вращения ротора. Критическая частота, при которой знаменатель (14.5.2-7) становится равным нулю, а амплитуда A стремится к бесконечности, равна собственной частоте изгибных колебаний системы:

ωêð = p.

(14.5.2-9)

Это позволяет интерпретировать критический режим как вынужденные резонансные колебания. Роль гармонической вынуждающей силы играет сила инерции неуравновешенных масс ротора.

Представление о движении ротора, как об упругих колебаниях позволяет использовать известные в теории колебаний подходы для объяснения и описания закономерностей критических режимов вращения. Так, например, множественность крити- ческих режимов реальных роторов, представляющих собой систему с бесконечным числом степеней свободы, объясняется наличием бесконечного спектра собственных частот и форм колебаний таких систем.

Рассмотрим теперь влияние демпфирования на критический режим. Общее решение уравнений (14.5.2-5) состоит из слагаемых, выражающих затухающие свободные колебания с частотой p, и слагаемых, описывающих установившиеся вынужденные колебания с частотой ω. Достаточно быстрое затухание свободных колебаний позволяет для описания стационарного режима использовать только ча- стное решение уравнений (14.5.2-5). Это решение, как показано в теории колебаний, имеет вид:

;

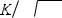
ãäå - логарифмический декремент колебаний.

Амплитуда колебаний центра масс Î0 с уче- том (14.5.2-3) выражается как:

(14.5.2-11)

Результаты расчетов по формулам (14.5.2-10) и (14.5.2-11) для величины δ = 0,1 представлены на Рис. 14.5.2_2. Видно, что в отличие от случая, когда демпфирование отсутствует, прогиб вала конечен даже на критическом режиме. Из (14.5.2-10)

Рисунок 14.5.2_2 - Зависимость амплитуды колебаний ротора от частоты вращения

1065