p1p2

3.1. Модель поведения потребителя: основные понятия и свойства

73

следует что v(p1, R1) > u(x), так как x — допустимое решение этой задачи. Тем более, должно выполняться и требуемое соотношение

u(x) = v(pα, Rα) 6 max{v(p1, R1), v(p2, R2)}.

(v) В предположении строгой выпуклости предпочтений непрерывность непрямой функции полезности следует из определения и непрерывности функции x(p, R), которую мы доказали в Теореме 2312.

Проиллюстрируем понятие непрямой функции полезности на примерах. Первый из них относится к гомотетичным предпочтениям.

Пример 12 (продолжение Примера 10):

Выше мы показали, что функция маршаллианского спроса при гомотетичности предпочтений (другими словами, при однородности функции полезности) однородна первой степени

по доходу, т. е. x(p, R) = Rx(p, 1). Таким образом, v(p, R)

= u(x(p, R)) = u(Rx(p, 1)) =

u(x(p, 1))R = a(p)R, где в качестве a(p) выступает u(x(p, 1)).

4

Пример 13 (продолжение Примера 11):

Непрямая функция полезности будет иметь вид:

v(p, R) = s

+ as

=

p1p2

+ a2(p1)2

(p2)2 + a2p1p2

Rp2

a2Rp1

= s

+ as

= s

rp1 + a2rp2 !

=

p1

(p2 + a2p1)

p2(p2 + a2p1)

p2 + a2p1

Rp2

a2Rp1

R

p2

p1

= s

1 ! = s

p2 +Ra2p1

p2√p1p2

R(p

2

+ a

p1).

+ a2p

2

Проверим выполнение свойств непрямой функции полезности, полученных нами в Теореме 24.

Возрастание непрямой функции полезности по доходу очевидно в силу возрастания функ-

√

ции x.

Убывание непрямой функции полезности по ценам следует из того факта, что функции 1

p1

r

и	a2 убывают по ценам и v(p, R) =	R	1	+ a2 .
			p1
	p2			p2
	Проверка квазивогнутости непрямой функции полезности достаточно громоздка, и мы ее
проводить не будем. Желающие могут проделать ее самостоятельно.					4

3.1.3Задача минимизации расходов и хиксианский спрос

Рассмотрим вопрос о том, какие денежные средства требуются потребителю при данных ценах на достижение заданного уровня благосостояния и какие потребительский наборы обеспечивают минимальное значение потребительских расходов. Ответы на эти вопросы можно получить с помощью следующей задачи:

ph → min

h X

h < x.

12Доказательство в общем случае читатель может найти в книге В. Гильденбранд: Ядро и равновесие в большой экономике, М.: Наука, 1986, с. 31.

3.1. Модель поведения потребителя: основные понятия и свойства

74

В этой задаче требование к минимально допустимому уровню благосостояния задается потребительским набором x. В верхнем лебеговском множестве набора x, L+(x) = { y X | y < x }, ищется самый дешевый (в ценах p) набор. На основе этой задачи приходим к понятию хиксианского спроса.

Определение 25:

Отображение

h(p, x) = argmin ph

h L+(x)

называется спросом по Хиксу (хиксианским спросом)13. В случае если данное отображение является однозначным, h(p, x) называется функцией спроса по Хиксу14.

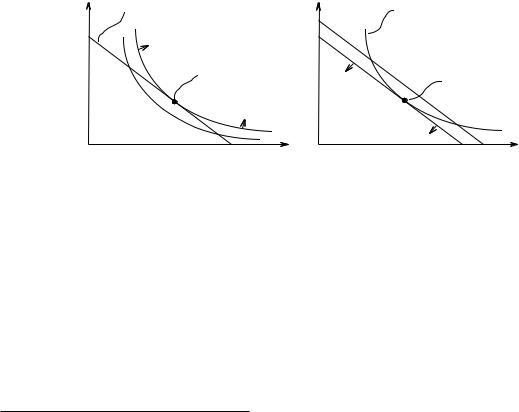
Таким образом, хиксианский спрос при заданных p и x — это самый дешевый потребительский набор при заданных ценах p, среди всех наборов, которые не хуже, чем x, в то время как обычный (маршаллианский) спрос — это наилучший с точки зрения предпочтений индивидуума набор в бюджетном множестве. На Рис. 3.2 в случае двух благ иллюстрируется разница в понятиях маршаллианского и хиксианского спросов.

x2 бюджетная прямая	h2	кривая безразличия
маршаллианский		хиксианский
спрос
		спрос
x1		h1

Рис. 3.2. Маршаллианский и хиксианский спрос

Если предпочтения представимы функцией полезности u : X → R, отображение хиксианского спроса может быть найдено как решение параметрического семейства задач математического программирования:

ph → min	(H)
h X
u(h) > u(x),

каждая из которых обычно называется двойственной (взаимной) к соответствующей задаче потребителя (задаче поиска маршаллианского спроса).

Следующая теорема устанавливает основные свойства отображения (функции) хиксианского спроса.

13Приведенное здесь определение хиксианского спроса не является классическим. В большинстве учебников хиксианский спрос определяется как набор, который дает заданный уровень полезности. Преимуществом данного здесь определения является то, что в нем не используются понятия и термины, ассоциирующиеся с кардиналистским подходом.

Наше изложение следует в русле ординалистского подхода к теории потребительского спроса, развитого Лайонелем Мак-Кензи (L. McKenzie: Demand Theory Without a Utility Index, Review of Economic Studies 24 (1957): 183–189). Поскольку исходными при ординалистcком подходе являются предпочтения, то желательно по возможности вводить такие понятия, которые не опираются непосредственно на функцию полезности.

14Понятие хиксианского спроса появилось, и получило свое развитие, в работах Джона Хикса (J. R. Hicks: Value and Capital, Oxford University Press, 1939, рус. пер. Дж. Р. Хикс: Стоимость и капитал, М.: Прогресс, 1993), Пола Самуэльсона (P. A. Samuelson: Foundations of Economic Analysis, Harvard University Press, 1947) и Лайонеля Мак-Кензи (см. сноску 13).

3.1. Модель поведения потребителя: основные понятия и свойства

75

Теорема 25 (свойства хиксианского спроса):

Пусть p Rl++ , предпочтения потребителя являются непрерывными. Тогда

(i)решение двойственной задачи потребителя существует, т. е. h(p, x) 6= x X ;

(ii)если предпочтения потребителя выпуклы, то h(p, x) — выпуклое множество;

(iii)если предпочтения потребителя строго выпуклы, то h(p, x) — непрерывная функция;

(iv)отображение h(p, x) однородно нулевой степени по p, т. е. h(λp, x) = h(p, x) (λ > 0);

(v)если x0 x00 , то h(p, x0) = h(p, x00);

(vi) для каждого h h(p, x) справедливо h x.

Доказательство: Доказательство в общих чертах идет по схеме доказательства Теоремы 23 и оставляется читателю в качестве упражнения.

Обсудим, как и в случае с маршаллианским спросом, необходимые и достаточные условия

оптимума задачи минимизации расходов (поиска хиксианского спроса)
min
ph → h	>	0	(H0)

u(h) > u(x),

Здесь предполагается, что X = Rl+ , т. е. h > 0 — условие того, что h — допустимый набор, и

что функция полезности u(·) определена на более широком, чем X = R+l			, открытом множестве
(например, Rl ), и является дифференцируемой.
Условия Куна — Таккера для задачи (H0) в точке hˆ имеют вид
ˆ	(2)	ˆ	ˆ
(1) − p + λru(h) 6 0;		(−p + λru(h))h = 0;
ˆ	(4)	λ > 0.
(3) λ(u(h) − u(x)) = 0;

Если набор ˆ , допустимый в задаче (H0), удовлетворяет этим условиям при некотором h

множителе Лагранжа λ, и функция полезности квазивогнута (предпочтения выпуклы), то

по обратной теореме Куна — Таккера ˆ является решением этой задачи. Действительно, по- h

скольку целевая функция ph линейна, то она вогнута; ограничение же задается квазивогнутой функцией u(h) − u(x).

С другой стороны, если ˆ — решение рассматриваемой задачи, то (при выполнении условий h

регулярности) найдется множитель Лагранжа , такой что для ˆ выполнены условия

λ (h, λ)

Куна — Таккера. Предположение r ˆ 6 обеспечивает выполнение условий регулярности u(h) = 0

в форме Куна — Таккера.

Таким образом, приведенные условия являются необходимыми и достаточными условиями

ˆ	ˆ
того, чтобы набор h	(h < x) являлся решением задачи минимизации расходов.
	ˆ	int X в более общей задаче (H) условия Куна — Таккера
Для внутреннего набора h
принимают более простой вид:
		ˆ
(1) − p + λru(h) 6 0;
	ˆ		(3) λ > 0.
(2) λ(u(h) − u(x)) = 0;

Заметим попутно, что, как несложно увидеть, если x = x(p, R) — решение задачи потребителя при ценах p Rl++ и доходе R > 0, и λ — множитель Лагранжа, отвечающий этому решению, такой что λ > 0, то множитель Лагранжа в соответствующей задаче поиска хиксианского спроса λ должен быть равен λ1 . (О взаимосвязи двух задач речь пойдет ниже в Теореме 27.)

Используя условия Куна — Таккера, найдем теперь функцию хиксианского спроса для случая, рассматривавшегося нами в Примере 11.

3.1. Модель поведения потребителя: основные понятия и свойства

76

Пример 14 (продолжение Примера 11):

Для функции полезности u(x) = √x1 + a√x2 хиксианский спрос является решением следующей задачи:

p1h1 + p2h2 → min

h>0

pp

h1 + a h2 > u(x).

Функция Лагранжа для этой задачи имеет вид:

p p

L(h, λ) = −p1h1 − p2h2 + λ( h1 + a h2 − u(x)).

Предположим, что решение является внутренним, т. е. h1 > 0, h2 > 0. При этом из условий

Куна — Таккера получим

−p1 + λ

1

= 0,

+ λa

1

= 0.

2√

−p2

2√

h1

h2

√

√

Несложно заметить, что из этих двух равенств следует λ > 0, а, значит,

h1

+ a h2 = u(x).

√

p1

p1

2

√

√

√

h2

Отсюда имеем

√

=

p2 или

h2 =

ap

h1 . Так как

h1 + a

h2

= u(x), то h1 +

2 p1

√

a h1

p2u(x)

2

2

ap1u(x) 2

a

p2

h1 = u(x) или h1 =

2

p1

, откуда, h2 =

2

p1

.

p2+a

p2+a

ограничению за-

Читатель может проверить,

что невнутренние наборы,

удовлетворяющие

дачи, дают более высокое значение расходов, чем найденный набор, т. е. найденный набор является оптимумом, причем единственным. (что, впрочем очевидно, так как решение задачи минимизации расходов при строго вогнутой функции полезности (строго выпуклых предпочтениях) единственно, а условия Куна-Таккера в данном случае являются не только необходимыми, но и достаточными. Таким образом, хиксианский спрос равен

	p2u(x)		2		ap1u(x)	2
h(p, x) =				,		.
	p2 + a2p1				p2 + a2p1

Проиллюстрируем теперь свойства функции хиксианского спроса, доказанные в Теореме 25. То, что хиксианский спрос однороден нулевой степени по ценам очевидно. Действительно,

tp2u(x)

2

atp1u(x)

2

h(tp, x) =

,

=

tp2 + a2tp1

tp2 + a2tp1

p2u(x)

2

ap1u(x)

2

=

,

= t0h(p, x).

p2 + a2p1

p2 + a2p1

Проверим, что u(h(p, x)) = u(x). Подставив хиксианский спрос в функцию полезности, мы получим:

qq

u(h(p, x)) = h1(p, x) + a h2(p, x) =

ss

	p2u(x)			ap1u(x)			p2u(x)		ap1u(x)
= (		)2	+ a (		)2	=		+ a		= u(x).	4
	p2 + a2p1			p2 + a2p1			p2 + a2p1		p2 + a2p1

Аналогом непрямой функции полезности в двойственной задаче потребителя является функция расходов15.

15Опять же, как и в случае с хиксианским спросом (см. сноску 13), мы здесь используем нетрадиционное определение функции расходов. Используемый нами вариант называется измеряемой в деньгах функцией полезности, /как по русски сказать??/.

3.1. Модель поведения потребителя: основные понятия и свойства

77

Определение 26:

Функция e(p, x) = ph, где h h(p, x) — хиксианский спрос при данных p и x, называется

функцией расходов (затрат).

Другими словами, функция расходов e(p, x) — значение целевой функции двойственной задачи в точке оптимума при данных p и x. Согласно определению, для каждого достижимого уровня полезности функция расходов указывает минимальный уровень расходов (дохода), обеспечивающий такой уровень полезности.

Теорема 26 (свойства функции расходов):

Пусть выполнены предположения Теоремы 25. Тогда

(i)функция e(p, x) однородна первой степени по ценам: e(λp, x) = λe(p, x) (λ > 0);

(ii)функция e(p, x) не убывает по ценам: e(p0, x) 6 e(p, x) при p > p0 ;

(iii)функция e(p, x) — вогнутая функция цен p;

(iv)функция e(p, x) непрерывна;

(v) x < y тогда и только тогда, когда e(p, x) > e(p, y);

Доказательство: (i) Первый пункт утверждения следует из того, что решения двойственной

задачи при векторе цен p и векторе цен λp совпадают.

ph = e(p, x). С другой

(ii) Пусть p0

>

p, p0 = p, h

h(p, x) и h0

h(p0, x). Тогда ph0

>

6

стороны, e(p0, x) = p0h0 > ph0 . (Заметим, что если h0

> 0, то e(p0, x) > e(p, x).)

(iii) Мы должны показать, что для двух произвольных векторов p1

и p2 при 0 6 α 6 1

1

2

1

2

˜

выполняется e(αp

+(1−α)p

, x) > αe(p

, x)+(1−α)e(p

, x). Пусть h — решение двойственной

задачи при ценах p

α

1

+(1−α)p

2

˜

α

, x). Отметим, p

α ˜

α

, x). Допустимое

= αp

, т. е. h h(p

h = e(p

множество { h X

h < x }

˜

не зависит от p, поэтому потребительский набор h допустим в

двойственной задаче как при ценах p1 , так и при ценах p2 . Из определения функции расходов

˜	1		1 ˜	2		2 ˜
и допустимости h имеем e(p		, x) 6 p h и e(p			, x) 6 p h. Отсюда
	1			2		, x) 6 p	α ˜	α	, x).
	αe(p		, x) + (1 − α)e(p				h = e(p

(iv) Доказательство непрерывности оставляем читателю в качестве упражнения. Заметим только, что непрерывность функции расходов по ценам следует из того, что она является вогнутой (как функция цен) и определена на открытом множестве (а любая вогнутая функция непрерывна во внутренности своей области определения).

(v ) Докажем, что из x < y следует e(p, x) > e(p, y). Так как x < y, то все потребительские наборы, допустимые в двойственной задаче при наборе параметров (p, x), являются допустимыми в этой задаче при наборе параметров (p, y). В том числе, допустимыми являются и наборы, принадлежащие h(p, x), а это и означает что e(p, x) > e(p, y).

(v ) Докажем, что из e(p, x) > e(p, y) следует x < y. Предположим противное, то есть

	˜
y x. При этом e(p, y) = e(p, x) и, значит, h(p, y) h(p, x). Возьмем h h(p, y). В силу
непрерывности предпочтений и того, что X — выпуклое множество и 0 X , существует
˜	˜
такое число α < 1, что αh < x. В этом случае p · (αh) = αe(p, y) < e(p, x), что противоречит
определению e(p, x).

На основании пункта (v) можно говорить о функции e(p, x), как о функции полезности, которая представляет исходные предпочтения. Это свойство — одно из самых важных свойств функции расходов и является ключевым при обсуждении вопроса о восстановлении предпочтений по наблюдаемой функции спроса (см. параграф 3.C).

Проиллюстрируем теперь нахождение функции расходов.

Пример 15 (продолжение Примера 11):

√

√ Найдем функцию расходов e(p, x), соответствующую функции полезности u(x) = x1 + a x2 . Как было показано выше, функция хиксианского спроса для рассматриваемого потре-

3.1. Модель поведения потребителя: основные понятия и свойства

78

бителя равна h(p, x) =

p2u(x)

2

ap1u(x)

2

,

. Из определения функции расходов имеем:

p2+a2p1

p2+a2p1

p2u(x)

2

ap1u(x)

2

e(p, x) = p1h1(p, x) + p2h2(p, x) = p1

+ p2

=

p2 + a2p1

p2 + a2p1

u(x)

2

u(x)

2

=

(p1(p2)2

+ a2p2(p1)2) =

(p1p2

+ a2p1)p1p2 =

p2 + a2p1

p2 + a2p1

=

u(x)

2

p1p2(u(x))2

(p1p2 + a2p1)p1p2 =

.

p2 + a2p1

p2 + a2p1

На примере данной функции проиллюстрируем выполнение свойств, доказанных в Теореме 26.

Покажем, что полученная функция однородна первой степени по ценам.

e(tp, x) =

tp1tp2(u(x))2

= t

p1p2(u(x))2

= te(p, x).

tp2 + a2tp1

p2 + a2p1

Проверим свойство неубывания по ценам. Отметим, что

p1p2(u(x))2

(u(x))2

e(p, x) =

=

.

p2 + a2p1

1

+ a2

p1

p2

Действительно при росте при росте p1 величина

1

убывает, что в свою очередь влечет рост

p1

2

значения дроби

(u(x))

, и, тем самым, рост функции расходов.

1 a2

+

p2

p1

Проверим теперь вогнутость функции расходов по ценам. Матрица вторых частных про-

изводных для функции расходов e(p, x) =						p1p2(u(x))2
									равна
						p2+a2p1
H =	2a2p1p2				(u(x))2			2a2p12		(u(x))2 .
		−		2a2p22	(u(x))2		2a2p1p2			(u(x))2
				(p2+a2p1)3				(p2+a2p1)3
			(p2+a2p1)3				− (p2+a2p1)3

Несложно заметить, что первый главный последовательный минор отрицателен, а второй равен 0. Значит, главные последовательные миноры чередуют свой знак, начиная с первого, который отрицателен. Таким образом, матрица H отрицательно полуопределена и, соответственно, функция e(p, x) вогнута.

Наконец проверим, что x < y e(p, x) > e(p, y). Действительно, в силу положительности

цен имеем: e(p, x) > e(p, y) p1p2(u(x))2 > p1p2(u(y))2 (u(x))2 > (u(y))2 . Так как u(x) =

p2+a2p1 p2+a2p1

√x1 +a√x2 и, тем самым, неотрицательна, то условие (u(x))2 > (u(y))2 эквивалентно условию

u(x) > u(y). То есть, e(p, x) > e(p, y) u(x) > u(y). Откуда по определению функции

полезности имеем, что e(p, x) > e(p, y) x < y.

4

Рассмотрим теперь вопрос о взаимосвязи прямой и двойственной задач потребителя. Следующая теорема, называемая теоремой взаимности (двойственности), устанавливает условия совпадения решений прямой и двойственной задач потребителя.

Теорема 27 (теорема взаимности /двойственности/):
Пусть X = R+l и p R++l	, а предпочтения потребителя непрерывны. Тогда
(i) если предпочтения локально ненасыщаемы, то x¯ x(p, R) влечёт x¯ h(p, x¯);
¯	¯	¯

(ii) для любого h h(p, x¯), где x¯ X , выполнено h x(p, e(p, x¯)) = x(p, ph).

3.1. Модель поведения потребителя: основные понятия и свойства

79

Доказательство: (i) Предположим противное. Пусть x¯ / h(p, x¯), т. е. в двойственной задаче существует потребительский набор h0 < x¯ такой, что px¯ > ph0 . Из локальной ненасыщаемости предпочтений следует, что существует набор h00 , такой что h00 h0 < x¯ , и при этом px¯ > ph00 .

А это противоречит оптимальности x¯ в прямой задаче потребителя.
¯	¯
(ii) Случай h = 0	очевиден, поэтому будем исходить из того, что h 6= 0 (и, следователь-
¯	¯	p	¯
но, ph > 0). Набор	h допустим в прямой задаче потребителя при ценах		и доходе ph.

Предположим, что он не является решением этой задачи. Тогда существует потребительский

набор ¯ ¯ такой, что 0 ¯ . В силу непрерывности предпочтений найдется x = ph B(p, ph)) x h

0 < α < 1 такое, что αx0 < h¯ . Набор αx0 стоит дешевле h¯	в ценах p, а это противоречит
¯
оптимальности h в двойственной задаче потребителя.

Следующая теорема является следствием предыдущей и устанавливает другие связи между характеристиками прямой и взаимной задачи потребителя.

Теорема 28 (соотношения двойственности, следствие Теоремы 27):

Пусть выполнены все предположения Теоремы 27 (включая локальную ненасыщаемость предпочтений). Тогда верны следующие тождества:

(i)для любого x¯ x(p, R) выполнено e(p, x¯) = R;

(ii)для любого x¯ x(p, R) выполнено x(p, R) = h(p, x¯);

(iii)v(p, e(p, x¯)) = u(x¯);

(iv) x(p, e(p, x¯)) = h(p, x¯).

Доказательство: (i) Теорема 27 показывает, что для любого x¯ x(p, R) выполнено x¯ h(p, x¯). Отсюда, по определению функции расходов, e(p, x¯) = px¯ . В силу локальной ненасыщаемости предпочтений px¯ = R.

(ii) То, что для любого x¯ x(p, R) выполнено x(p, R) = h(p, x¯), является тривиальным

следствием пунктов (i) и (iv).
¯	X . Согласно пункту (vi) Теоремы 25 при непре-
(iii) Пусть h h(p, x¯) при некотором x¯
	¯
рывности предпочтений должно выполняться u(h) = u(x¯). Кроме того, по доказанной теореме
¯	¯

двойственности h x(p, e(p, x¯)), т. е. набор h оптимален в прямой задаче при ценах p и дохо-

де ¯ . Таким образом, по определению непрямой функции полезности ¯ ¯ , e(p, x) v(p, e(p, x)) = u(h)

откуда v(p, e(p, x¯)) = u(x¯).

(iv) Включение h(p, x¯) x(p, e(p, x¯)) доказано в теореме двойственности. Докажем обратное включение. Пусть x x(p, e(p, x¯)). Из пункта (i) Теоремы 27 следует, что x h(p, x), а из пункта (i) доказываемой теоремы — что e(p, x) = e(p, x˜). Из пункта (v) Теоремы 26 следует, что x x¯ . Таким образом, h(p, x) = h(p, x¯), и поэтому x h(p, x¯).

Проиллюстрируем полезность установленных соотношений двойственности. Пусть, решив задачу потребителя, мы нашли функцию спроса и непрямую функцию полезности. Как демонстрируют следующие примеры, этой информации достаточно для того, чтобы найти функцию хиксианского спроса и функцию расходов, не решая соответствующую двойственную задачу.

Пример 16:

Как показано в Примерaх 11 и 13, функции полезности u(x) = √x1 + a√x2 соответствует маршаллианская функция спроса

x(p, R) = p1p2 + a2

(p1)2 ; (p2)2 + a2p1p2 ! .

Rp2

a2Rp1

и

e(p,x)(p2+a2p1)

q

p2p1

непрямая функция полезности v(p, R) =

R(p2+a2p1)

. Из соотношения v(p, e(p, x)) = u(x),

имеем q

= u(x). Отсюда несложно выразить расходы через полезность: e(p, x) =

p2p1