3.2. Дифференциальные свойства задачи потребителя

84

/110. Сформулируйте и докажите аналоги Теорем 23–27 для случая, когда доход потребителя формируется за счет продажи начальных запасов w.

/111. Сформулируйте и докажите аналоги Теорем 23–27 для случая, когда доход потребителя формируется за счет заработной платы. Почасовая ставка заработной платы равна w, потребитель располагает 24 часами времени в сутки. Время отдыха является одним из благ, количество потребления которого выбирает потребитель.

/112. [MWG] Рассмотрите функцию расходов следующего вида:

e(p, x) = exp k K αk ln(pk) +	k K pkβk u(x) .
X	Y

При каких ограничениях на параметры αk , βk данная функция является функцией расходов? С учетом ответа на первый вопрос найдите отвечающую ей непрямую функцию полезности.

/113. Пусть непрямая функция полезности имеет вид a(p) + b(p)R. Какими свойствами должны обладать функции a(p) и b(p) для того, чтобы данная функция была непрямой функцией полезности рационального потребителя.

/114. Функция полезности называется псевдовогнутой, если из условия ru(x)(y − x) 6 0, следует, что u(y) 6 u(x). Покажите, что если функция полезности является псевдовогнутой, то условия Куна — Таккера являются достаточными условиями для нахождения решения задачи потребителя. Покажите, что любая вогнутая функция является псевдовогнутой, а любая псевдовогнутая функция является квазивогнутой.

/ 115. Пусть функция полезности равна u(x) = (x1 + x2 −2)3 . Цена на первый товар равна 1, а на второй — 2. Доход потребителя равен 3. Проверьте, что целевая функция квазивогнута и локально ненасыщаема. Покажите, что точка (1, 1) удовлетворяет условиям Куна — Таккера,

но не является оптимальной.

/ 116. Пусть функция спроса некоторого потребителя равна x(p, R) =

αR ,

(1−α)R

, а непря-

мая функция полезности равна v(p, R) =

αα(1

−

α)(1−α)R

p1

p2

. Найдите функцию расходов и хикси-

анский спрос.

p1αp2(1−α)

/ 117. Покажите, что функция v(p, R) =

R

+

R

удовлетворяет всем свойствам непрямой

p1

p2

функции полезности и вычислите на ее основе функцию расходов и функции спроса (маршаллианского и хиксианского).

/118. Проверьте выполнение соотношений двойственности (взаимности) в случае, если поведение потребителя описывается функцией полезности: u(x) = [x1x2], где [·] - оператор взятия целой части.

/119. Пусть функция полезности потребителя аддитивно-сепарабельна, то есть имеет вид

в		P	l
			i=1 ui(xi). Запишите достаточные условия оптимальности для задачи потребителя
u(x) =
	предположении, что потребитель имеет выпуклые, локально ненасыщаемы предпочтения.
			i	→	+	∞	при xi	→	0, то потребитель покупает все блага в положи-
Покажите, что если u0(xi)
тельных количествах.
/ 120.		Пусть обобщенная функция полезности, представляющая некоторые нетранзитивные

предпочтения, имеет вид Δ(x, y) = y1−1/2x12/2 + ln(x3) − x−1 1/2y21/2 − ln(y3). Найдите маршаллианский спрос данного потребителя. (Для пояснения обозначений см. Теорему 21 на с. 59.)

3.2Дифференциальные свойства задачи потребителя

Вданном параграфе дополнительно предполагается, что функция спроса, непрямая функция полезности и функция расходов потребителя являются дифференцируемыми. (Условия,

∂h

∂pi

3.2. Дифференциальные свойства задачи потребителя

85

гарантирующие дифференцируемость этих функций, приведены в приложении ??). При выполнении условия дифференцируемости непрямой функции полезности, функции расходов и функций маршаллианского и хиксианского спросов выполняются три важных свойства теории потребителя: лемма Шепарда, тождество Роя и уравнение Слуцкого.

Связь между функциями расходов и (хиксианского) спроса описывается леммой Шепарда.

Теорема 29 (Лемма Шепарда16):

Пусть решение взаимной (двойственной) задачи внутреннее и выполнены условия Тео-

ремы 37, тогда17

∂e(p, x) = hi(p, x). ∂pi

Доказательство: Учитывая значение этого результата для теории потребления, укажем несколько его обоснований.

Первое доказательство. По определению функции расходов e(p, x) = ph(p, x) p, x. Продифференцировав это тождество по pi , получим соотношение:

	∂e(p, x)		l	∂hj(p, x)
		= hi(p, x) +	pj		.
	∂pi		jX	∂pi
			=1

Остается доказать, что второе слагаемое равно нулю.

Замечание: Данное свойство стоит проинтерпретировать. Хотя при изменении цен рассматриваемых благ потребитель меняет свое поведение, предпочитая, вообще говоря, другой потребительский набор, при расчете изменения расходов на приобретение нового набора в первом приближении можно не учитывать этого изменения спроса потребителя. Другими словами, новые расходы в первом приближении рассчитываются, как если бы оптимальный выбор остался неизменным, т. е. эти новые расходы равны стоимости старого набора в новых ценах. Изменение спроса проявляется лишь во втором приближении.

Докажем это. Пусть второе слагаемое не равно нулю, например, положительно, т. е. p

∂h

>

0

h

= h(p

εei, x)

ei

i

ε > 0

∂pi

. Рассмотрим наборы вида

ε

−

, где

—

-й орт,

. Согласно

пункту (vi)

∂h

Теоремы 25 из непрерывности предпочтений следует h(p, x) x и hε x. Из p

> 0

∂pi

следует, что при достаточно малом ε будет выполнено неравенство p(h(p, x) −hε) > 0. Но это неравенство противоречит тому, что h(p, x) минимизирует расходы. Невозможность p < 0

доказывается аналогично, с помощью введения наборов вида h(p + εei, x).

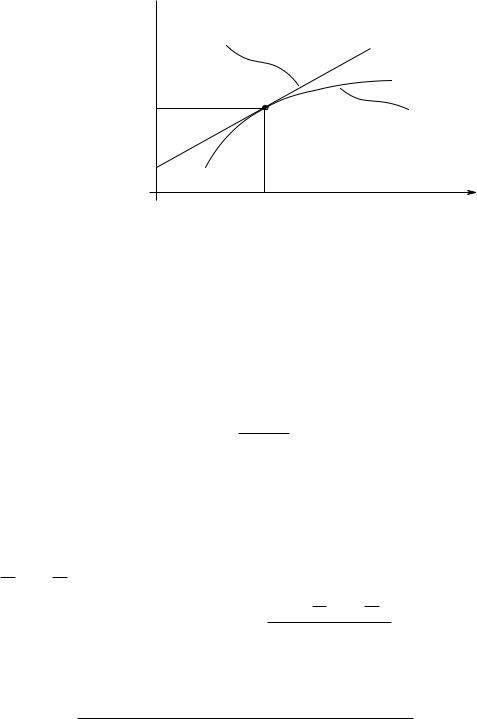
Второе доказательство. Идея другого доказательства этого факта заключается в постро-

ении касательной для графика функции расходов.

Обозначим p−i = (p1, . . . , pi−1, pi+1, . . . , pl), и p = (pi, p−i). Пусть p — некоторая точка. Зафиксируем все цены, кроме цены i-го блага p−i = p−i . Покажем, что прямая pihi(pi, p−i, x)+

P

6 p hj(pi, p , x) касается графика функции e(pi, p , x) в точке p . Действительно, набор

j=i j −i −i i

h(p , x) при ценах p требует минимальных расходов на приобретение из наборов, обеспечивающих тот же уровень благосостояния, что и потребительский набор x. При любых других ценах он допустим, но, вообще говоря, не минимизирует расходы. При ценах (pi, p−i) минимум расходов, необходимых для достижения того же уровня благосостояния, достигается на потребительской корзине h(pi, p−i, x). Другими словами, справедливо следующее неравенство:

e(pi, p−i, x) =
= p h (p , p , x) +				p h (p , p , x) p h (p , x) +				p h (p , x).
i i i	−	i	X6	j j i	−	i 6	i i	Xj6	j
								j
			j=i					=i

16R. W. Shephard: Theory of Cost and Production Functions, Princeton University Press, 1970.

17На самом деле, для справедливости данного утверждения достаточно дифференцируемости функции расходов и непрерывности предпочтений.

= hi(p, x).

3.2. Дифференциальные свойства задачи потребителя		86
При pi = p здесь выполнено равенство. Таким образом, максимум функции f(pi) = e(pi, p		, x)	−
i	−i
pihi(p , x) достигается в точке pi . Из необходимого условия максимума (f0(pi) = 0) следует
доказываемое соотношение.

e,R (расходы)

pihi(pi,p−i,x)+Pj6=ipj hj(pi,p−i,x)

A

e(p ,x)

e(pi,p−i,x)

pi

pi

Рис. 3.4. Иллюстрация доказательства леммы Шепарда

Второй способ доказательства иллюстрирует Рис. 3.4. Кривая e(pi, p−i, x) лежит под пря-

мой

pihi(pi, p−i, x) + X pj hj(pi, p−i, x)

j6=i

и имеет с ней общую точку (pi , e(p , x)) (точка A на рисунке). Значит, эта прямая является

касательной к кривой e(pi, p−i, x). Наклон прямой равен hi(p , x). Таким образом, производная функции e(pi, p−i, x) в точке pi равна hi(p , x):

∂e(p, x)

∂pi

Из леммы Шепарда следует, что по функции расходов всегда можно построить функцию (хиксианского) спроса. Отметим также, что из нее следует, что функции расходов является дважды непрерывно дифференцируемой, так как непрерывно дифференцируемым является хиксианский спрос.

Пример 18:

Выше (в Примере 15) мы нашли, что для потребителя с функцией полезности u(x) = √x1 + a√x2 функция расходов равна

e(p, x) = p1p2(√x1 + a√x2)2 . p2 + a2p1

Убедимся для данной функции расходов в выполнении леммы Шепарда для первого товара. Продифференцируем функцию расходов e(p, x) по p1 :

∂e(p, x)

=

p2(√

+ a√

)2(p2 + a2p1) − a2p1p2(√

+ a√

)2

x1

x2

x1

x2

=

∂p1

(p2 + a2p1)2

(√

+ a√

p2

)2

x1

x2

=

2

= h1(p, x).

(p2 + a2p1)2

Вполне естественно, что в качестве результата дифференцирования мы получили найден-

ный нами ранее в Примере 14 хиксианский спрос.

4

3.2. Дифференциальные свойства задачи потребителя

87

??он вообще по жизни француз Рене Руа :)

Теорема 30 (тождество Роя):

Пусть выполнены условия Теоремы 29, тогда

−	∂v∂pi	,	∂R	= xi(p, R)
	(p, R)		∂v(p, R)

Доказательство: Для доказательства этого тождества воспользуемся одним из тождеств взаимности:

v(p, e(p, x)) = u(x).

Продифференцируем это тождество по pi :

∂v(p, e(p, x))

+

∂v(p, e(p, U))

∂e(p, x)

= 0.

∂pi

∂R

∂pi

По лемме Шепарда

∂e(p,x)

= hi(p, x), следовательно

∂pi

∂v(p, e(p, x))

+

∂v(p, e(p, x))

hi(p, x) = 0.

∂pi

∂R

В качестве x возьмем x = x(p, R).

Воспользуемся тождествами h(p, x(p, R)) ≡ x(p, R) и e(p, x(p, R)) ≡ R. Из них следует,

что верно соотношение

−∂v∂pi

,

∂R

= xi(p, R).

(p, R)

∂v(p, R)

.

Пример 19:

Как показано ранее, для потребителя с функцией полезности u(x) = √

+ a√

непря-

x1

x2

∂v(p,R)

q

∂v(p2,R1)

мая функция полезности равна v(p, R) =

R(p2+a2p1)

. Проиллюстрируем тождество Роя для

p p

первого товара. Для этого найдем

и

:

∂R

∂p1

∂R

= 2s

2Rp2p1

1

)

∂v(p, R)

1 (p

+ a2p

и

∂v(p, R)

1

a2p1p2R − p2R(p2 + a2p1)

=

=

p2p1

∂p1

2sR(p2 + a2p1)

(p2p1)2

2s

R(p2 + a2p1)

(p1)2

=

1

p2p1

−R

.

С учетом этого

,

= s

(p1)2 ,s

−

∂pi

∂R

Rp2p1 1

)

= p1

(p2 + a2p1).

R(p2

+ a2p1)

∂v(p, R)

∂v(p, R)

p2p1

R

(p2 + a2p

Rp2

Как и ожидалось, найденная функция представляет собой спрос на первый товар для функции
полезности u(x) = √x1 + a√x2 .	4

3.2. Дифференциальные свойства задачи потребителя						88
Теорема 31 (уравнение Слуцкого18):
Пусть выполнены условия Теоремы 29, тогда
	∂hi(p, x(p, R))	=	∂xi(p, R)	+	∂xi(p, R)		xj(p, R).
	∂pj		∂pj			∂R

Доказательство: Для доказательства воспользуемся одним из тождеств взаимности: x(p, e(p, x¯)) = h(p, x¯). Продифференцируем это тождество по pj :

∂xi(p, e(p, x¯))	+	∂xi(p, e(p, x¯))		∂e(p, x¯)	=	∂hi(p, x¯)	.
∂pj		∂R		∂pj		∂pj

Воспользуемся леммой Шепарда ∂e(p,x) = hi(p, x). В качестве потребительского набора x

∂pi

возьмем x(p, R). При этом в силу соотношений взаимности имеем hj(p, x(p, R)) = xj(p, R) и e(p, x(p, R)) = R.

Следовательно,

	∂hi(p, x(p, R))	=	∂xi(p, R)	+	∂xi(p, R)	xj(p, R).
	∂pj		∂pj		∂R

Пример 20:

Проиллюстрируем уравнение Слуцкого для первого товара и второй цены для рассмотрен-

ной функции полезности u(x) =

√

+ a√

. Функция спроса для этой функции полезности

x1

x2

Rp2

a2Rp1

равна x(p, R) =

;

. Функция хиксианского спроса равна h1(p, x) =

p1p2+a2(p1)2

(p2)2+a2p1p2

p22(√

+a√

)2

∂x1(p,R)

∂x1(p,R)

∂h1(p,x(p,R))

x1

x2

. Найдем

,

x2(p, R) и

:

(p2+a2p1)2

∂p2

∂R

∂p2

∂x1(p, R)

=

R(p1p2 + a2(p1)2) − Rp1p2

=

∂p2

(p1p2 + a2(p1)2)2

a2R(p1)2

a2R

=

=

;

(p1)2(p2 + a2p1)2

(p2 + a2p1)2

∂x1(p, R)

x2(p, R) =

p2

·

a2Rp1

=

∂R

p1p2 + a2(p1)2

(p2)2 + a2p1p2

=

a2Rp1p2

=

a2R

;

p2p1(p2 + a2p1)2

(p2 + a2p1)2

∂h1(p, x)

=

2p2(p2 + a2p1)2 − 2(p2)2(p2 + a2p1)

(√

+ a√

)2 =

x1

x2

∂p2

(p2 + a2p1)4

=

2a2p1p2

(√

+ a√

)2;

x1

x2

(p2 + a2p1)3

∂h1(p, x(p, R))

=

2a2p1p2

(v(p, R))2

=

∂p2

(p2

+ a2p1)3

=

2a2p1p2

·

R(p2 + a2p1)

=

2a2R

.

(p2 + a2p1)3

p2p1

(p2 + a2p1)2

18E. Slutsky: Sulla teoria del bilancio del consumatore, Giornali degli economisti e rivista di statistica 51 (1915): 1–26, рус. пер. Е. Е. Слуцкий: К теории сбалансированного бюджета потребителя, в кн. Народнохозяйственные модели. Теоретические вопросы потребления, М.: Изд-во АН СССР, 1963

3.2. Дифференциальные свойства задачи потребителя

89

Проверка уравнения Слуцкого для первого товара и второй цены состоит в проверке ра-

венства:

∂h1(p, x(p, R))

=

∂x1(p, R)

+

∂x1(p, R)x2(p, R)

.

∂p2

∂p2

∂R

Подставляя вычисленные производные, получим

2a2R

=

a2R

+

a2R

.

(p2 + a2p1)2

(p2 + a2p1)2

(p2 + a2p1)2

Очевидно, что это равенство верно.

4

Теорема 32 (свойства матрицы замены):

Пусть выполнены условия Теоремы 29, тогда матрица S = {∂hi } эффектов замены (мат-

∂pj

рица Слуцкого) является симметричной, отрицательно полуопределенной и вырожденной.

Доказательство: Как было отмечено выше при обсуждении леммы Шепарда, при сделанных нами предположениях функция расходов является дважды непрерывно дифференцируемой. Тогда, в силу теоремы Юнга19, ее смешанные вторые производные совпадают, т. е.

∂2e(p, x)		∂2e(p, x)
	=		.
∂pj∂pi		∂pi∂pj

С учетом продифференцированного тождество Шепарда, получаем отсюда, что

∂hi(p, x) = ∂hj(p, x). ∂pj ∂pi

Таким образом, матрица коэффициентов замены (матрица вторых производных функции расходов) рационального потребителя симметрична. Кроме того, поскольку функция расходов e(p, x) — вогнутая функция цен, то матрица коэффициентов замены является отрицательно полуопределенной. Вырожденность матрицы S читатель может доказать самостоятельно (см. задачу 125).

Теперь получим основные соотношения, которые связывают производные спроса по ценам и доходу.

Теорема 33:

Пусть x(p, R) — решение задачи потребителя. Предположим, также что x(p, R) — непрерывно дифференцируемая функция. Тогда выполнены следующие свойства:

Xi

(p, R)

pi

∂xi

+ xj(p, R) = 0

для всех j ;

∂pj

Xi

(p, R)

∂x (p, R)

pi

∂xk

+ R

k

= 0

для всех k;

∂pi

∂R

Xi

(p, R)

pi

∂xi

= 1.

∂R

Доказательство: Доказательство предоставляется читателю в качестве упражнения (см. задачу 130).

19 См. Приложение ??