7.6. Сравнительная статика решений в условиях неопределенности

262

Проиллюстрируйте анализ для простого случая, когда есть всего два состояния природы, на диаграмме (в системе координат «богатство в первом состоянии» — «богатство во втором состоянии»)11.

/ 399. [Аткинсон, Стиглиц] Докажите, что в ситуации, когда инвестору доступны приносящий доход безрисковый и рискованный активы, налог на валовой доход от портфельных инвестиций увеличивает (уменьшает, оставляет постоянным) частный риск (т. е. дисперсию доходности оптимального портфеля), если эластичность по доходу спроса на рискованный актив положительна (отрицательна, постоянна). Проиллюстрируйте его графически для случая двух состояний природы.

7.6Сравнительная статика решений в условиях неопределенности

Вэтом параграфе мы попытаемся ответить на следующие вопросы, относящиеся к сравнительной статике инвестиционного поведения

•какие условия на предпочтения инвестора гарантируют рост вложений в рискованную часть портфеля при росте величины суммарных инвестиций;

•какие условия на предпочтения двух инвесторов гарантирую большую величину вложений в рискованную часть портфеля одного из них при равных величинах суммарных инвестиций;

•какие свойства двух лотерей гарантируют, что одну их них всегда предпочитает любой другой инвестор, предпочтения которого представляются функцией полезности Неймана — Моргенштерна???.

Ответ на первые два вопроса формулируется в терминах характеристик отношения к риску, к анализу которых мы переходим.

Рассмотрим лотерейный билет, которой приносит чистый выигрыш ε1 с вероятностью µ и ε2 с вероятностью 1 − µ. Обозначим соответствующую случайную величину через ε˜. Потребитель, располагающий суммой денег ω, приобретет этот лотерейный билет, если лотерея, описываемая случайной величиной x˜ = ω + ε˜, предпочитается вырожденной лотерее, дающей ω с вероятностью 1, т. е.

E(u(ω + ε˜)) > u(ω).

или

µu(ω + ε1) + (1 − µ)u(ω + ε2) > u(ω).

Обозначим множество всех таких лотерейных билетов (ε1, ε2) (которые потребитель согласен приобрести) через E(ω).

Изобразим на плоскости (ε1, ε2) множество E(ω). Потребителю выгодно приобрести любой лотерейный билет, представленный точкой из I квадранта, и не выгодно приобретать любой лотерейный билет, представленный точкой из III квадранта. Выгодность приобретения билетов, представленных точками из II и IV квадрантов зависит, в частности, от отношения к риску рассматриваемого потребителя. Если элементарная функция полезности u(·) вогнута, то множество E(ω) выпукло. (Докажите это.)

Для любой лотереи, лежащей на границе этого множества, выполняется:
µu(ω + ε1) + (1 − µ)u(ω + ε2) = u(ω).	(E)

11Это упражнение опирается на методы сравнительной статики, которые используются в анализе влияния налогообложения на инвестиционные решения.

7.6. Сравнительная статика решений в условиях неопределенности

263

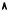ε2

E(ω)

ε1

ε2(ε1)

Рис. 7.7. Лотерейные билеты, которые потребитель готов приобрести

Это уравнение задает зависимость ε2 = ε2(ε1) в виде неявной функции. Стандартные свойства элементарной функции полезности и условие µ < 1 гарантируют существование такой функции и ее дифференцируемость. Подставим ε2 = ε2(ε1) в (E) и продифференцируем по ε1 в точке 0. Используя, тот факт, что ε2(0) = 0 получим

µu0(ω) + (1 − µ)u0(ω)ε02(0) = 0.

Это уравнение описывает касательную к E(ω) в точке (0, 0). Эта касательная имеет наклон −1−µµ . Поскольку выпуклое множество лежит выше своей касательной, то точки лежащие ниже этой касательной не принадлежат E(ω). Таким образом, если ε2 будет меньше, чем −1−µµ ε1 , то участник заведомо не примет участия в такой лотерее (какова бы ни была вероятность µ).

Рассмотрим двух рискофобов. Пусть первый из них принимает лотереи, принадлежащие множеству E1(ω), а второй — множеству E2(ω). Если E2(ω) E1(ω) (строгое включение), то естественно считать, что из этих двух рискофобов второй характеризуется б´ольшим неприятием риска, чем первый.

ε2

E1(ω)

E2(ω)

ε1

Рис. 7.8. Сравнение отношений к риску двух потребителей

Если ни одно из включений E2(ω) E1(ω) и E1(ω) E2(ω) не выполнено, то мы не можем проранжировать рассматриваемых участников, используя данное правило.

Заметим, что линейная аппроксимация этих множеств (полуплоскость, задаваемая касательной в нуле) одна и та же и не отражает различие в отношениях к риску. Поэтому следует рассмотреть «аппроксимацию второго порядка».

В предположении, что элементарная функция полезности дважды непрерывно дифференцируема, продифференцируем соотношение (E) по ε1 дважды в точке 0. Получаем

h

i

µu00(ω) + (1 − µ) u00(ω)(ε02(0))2 + u0(ω)ε002(0) = 0.

7.6. Сравнительная статика решений в условиях неопределенности										264
С учетом того, что ε0	(0) =	−	µ	, получим
			1−µ
2
				ε00(0) =		u00(ω) µ			.
					− u0(ω) (1 − µ)2
				2

Мы убедились, что уравнения границ множеств E1(ω) и E2(ω) в первом приближении всегда совпадают, а во втором приближении могут различаться. При этом, если ε002(0) у первого меньше, чем у второго, то в окрестности нуля E2(ω) содержится в E1(ω). (Понятно, что глобально это может не выполняться.) Поэтому величину −u00(ω)/u0(ω) можно рассматривать как локальную меру неприятия риска. Эти рассуждения мотивируют введение следующей характеристики предпочтений потребителя.

Определение 59:

Мерой неприятия риска Эрроу — Пратта называется величина

u00(x) ρ(x) = − u0(x) .

При определенных условиях эту меру неприятия риска можно рассматривать и как глобальную меру неприятия риска. В терминах меры Эрроу — Пратта из двух участников можно считать, что тот участник характеризуется б´ольшим неприятием риска, у которого мера Эрроу — Пратта всегда больше.

Предложенный Эрроу и Праттом подход — не единственный способ измерить отношение к риску. Выше мы ввели вознаграждение за риск, которую тоже можно рассматривать как меру

отношения к риску. Напомним, что величина	x(˜x) называется вознаграждением за риск для
данного потребительского набора x˜, если E x˜ −	x(˜x) является безрисковым эквивалентом x˜:

E u(˜x) = u(E x˜ − x(˜x)).

Также напомним, что для любого рискофоба вознаграждение за риск — величина неотрицательная. Естественно считать, что в терминах вознаграждения за риск из двух участников тот характеризуется большим неприятием риска, у которого вознаграждение за риск всегда больше.

Можно предложить еще один способ ранжирования рискофобов по их отношению к риску — «степень вогнутости» элементарной функцией полезности. Можно считать, что u(·) «более вогнута», чем v(·), если существует строго вогнутая строго возрастающая функция G(·) такая, что u(x) = G(v(x)) x, тогда участник с элементарной функцией полезности u(·) характеризуется большим неприятием риска.

Оказывается, что все эти способы ранжирования эквивалентны, о чем свидетельствует следующее утверждение.

Теорема 93 ((Теорема Пратта)):

Рассмотрим двух потребителей, предпочтения которых характеризуются дважды непре-

рывно дифференцируемыми элементарными функциями полезности u1(·) и u2(·), такими что u0i(x) > 0 и u00i (x) 6 0 x, i = 1, 2.

Следующие три условия эквивалентны:

(i) ρ1(x) > ρ2(x) x, где ρi(·) — мера неприятия риска Эрроу — Пратта, соответствующая ui(·).

(ii)Существует вогнутая возрастающая функция G(·) такая, что u1(x) = G(u2(x)) x.

(iii)Для всех случайных переменных x˜ с ненулевой дисперсией (Var(˜x) 6= 0) выполнено

x1(˜x) > x2(˜x).

7.6. Сравнительная статика решений в условиях неопределенности

265

Доказательство: (i) (ii)

Имеется функция G(·), такая что

u1(x) = G(u2(x)).

(При доказательстве утверждения в направлении (i) (ii) можем определить G(·) на области значений функции u2(·) следующим образом:

G(x) = u1(u−2 1(x)).

Поскольку u2(·) строго монотонна, то она обратима.)

Заметим, что функция G(·) является дважды непрерывно дифференцируемой и возрастающей. Дважды продифференцируем последнее соотношение:

u01(x) = G0(u2(x))u02(x),

u001(x) = G00(u2(x))u02(x) + G0(u2(x))u002(x).

Заметим, что из первого равенства следует, что G0(u2(x)) > 0. Поделив вторую производную на первую, получим

G00(u2(x))

−ρ1(x) = −ρ2(x) + G0(u2(x)) .

Поскольку G0(u2(x)) > 0, то ρ1(x) > ρ2(x) эквивалентно G00(y) 6 0 y = u2(x), то есть функция G(·) вогнута в своей области определения тогда и только тогда, когда ρ1(x) > ρ2(x) для всех x.

(ii) (iii)

Если функции u1(·) и u2(·) связаны между собой соотношением u1(x) = G(u2(x)) x, то для произвольной случайной величины x˜ по определению вознаграждения за риск имеют место равенства

u1(E x˜ − x1(˜x)) = E u1(˜x) = E G(u2(˜x)),

u1(E x˜ − x2(˜x)) = G(u2(E x˜ −	x2(˜x))) = G(E u2(˜x)).
Из монотонности u1(·) следует, что x1(˜x) >	x2(˜x) тогда и только тогда, когда u1(E x˜ −

x1(˜x)) 6 u1(E x˜ − x2(˜x)), т. е. тогда и только тогда, когда E G(u2(˜x)) 6 G(E u2(˜x)).

Если функция G(·) вогнута, то по неравенству Йенсена E G(u2(˜x)) 6 G(E u2(˜x)), и поэтому x1(˜x) > x2(˜x).

Наоборот, если x1(˜x) > x2(˜x), то выполнено неравенство E G(u2(˜x)) 6 G(E u2(˜x)), а это свойство эквивалентно вогнутости функции G(·). (Проверьте, что обычное определение вогнутой функции является частным случаем неравенства Йенсена.)

Введенная мера Эрроу — Пратта называется абсолютной мерой Эрроу — Пратта. Кроме того, рассматривают относительную меру Эрроу — Пратта, которая определяется по формуле:

u00(x)x − u0(x) .

Относительная мера Эрроу — Пратта является эластичностью предельной полезности (по доходу).

Меры Эрроу — Пратта являются полезными инструментами анализа поведения инвестора в условиях риска, так как в их терминах получаются ответы на стандартные вопросы сравнительной статики: как изменяется структура инвестиционного портфеля при изменении размера инвестиций, доходностей активов и т. д. А к проблемам сравнительной статики сводятся

7.6. Сравнительная статика решений в условиях неопределенности

266

многие проблемы прикладной экономики: характер спроса на деньги в портфельной теории формирования спроса на деньги, влияние налогообложения и т. д.

В терминах (абсолютной) меры Эрроу — Пратта можно охарактеризовать спрос на рискованный актив как функцию величины инвестиций в рассматриваемый портфель из двух активов.

U = E u(ωr0 + z(˜r − r0)) → max .

α>0

Мы предполагаем, что решение z(ω) существует ω R+ и что E r˜ > r0 , т. е. что решение внутреннее (z(ω) > 0).

Теорема 94:

Если мера Эрроу — Пратта ρ(x) убывает, то рискованный актив является нормальным благом, т. е. z0(ω) > 0.

Доказательство: Условие оптимальности портфеля имеет вид

E[u0(˜x)(˜r − r0)] = 0,

где x˜ = ωr0 + z(ω)(˜r − r0). Продифференцируем его по ω:

E[u00(˜x)(˜r − r0)(r0 + z0(ω)(˜r − r0))] = 0,

По свойствам оператора математического ожидания

r0 E[u00(˜x)(˜r − r0)] = −z0(ω) E[u00(˜x)(˜r − r0)2],

откуда

z0(ω) = −r0 E[u0000(˜x)(˜r − r0)] , E[u (˜x)(˜r − r0)2]

Ясно, что знаменатель здесь меньше нуля, так как в силу вогнутости функции полезности u00(x) < 0. Покажем, что числитель больше нуля.

Рассмотрим случайную величину r˜ − r0 : она принимает как положительные, так и отрицательные значения. Рассмотрим случай r˜ = r > r0 . В силу убывания функции ρ(·) при z > 0

ρ(ωr0 + z(r − r0)) < ρ(ω),

По определению меры Эрроу — Пратта

−u00(ωr0 + z(r − r0)) < ρ(ω), u0(ωr0 + z(r − r0))

Умножив это неравенство на знаменатель и на −(r − r0), получаем:

u00(ωr0 + z(r − r0)) > −ρ(ω)u0(ωr0 + z(r − r0)),

Легко видеть, что при r˜ = r < r0 это неравенство тоже верно. Это означает, что верно

соотношение

E u00(ωr0 + z(ω)(˜r − r0)) > −ρ(ω) E u0(ωr0 + z(ω)(˜r − r0)).

Следовательно, z0(ω) > 0. Другими словами, рискованный актив является нормальным благом.

Отметим, однако, что это свойство не выполняется для случая двух и более рискованных активов.