7.6. Сравнительная статика решений в условиях неопределенности

267

7.6.1Задачи

/ 400. Покажите, что если абсолютная мера Эрроу — Пратта неприятия риска убывает, то u000 6 0. Покажите, что обратное неверно.

/401. Приведите примеры элементарной функции полезности с возрастающей, убывающей и постоянной абсолютной и относительной мерой Эрроу — Пратта.

/402. Покажите, что при увеличении объема инвестиций доля инвестиций в рискованный актив (в сумме инвестиций в оптимальный портфель) постоянна (возрастает, убывает), если относительная мера Эрроу — Пратта убывает (возрастает, постоянна).

/403. Пусть в ситуации с двумя активами, рассмотренной выше, α(r0) — оптимальная доля вложений в рискованный актив как функция доходности безрискового актива. Покажите, что если для абсолютной меры Эрроу — Пратта выполнено ρ0(·) > 0 (она является возрастающей функцией), и решение внутреннее (0 < α(r0) < 1), то dα(r0)/dr0 > 0, т. е. уменьшение доходности безрискового актива приводит к увеличению доли вложений в рискованный актив.

Указание: Покажите, продифференцировав условие первого порядка, что

dα(r0) = E(u0(˜x)) − ω(1 − α(r0))E(u00(˜x)(˜r − r0)).
dr0	ωE(u00(˜x)(˜r − r0)2)

Отсюда следует требуемый результат, поскольку E(u00(˜x)(˜r − r0)) 6 0 (вследствие того, что

ρ0(·) > 0).

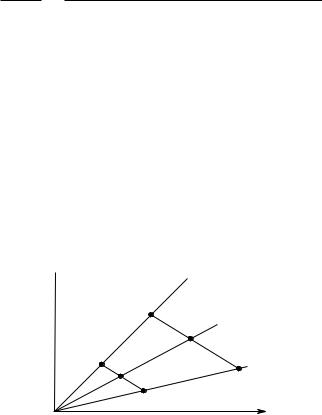
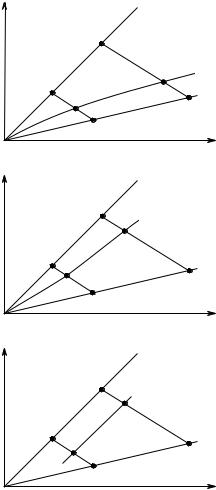
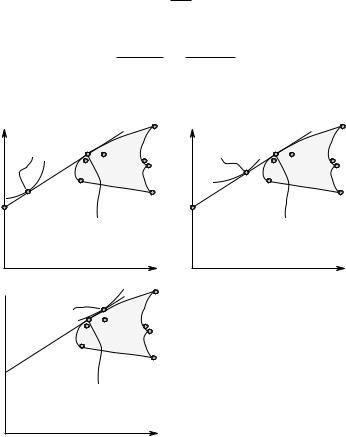
/ 404. Предположим, что (в мире с двумя состояниями) имеется один рискованный (с нормой доходности r˜) и один не приносящий дохода безрисковый актив. Охарактеризуйте в терминах относительной и абсолютной меры неприятия риска Эрроу — Пратта (эластичности по богатству спроса на рисковый актив) представленные на рисунке возможные структуры оптимальных портфелей при разных уровнях богатства. Линия P P 0 представляет совокупность фактических портфелей (при разных уровнях инвестиций в портфель), SS0 (T T 0 ) — совокупность портфелей при условии, что портфели содержат лишь безрисковые (рискованные) активы. Линии ST (S0T 0 ) представляют совокупность допустимых портфелей при данном уровне инвестиций.

(а)

r2

S0

P 0

S

P

T 0

T

r1

(б)

(в)

(г)

/405. Докажите, что если у двух индивидуумов меры неприятия риска ρ1(·) и ρ2(·) таковы, что при всех x выполнено ρ1(x) 6 ρ2(x), то для любого исходного уровня богатства ω выполнено E2(ω) E1(ω). (Заметим, что обратное утверждение фактически доказано в тексте параграфа.)

/406. Пусть x˜(t) — семейство случайных величин, принимающих значение ω + t и ω − t c равными вероятностями, и пусть Δ(t) — вознаграждение за риск для x˜(t) для потребителя

7.6. Сравнительная статика решений в условиях неопределенности

268

r2
	S0
		P 0
S
	P	T 0
	T	r1
r2
	S0	P 0
S	P
		T 0
	T	r1
r2
	S0	P 0
S	P
		T 0
	T	r1

с элементарной функцией полезности u(·), такой что u0(x) > 0 и u00(x) 6 0. Покажите, что

Δ(0) = 0, 0(0) = 0 и 00(0) = −u00(ω)/u0(ω) = r(ω).

/ 407. Пусть x˜(t) — семейство случайных величин, принимающих значение ω + t и ω − t c равными вероятностями, и пусть π(t) — вероятностное вознаграждение за риск для этих случайных величин, которое определяется по формуле

u(ω) =	1	+ π(t) u(ω + t) +	1		− π(t) u(ω − t).
	2		2

(A)Покажите, что если элементарная функция полезности u(·) строго вогнута, то π(t) > 0

при t > 0 и π(0) = 0.

(B)Покажите, что 4π0(0) = −u00(ω)/u0(ω) = r(ω).

/408. Рассмотрите лотереи вида ω + tε, где E ε = 0. Покажите, что в первом приближении (при малых t) премия за риск равна

ρ(ω) Var(ε)t2/2,

где ρ(·) — абсолютная мера Эрроу — Пратта.

7.7. Приложение: модель Марковица и CAPM

269

7.7Приложение: модель Марковица и CAPM12

Рассмотрим интересный частный случай модели инвестора, предположив, что элементарная функция полезности u(·) имеет вид параболы:

u(x) = a0 + a1x − a2x2.

(Можно интерпретировать это как квадратичную аппроксимацию первоначальной элементарной функции полезности получаемую разложением в ряд Тейлора вплоть до членов второго порядка в некоторой точке:

u(·) = α0 + α1x + α2x2 + . . .)

Предполагается, что здесь a1, a2 > 0. Условие a2 > 0 гарантирует, что инвестор является рискофобом. Условие a1 > 0 гарантирует, что при достаточно малых x элементарная функция полезности имеет положительную производную. Очевидно, что квадратичная функция может быть адекватной аппроксимацией не при всех x, поскольку при x = a1/(2a2) она достигает максимума, а далее убывает (т. е. по сути дела она подразумевает насыщаемость предпочтений инвестора)13.

u(x)=a0+a1x−a2x2

x

a1/(2a2)

Рис. 7.9. ???

При такой элементарной функции полезности ожидаемая полезность случайного дохода x˜ равна

U = E u(˜x) = a0 + a1 E x˜ − a2 E(˜x2).

12H. M. Markowitz: Portfolio Selection, The Journal of Finance 7 (1952): 77–91;H. M. Markowitz: Portfolio Selection: E cient Diversification of Investments, New York: John Wiley & Sons, 1959;J. Tobin: Liquidity Preference as Behaviour Towards Risk, Review of Economic Studies 25 (1958): 65–86;J. Tobin: The Theory of Portfolio Selection, in The Theory of Interest Rates, F. H. Hahn and F. P. R. Brechling (ed.), London: Macmillan, 1965: 3–51.

13У квадратичной функции есть и другие серьезные недостатки, вследствие чего модель Марковица нельзя считать вполне адекватной для описания инвестиционного поведения. Однако она вполне оправданна, если считать ее первым приближением с точки зрения моментов распределения. Очевидно, что если учитывать только первые моменты (ожидаемые доходности), то модель станет совсем неадекватной, поскольку не будет учитывать риск (см. об этом, например, в статье Г. Марковица). П. Самуэльсон показал (P. A. Samuelson: The Fundamental Approximation Theorem of Portfolio Analysis in terms of Means, Variances and Higher Moments, Review of Economic Studies 37 (1970): 537–542), что при малом риске, т. е. в пределе, при стремлении распределения доходностей активов r˜k к вырожденному распределению, при котором r˜k принимает значение r0 с вероятностью единица, приближение по двум первым моментам дает верное решение с точки зрения структуры портфеля. Если учесть более высокие моменты, то приближение будет более точным, но анализ модели существенно усложняется.

Другой случай (помимо квадратичной функции), при котором ожидаемая полезность зависит только от ожидаемой доходности и дисперсии доходности, — это когда доходности активов r˜k имеют (многомерное) нормальное распределение. Но нормальное распределение плохо аппроксимирует поведение доходностей реальных финансовых активов.

7.7. Приложение: модель Марковица и CAPM

270

Введем обозначения x¯ = E x˜ (ожидаемый доход) и σx2 = Var x˜ (дисперсия дохода). По определению дисперсии

E(˜x2) = (E x˜)2 + Var x˜ = x¯2 + σx2.

В этих обозначениях ожидаемая полезность примет вид

U = a0 + a1x¯ − a2(¯x2 + σx2).

Таким образом, при квадратичной элементарной функции полезности целевая функция инвестора зависит от двух характеристик распределения его дохода от портфеля: от математического ожидания дохода (среднего дохода) и дисперсии дохода (которую можно считать мерой рискованности). Эта парадигма «среднее-дисперсия» Марковица не только упрощает анализ инвестиционного поведения, но и позволяет давать наглядные геометрические интерпретации различных этапов такого анализа, поскольку каждый портфель в этой ситуации характеризуется всего двумя параметрами.

Удобно, как и выше, перейти от дохода к валовой доходности портфеля, которую обозначим через r˜P :

r˜P = x/ω˜ .

Обозначим через r¯P ожидаемую доходность портфеля, E r˜P , а через σP2 — дисперсию доходности портфеля, Var r˜P . Поскольку x˜ = ωr˜P , то, вынося константу ω за операторы мат. ожидания и дисперсии, получим

x¯ = E x˜ = E(ωr˜P ) = ω E r˜P = ωr¯P

и

σx2 = Var x˜ = Var(ωr˜P ) = ω2 Var r˜P = ω2σP2 .

Подставим эти выражения в функцию полезности:

U = a0 + a1ωr¯P − a2ω2(¯rP2 + σP2 )

или, при введении обозначений b0 = a0 , b1 = a1ω, b2 = a2ω2 ,

U = b0 + b1r¯P − b2(¯rP2 + σP2 ),

Мы можем нормировать эту функцию, применив к ней соответствующее линейное возрастающее преобразование. Окончательно получаем следующую функцию полезности:

U = r¯P − γ(¯rP2 + σP2 ).

Функция зависит от ожидаемой доходности портфеля и дисперсии доходности портфеля. Коэффициент γ отражает степень неприятия риска.

Доходность портфеля очевидным образом связана с доходностями активов:

X

r˜P = αkr˜k

k K

или

r˜P = α|˜r,

где α = {αk}k — вектор долей активов (структура портфеля), ˜r — вектор, составленный из доходностей активов. Таким образом, доходность портфеля — это взвешенное среднее доходностей активов, где в качестве весов выступают доли активов в портфеле.

7.7. Приложение: модель Марковица и CAPM

271

Обозначим через ¯r вектор, составленный из ожидаемых доходностей активов r¯k = E r˜k , а через V — ковариационную матрицу доходностей активов. В этих обозначениях для ожидаемой доходности портфеля выполнено соотношение

r¯P = E r˜P = E(α| ˜r) = α| E(˜r) = α| ¯r = X αkr¯k,

k K

(ожидаемая доходность портфеля — это взвешенное среднее ожидаемых доходностей активов), а для дисперсии доходности портфеля выполнено

σP2 = Var(˜rP ) = Var(α|˜r) = E[(α|˜r − E(α|˜r))2] =

= E[(α|˜r − α|¯r)2] = E[(α|(˜r − ¯r))2] = E[α|(˜r − ¯r)(˜r − ¯r)|α] =

= α| E[(˜r − ¯r)(˜r − ¯r)|]α = α|Vα =		αk1 αk2 ck1k2 .
kX1	X2
K k		K

Типичным элементом ковариационной матрицы V является ковариация между доходностями пары активов:

ck1k2 = Cov(˜rk1 , r˜k2 ) = E[(˜rk1 − r¯k1 )(˜rk2 − r¯k2 )].

Ковариационная матрица симметрична и по диагонали ее стоят дисперсии доходностей от-

дельных активов σk2 = ckk = Var r˜k .
[Напомним, что в дискретном случае величины r¯k , σk2 и ck1k2					вычисляются по формулам:
X		sX		X	− r¯k1 )(rk2s − r¯k2 )).]
r¯k =	µsrks, σk2 =	µs(rks − r¯k)2, ck1k2	=	µs(rk1s
s S		S		s S

Дисперсию доходности портфеля можно выразить также через корреляции доходностей акти-

вов:

σP2 = X X αk1 αk2 σk1 σk2 ρk1k2 ,

k1 K k2 K

где σk — корень из дисперсии (среднеквадратическое отклонение) доходности k-го актива, ρk1k2 — коэффициент корреляции доходностей активов k1 и k2 , определяемый как

ρk1k2 = ck1k2 .

σk1 σk2

В конечном итоге задача инвестора в модели Марковица приобретает следующий вид:

|¯
	|¯ 2	|	Vα	→	max .
U = α r	− γ (α r)	+ α			α
	αk 6 1,

X

k K

αk > 0, k K, k 6= 0.

Взависимости от рассматриваемой модели безрисковый актив k = 0 может присутствовать, либо нет в формулировке этой задачи инвестора. Эта задача представляет собой задачу квадратичного программирования, поскольку в нее входят только многочлены второго порядка от долей αk .

Втакой упрощенной модели выбора каждый актив характеризуется для инвестора всего двумя параметрами, поэтому задачу инвестирования можно и удобно рассматривать на диаграмме с осями σ, r¯ (диаграмма риск-доходность). На этой диаграмме каждый актив или портфель активов P можно изобразить точкой (σP , r¯P ).

7.7. Приложение: модель Марковица и CAPM

272

Кривые безразличия (линии уровня функции полезности) r¯P − γ(¯rP2 + σP2 ) = const

представляют собой окружности с центром в точке (σP , r¯P ) = 0, 21γ .

Мы будем в дальнейшем предполагать, что точка насыщения с доходностью 1/2γ находится выше доходностей всех доступных инвестору активов.

Для этой модели можно доказать ряд утверждений о характеристиках портфелей, характеризующих структуры допустимых и оптимальных портфелей в разных ситуациях (с точки зрения доходностей доступных инвестору активов).

Рассмотрим случай, когда портфель составлен из безрискового актива (k = 0) и одного рискованного актива (первого). Дисперсия доходности такого портфеля равна

σP2 = Var(α0r0 + α1r˜1) = Var(α1r˜1) = α12 Var(˜r1) = α12σ12.

Среднеквадратическое отклонение равно

σP = α1σ1,

т. е. при комбинировании безрискового и рискованного активов среднеквадратичное отклонение портфеля пропорционально среднеквадратичному отклонению рискованного актива, причем коэффициент пропорциональности равен доле вложений в рискованный актив.

Доходность же портфеля, очевидно, равна

rP = α0r0 + α1r¯1 = (1 − α1)r0 + α1r¯1 = r0 + α1(¯r1 − r0).

Таким образом, портфели (σP , r¯P ), соответствующие различным выпуклым комбинациям этих активов лежат на отрезке с концами в точках (0, r0) и (σ1, r¯1). Это множество допустимых портфелей для случая, когда кредит невозможен (т. е. инвестор не может выбрать α0 > 0). Если кредит доступен, то возможные комбинации лежат на луче, выходящем из (0, r0) и проходящем через (σ1, r¯1). Часть луча за точкой (σ1, r¯1) соответствует кредиту (α0 > 0). Этот луч — аналог бюджетной прямой для задачи инвестора.

r¯P
1/(2γ)	(σ1	,r¯1)
	оптимальный
r0	портфель
		σP

Рис. 7.10. Оптимальный портфель в случае двух активов

Оптимальному портфелю на графике соответствует точка, в которой кривая безразличия касается луча. Доли активов в оптимальном портфеле определяются отношением инвестора к риску (параметром γ ). Для того, чтобы оптимальный портфель был внутренним (в смысле α1 > 0), необходимо и достаточно, чтобы r¯1 > r0 . В случае же r¯1 6 r0 наклон луча будет отрицательный и оптимум будет достигаться при α1 = 0 (рискованный актив не войдет в портфель).

Перейдем теперь к рассмотрению портфелей, содержащих несколько рискованных активов. Мы выясним при различных частных предположениях о коррелированности доходностей активов, какова будет структура множества возможных портфелей и каким будет оптимальный портфель.

7.7. Приложение: модель Марковица и CAPM

273

Сначала рассмотрим случай, когда доходности всех рискованных активов жестко положительно коррелированны, то есть когда коэффициент корреляции между любой парой активов равен единице:

ρk1k2 = 1 ( k1, k2 6= 0)14.

При этом

X2

2

σP2 =

αk1

αk2 σk1

σk2

= αk1

σk1

αk2 σk2

=

αkσk

X1

X1

X2

X

k

k

k

k

k

откуда

X

σP =

αkσk.

k

(В матричном виде

	σ1σ1 · · ·	σlσ1	= σσ| ,
V =	...	...

σ1σl · · · σlσl

где σ = {σk}k — вектор корней из дисперсий активов. В этих обозначениях

σP2 = α| Vα = α| σσ| α = (α| σ)2.)

Для ожидаемой доходности вне зависимости от коррелированности выполняется

X

r¯P = αkr¯k.

k

Отсюда следует, что множество точек (σP , r¯P ) при неотрицательных долях αk есть выпуклая комбинация точек (σk, r¯k), соответствующих рассматриваемым активам:

X

(σP , r¯P ) = αk(σk, r¯k)

k

(риски складываются с весами α, как и доходности).

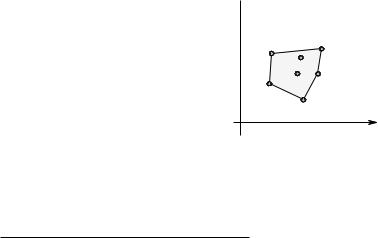
Другими словами, на диаграмме риск-доходность множество возможных рискованных портфелей представляет собой выпуклый многоугольник с вершинами в точках (σk, r¯k), соответствующих отдельным активам.

r¯P

σP

Рис. 7.11. Возможные рискованные портфели в случае жестко положительно коррелированных активов

Проанализируем структуру портфелей, содержащих дополнительно безрисковый актив.

14Такое может происходить, если доходности зависят от фазы экономического цикла или другого общего параметра.

7.7. Приложение: модель Марковица и CAPM

274

Выше мы уже рассмотрели, как комбинировать рискованный актив с безрисковым. Нетрудно понять, что по аналогичным формулам вычисляются характеристики портфеля, полученного при комбинировании рискованного портфеля с безрисковым активом. Любой такой портфель на диаграмме риск-доходность будет представлять собой точку отрезка (луча) соединяющего безрисковый актив с данным рискованным портфелем. Действительно, пусть доли активов в исходном рискованном портфеле равны νk , тогда этот портфель имеет следующие характеристики:

X

r¯R = νkr¯k,

k6=0

σR2 = X X νk1 νk2 ck1k2 .

k16=0 k26=0

Назовем комбинированным портфелем, состоящим из безрискового актива и исходного портфеля, с долями α0 и 1 − α0 соответственно, такой портфель, в котором доли вложений в рискованные активы равны αk = νk(1 − α0), а доля вложений в безрисковый актив равна α0 . Такой портфель имеет следующие характеристики:

	r¯P =		kX
			αkr¯k,
	kX1		K
		X2
σP2	=		αk1	αk2 ck1k2 .
	K k		K

Покажем, что выполнены следующие соотношения:

r˜P = α0r0 + (1 − α0)˜rR, σP = (1 − α0)σR,

r¯P = α0r0 + (1 − α0)¯rR,

то есть при таком комбинировании с портфелями можно обращаться так же, как с активами. (Этот результат можно обобщить на случай комбинирования любых портфелей.)

Действительно,

XX

r¯P = αkr¯k = α0r0 +	νk(1 − α0)¯rk =
k K	k6=0
kX	= α0r0 + (1 − α0)¯rR.
= α0r0 + (1 − α0) νkr¯k
K

Для дисперсии комбинированного портфеля имеем

σ2

=

X1

X2

=

α

k1

α

k2

c

k1k2

P

X16

k

K k K

kX16

X26

= α2c

X26

0

00

k1

0

k1

0

0

k2

0k2

k1 k2 k1k2

k =0

k =0

=0 k =0

Учитывая, что c00 = ck10 = c0k2 = 0, и αk = νk(1 − α0) получаем

σP2 = (1 − α0)2 X X νk1 νk2 ck1k2 = (1 − α0)2σR2

k16=0 k26=0

или

σP = (1 − α0)σR.

Вернемся к анализу портфеля, в котором все рискованные активы жестко положительно коррелированы. Учитывая полученный только что результат, охарактеризуем все комбинированные

7.7. Приложение: модель Марковица и CAPM

275

портфели в этом случае. Каждый из них является точкой на луче, выходящем из точки (0, r0) и проходящем через одну из точек многогранника рискованных активов. Таким образом, комбинированные портфели в данном случае представляют собой выпуклый конус, составленный из таких лучей. Оптимальный портфель должен лежать на верхней границе этого конуса, в точке, где ее касается кривая безразличия инвестора (см. Рис. 7.12).

r¯P оптимальный портфель

r0

σP

Рис. 7.12. Оптимальный портфель в случае жестко положительно коррелированных активов

В оптимальный портфель в невырожденном случае войдет только один рискованный актив, имеющий наилучшие характеристики.

Здесь рискованная часть портфеля определяется из задачи

r¯k − r0 → max .

σk k=1,...,l

Выбирается актив, для которого луч будет иметь наибольший наклон. Только он и может войти в портфель с положительным весом.

В вырожденном случае (см. Рис. 7.13) несколько активов характеризуются максимальным наклоном и все они могут войти в оптимальный портфель. В оптимуме относительные доли вложений в такие активы не определены однозначно.

r¯P

r0

σP

Рис. 7.13. Жестко положительно коррелированные активы — вырожденный случай

Мы рассматривали только поведение инвестора, т. е. спрос на активы, но можно рассматривать и предложение активов. Если те, кто предлагает активы, могут менять доходность, но не коэффициенты корреляции, то естественно ожидать, что в равновесии на рынке активов все предлагаемые активы лежат на оптимальном луче. Таким образом, для строго положительно коррелированных активов «вырожденный» случай в определенном смысле довольно естественен.

Второй случай коррелированности — жесткая отрицательная корреляция. Имеет смысл рассматривать только пару таких активов (для более чем двух активов все коэффициенты корреляции не могут равняться −1). Таким образом, пусть есть два актива, 1 и 2, такие что

7.7. Приложение: модель Марковица и CAPM					276
ρ12 = −1. Применяя общую формулу для расчета дисперсии, получим
P	σ1σ2	σ22	!	α2	!
σ2 = (α1, α2)	σ12	−σ1σ2		α1	=

−

= α12σ12 − 2α1α2σ1σ2 + α22σ22 = (α1σ1 − α2σ2)2,

откуда среднеквадратическое отклонение равно

σP = kα1σ1 − α2σ2k.

Ожидаемая доходность портфеля равна

r¯P = α1r¯1 + α2r¯2.

Несложно понять, что допустимые комбинации таких двух активов составляют ломаную. Точка излома соответствует портфелю с нулевым риском (σP = 0). Это означает, что из двух жестко отрицательно коррелированных активов можно составить безрисковый портфель.

r¯P безрисковый портфель

(σ1,r¯1)

(σ2,r¯2)

σP

Рис. 7.14. Возможные рискованные портфели в случае жестко отрицательно коррелированных активов

Чтобы получить такую ломаную на графике, нужно отразить одну из точек относительно вертикальной оси и соединить отрезком с другой точкой.

r¯P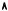

(σ1,r¯1)

(σ2,r¯2)

σP

Рис. 7.15. Построение ломаной возможных рискованных портфелей в случае жестко отрицательно коррелированных активов

Безрисковый портфель получается при следующей структуре портфеля:

α1 =	σ2		=	σ1
		, α2			.
	σ1 + σ2			σ1 + σ2

Его доходность, которую мы обозначим r00 , равна

r00 = σ1r¯2 + σ2r¯1 . σ1 + σ2

7.7. Приложение: модель Марковица и CAPM

277

Поскольку из двух таких активов можно составить безрисковый портфель, то рассматривать, как эти активы будут сочетаться с безрисковым активом, не имеет особого смысла. Можно сказать только, что при r00 > r0 и возможности кредита по ставке r0 получается парадоксальный результат — можно брать в кредит по ставке r0 и инвестировать без риска с доходностью r00 . При этом можно получить сколь угодно большую доходность портфеля. (Формально в модели решение существует, так как целевая функция насыщаема.) Ясно, что этого не может происходить в рыночном равновесии. Следует учесть предложение активов. Естественно предположить, что в равновесии должно быть r00 6 r0 (отсутствие «рога изобилия»).

Третий случай, который мы рассмотрим — некоррелированные активы. Тогда

V = diag(σ12, . . . , σl2). σP2 = α|Vα = X αk2σk2.

σP = s		k
	k	αk2σk2.
	X
Ожидаемая доходность портфеля, как всегда, равна
r¯P =		αkr¯k.
k
X

Из двух некоррелированных активов комбинируется дуга, изогнутая влево (см. Рис. 7.16). r¯P = α1r¯1 + α2r¯2 = α1r¯1 + (1 − α1)¯r2.

q q

σP = α12σ12 + α22σ22 = α12σ12 + (1 − α1)2σ22.

r¯P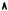

(σ1,r¯1)

(σ2,r¯2)

σP

Рис. 7.16. Возможные рискованные портфели в случае двух некоррелированных активов

В отличие от случая жесткой положительной коррелированности, риски при некоррелированности не складываются, поэтому риск при комбинировании активов будет снижен. Тогда все активы с доходностью выше гарантированной должны войти в оптимальный портфель (эффект диверсификации). Другими словами, для случая некоррелированных доходностей в модели Марковица выполняется аналог теоремы о диверсификации:

: Если доходности всех рискованных активов в модели Марковица некоррелированны, то рискованный актив войдет в оптимальный портфель (αk > 0), если, ?? и только если, его ожидаемая доходность выше гарантированной (r¯k > r0 ).

Доказательство этого утверждения будет приведено ниже.

7.7. Приложение: модель Марковица и CAPM

278

r¯P оптимальный а) портфель

(σ1,r¯1)

(σ2,r¯2)

r0

σP

r¯P	оптимальный	б)
	портфель
	(σ1,r¯1)
r0	(σ2	,r¯2)
		σP

Рис. 7.17. Оптимальные портфели в случае двух некоррелированных активов.

На Рис. 7.17а оба рискованных актива входят в оптимальный портфель, так как их ожидаемая доходность больше доходности безрискового актива. На Рис. 7.17б только один рискованный актив (1-й) входит в оптимальный портфель.

При произвольном коэффициенте корреляции комбинации доходности и риска, достижимые комбинированием двух активов, окажутся на графике некоторой кривой соединяющей эти точки и выгибающейся, при неполной коррелированности, влево. На Рис. 7.18 показаны портфели, которые можно составить из двух активов при разных коэффициентах корреляции. Чем меньше коэффициент корреляции, тем сильнее влево выгибается кривая возможных портфелей.

r¯P

ρ12=0

ρ12=−1 (σ1,r¯1)

ρ12=1

ρ12=−0,5 (σ2,r¯2)

ρ12=0,5

σP

Рис. 7.18. Возможные портфели из двух рискованных активов при разных коэффициентах корреляции

В общем случае допустимое множество R всех доступных инвестору портфелей, состоящих из рискованных активов, на диаграмме риск-доходность будет изображаться некоторой связной фигурой, граница которой оказывается кривой, выпуклой влево (см. напр. Рис. 7.19)15. Очевидно, что множество R лежит в пределах, задаваемых наибольшей и наименьшей ожидаемой доходностью доступных активов. Т. е. для любого рискованного портфеля (σM , r¯M ) R выполнено

min r¯k 6 r¯M 6 max r¯k.

Если бы инвестор выбирал портфель из множества R, то он не стал бы выбирать такой портфель (σM , r¯M ), для которого существует другой допустимый портфель (σM0 , r¯M0 ) R с лучшими характеристиками, т. е. такой что

σM0 6 σM и r¯M0 > r¯M ,

15Диаграмма изображает множество возможных портфелей, составленных из 7 активов, при некоторой матрице корреляций доходностей этих активов.

7.7. Приложение: модель Марковица и CAPM

279

r¯P

R

эффективная

граница

σP

Рис. 7.19. Множество возможных рискованных портфелей для нескольких активов

причем одно из неравенств строгое. Выбор инвестора всегда лежал бы на эффективной границе, состоящей из портфелей, для которых при заданной величине риска доходность максимальна (см. Рис. 7.19).

Комбинируя рискованные портфели с безрисковым активом получим множество всех возможных портфелей, которое на диаграмме будет выглядеть как конус с вершиной в точке (0, r0) (см. Рис. 7.20). Этот конус состоит из всех таких лучей, что они выходят из точки (0, r0) и проходят через одну из точек (σM , r¯M ) R.

r¯P	эффективный
	луч
	R
r0	рыночный
	портфель
	σP

Рис. 7.20. Множество возможных портфелей для нескольких активов

Комбинируя наилучшую (по наклону луча) точку из R с безрисковым активом, как и ранее получаем наилучший по соотношению риска и доходности. Оптимальный портфель определяется наиболее крутым лучом (см. Рис. 7.20), т. е.

	r¯M − r0	→	max .
	σM
			(σM ,r¯M )R

Полезность инвестора от оптимального портфеля равна

U = r¯P − γ(¯rP2 + σP2 ),

где величины r¯P и σP2 можно выразить через доли всех активов, кроме безрискового, (αk , k = 1, . . . , l) следующим образом:

l

X

r¯P = r0 + αk(¯rk − r0),

k=1

ll

σP2 = X X αk1 αk2 ck1k2 .

k1=1 k2=1

7.7. Приложение: модель Марковица и CAPM				280
Заметим, что
	∂r¯P		∂σP2	l
				jX
	∂αk	= r¯k − r0 и ∂αk
				= 2 αjcjk.
				=1

Будем рассматривать полезность U как функцию долей всех рискованных активов. Оптимальный портфель характеризуется долями, максимизирующими эту функцию (при ограничениях на их неотрицательность).

Найдем производную U по αk :

	∂αk	= ∂αk − γ 2¯rP		∂αk +	∂αk !		=
	∂U		∂r¯P	∂r¯P	∂σP2
= r¯k − r0 − γ 2¯rP (¯rk − r0) + 2					l	αjcjk =
					jX
					l
					=1
				jX
	= (1 − 2γr¯P )(¯rk − r0) − 2γ				αjcjk.
					=1

Для оптимального портфеля ∂U/∂αk 6 0, причем для активов, входящих в портфель (αk > 0), по условию дополняющей нежесткости, ∂U/∂αk = 0.

Из условий дополняющей нежесткости

l

X ∂U

k=1 αk ∂αk = 0,

т. е.

(1 − 2γr¯P )(¯rP − r0) − 2γσP2 = 0,

откуда, исключая обсуждавшийся выше вырожденный случай, когда σP2 = 0, получим

		1 −	2γr¯P =			2γσ2
							P
								,
						r¯P − r0
Отсюда		= 2γ σP2 r¯P			− r0		− αjcjk .
	∂αk
	∂U			r¯k	r0		l
					−		jX
							=1

Взвешенная сумма ковариаций в этой формуле равна:

l	l	l
X	jX	X
	αjcjk =	αj Cov(˜rj, r˜k) = Cov( αjr˜j, r˜k) =
j=1	=1	j=1

= Cov(˜rP − α0r0, r˜k) = Cov(˜rP , r˜k).

Обозначим эту величину cP k . Тогда
	∂U		= 2γ σP2	r¯k	r0	− cP k .
				r¯P	−
∂αk					r0
					−

Следовательно, условия первого порядка ∂U/∂αk 6 0, характеризующие оптимальный портфель, можно записать следующим образом:

σ2 r¯k − r0 6 cP k,

P r¯P − r0

7.7. Приложение: модель Марковица и CAPM

281

причем если k-й актив входит в оптимальный портфель (αk > 0), то здесь достигается равенство. Т. е. для активов, входящих в портфель, выполнено следующее условие оптимальности:

cP k

r¯k − r0 = σP2 (¯rP − r0).

Пусть ν = (ν1, . . . , νl) — структура рискованной части портфеля. Величина νk представляет собой долю вложений в k-й актив в общих вложениях в рискованные активы. Другими словами, если (α1, . . . , αl) — оптимальный для инвестора портфель, то

αk

νk = Pj6=0 αj , k =6 0.

В знаменателе стоит Pj6=0 αj = 1 − α0 — доля рискованной части портфеля. Можно записать это соотношение и в другом виде:

αk = νk(1 − α0), k 6= 0.

Рассмотрим портфель, составленный только из рискованных активов, с долями νk . Его доходность обозначим через r˜M . Она связана с доходностью полного оптимального портфеля как

r˜P = α0r0 + (1 − α0)˜rM .

Следовательно,

r¯P = α0r0 + (1 − α0)¯rM , σP2 = (1 − α0)2σM2 ,

cP k = Cov(˜rP , r˜k) = Cov((1 − α0)˜rM , r˜k) =

= (1 − α0) Cov(˜rM , r˜k) = (1 − α0)cMk.

Используя эти обозначения, условия первого порядка для актива, входящего в оптимальный портфель, можно записать как

r¯k − r0 = βk(¯rM − r0),

где
βk =	Cov(˜rM , r˜k)	=	cMk	.
	Var(˜rM )
			σM2

Это основная формула модели CAPM 16. В соответствии с этим соотношением ожидаемую доходность актива, вошедшего в портфель, можно разбить на две части:

1)доходность безрискового актива, r0 (это компенсация за отложенное потребление);

2)компенсация за подверженность риску, r¯k − r0 (премия за риск).

Коэффициент βk — это ковариация между доходностью k-го актива и доходностью рискованной части оптимального портфеля, нормированная на дисперсию доходности рискованной части оптимального портфеля. Такой нормированный показатель называется величиной бета этого актива.

Для активов, не входящих в оптимальный портфель, выполнено

r¯k − r0 6 βk(¯rM − r0).

В частном случае, когда доходности рискованных активов некоррелированны?? между собой, очевидно, что беты всех активов, не вошедших в оптимальный портфель, будут равны нулю. Следовательно, для актива, не вошедшего в портфель, выполнено

r¯k − r0 6 βk(¯rM − r0) = 0.

16См. напр., статью Уильяма Шарпа W. F. Sharpe: Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, Journal of Finance 19 (1964): 425–442.

7.7. Приложение: модель Марковица и CAPM

282

С другой стороны, если актив вошел в портфель, то его бета должна быть положительна. Следовательно, для такого актива

r¯k − r0 = βk(¯rM − r0) > 0

(где мы предполагаем, что r¯M > r0 ). Тем самым, мы доказали «теорему о диверсификации», сформулированную выше.

Интерпретируем теперь полученные результаты в контексте ситуации, когда всем инвесторам на рынке доступны одни и те же активы.

1) Множество R допустимых комбинаций рискованных активов у всех будет одним и тем

же.

2) Поскольку оптимальный портфель у каждого инвестора лежит на луче с наибольшим наклоном, выходящим из точки (0, r0) и проходящем через точку множества R, то у всех инвесторов рискованная часть портфеля будет иметь одно и то же соотношение (¯rM −r0)/σM . Рискованный портфель, характеризующийся этим оптимальным соотношением называется рыночным портфелем (см. Рис. 7.21). Это точка «касания» эффективного луча и множества R. Ясно, что всякая точка (σP , r¯P ), лежащая на эффективном луче удовлетворяет уравнению

r¯P = r0 − σP (¯rM − r0) σM

или

r¯P − r0 = r¯M − r0 , σP σM

где (σM , r¯M ) — характеристики рыночного портфеля.

r¯P	оптимальный	r¯P	оптимальный
	портфель		портфель
	R		R
r0	рыночный	r0	рыночный
	портфель		портфель
	σP		σP

r¯P оптимальный портфель

R

r0

рыночный

портфель

σP

Рис. 7.21. Оптимальные портфели разных инвесторов

: Теорема о разделении (Separation Theorem):

Для всякого инвестора (независимо от γ ) рискованная часть оптимального портфеля является рыночным портфелем.

7.7. Приложение: модель Марковица и CAPM

283

Соответственно, процесс поиска оптимального портфеля можно разделить на два этапа: сначала определяется оптимальный рискованный портфель (σM , r¯M ), а затем в зависимости от склонности к риску выбирается его оптимальное сочетание с безрисковым активом. При отождествлении оптимального рискованного портфеля с рыночным задачу первого «решает» рынок и инвестору достаточно выбрать соотношение между безрисковым активом и этим портфелем. Тем самым, вместо того, чтобы рассматривать все активы, инвестору достаточно выбрать соотношение между безрисковым активом и рыночным портфелем. (Выше мы уже анализировали подобную задачу.)

Это утверждение называют также «теоремой о взаимных фондах» (“Mutual Fund Theo¨ rem”). Название отражает тот факт, что в «мире Марковица» инвесторы могут доверить составление оптимального портфеля рискованных активов инвестиционным организациям («взаимным фондам»), а сами должны будут лишь комбинировать этот готовый портфель с безрисковым активом в соответствии со своими предпочтениями.

Как мы видели, точка касания (σM , r¯M ), вообще говоря, может быть не единственной. Кроме того, в общем случае данной паре (σM , r¯M ) не всегда соответствует единственная структура активов, поэтому рыночный портфель может быть не единственным.

Если мы имеем дело с невырожденным случаем (например, когда матрица корреляций доходностей рискованных активов невырождена), то рыночный портфель (ν1, . . . , νl) единственный и вектор (ν1, . . . , νl) для любого инвестора характеризует структуру рискованной части портфеля. Таким образом, этот же вектор характеризует структуру продаж активов на рынке в целом (отсюда и термин «рыночный портфель»).

Показатель бета отдельного актива, βk = cMk/σM2 , представляет собой характеристику актива, общую для всех инвесторов. Бета актива измеряет степень взаимосвязанности доходности актива и доходности рыночного портфеля. Соотношения

r¯k − r0 = βk(¯rM − r0).

показывают, что премия за риск, r¯k − r0 , пропорциональна коэффициенту βk . Коэффициент пропорциональности здесь — премия за риск для рыночного портфеля, r¯M − r0 .

Бета актива, фактически, представляет собой наклон теоретической линии регрессии доходности актива по доходности рыночного портфеля (отсюда и название). Действительно, можем ввести обозначение ε˜k = r˜k − r0 − βk(˜rM − r0) для ошибки регрессии. Тогда уравнение регрессии будет иметь вид

r˜k = (1 − βk)r0 + βkr˜M + ε˜k,

где ошибка имеет нулевое математическое ожидание E ε˜k = r¯k − r0 − βk(¯rM − r0) = 0 и некоррелирована с регрессором:

Cov(˜εk, r˜M ) = E(˜εkr˜M ) = E(˜rkr˜M ) − r0r¯M − βk(E(˜rM2 ) − r¯0r¯M ) =

= E(˜rkr˜M ) − r¯kr¯M − βk(E(˜rM2 ) − r¯M2 ) = cMk − βkσM2 = 0.

(См. Рис. 7.22.)

Отметим несколько свойств приведенных равновесных соотношений и коэффициентов бета. Ожидаемая доходность актива с нулевой бетой (т. е. актива, доходность которого некоррелированна с рыночной доходностью) равна безрисковой ставке, r0 . Поскольку такой актив не изменяет риск рыночного портфеля, то он, по сути дела, является безрисковым (несмотря на

то, что дисперсия доходности может быть положительной).

Актив с бетой равной единице эквивалентен рыночному портфелю и обладает той же ожидаемой доходностью, что и рыночный портфель.

Определим бету произвольного портфеля следующим образом:

Cov(˜rP , r˜M ) cMP

βP = Var(˜rM ) = σM2 .