16.7. Игры и Парето-оптимальность

680

Существует теорема (в англоязычной литературе она известна под названием Folk Theorem, что на русский можно перевести как «Народная теорема»), утверждающая, что в бесконечно повторяющейся конечной статической игре с полной информацией любой «разумный» вектор выигрышей может возникнуть в некотором совершенном в подыграх равновесии, если дисконтирующие множители достаточно близки к единице. Под разумным вектором выигрышей мы понимаем такой вектор выигрышей, который является выпуклой комбинацией выигрышей исходной игры (с точностью до множителей 1 − δi , необходимых для того, чтобы сделать выигрыши сопоставимыми), и кроме того, в нем каждый элемент должен быть не меньше некоторой пороговой величины. В разных вариантах теоремы пороговая величина разная: это либо выигрыш в каком-либо равновесии Нэша исходной игры, либо минимаксный выигрыш38.

Эту теорему можно интерпретировать как утверждение о том, что в бесконечно повторяющейся игре «почти все возможно». Кроме того, из теоремы можно сделать вывод, что в бесконечно повторяющейся игре совершенных в подыграх равновесий бывает, как правило, «слишком много». Понятно, что это снижает ценность полученного выше результата о возникновении сотрудничества в игре Ауманна.

16.7.2Игры торга

Теперь мы рассмотрим важный класс игр, моделирующих достижение соглашений между экономическими субъектами, — так называемые игры торга. В таких играх в условиях полной информации решения всегда Парето-оптимальны.

Игра 15. «Торг»39

Два игрока (A и B ) делят между собой некоторую сумму денег (или любое бесконечно делимое благо). Будем считать, что общее количество равно 1. Дележ можно задать долей, x [0, 1], достающейся игроку A. Если игрок A получает x, то игрок B , соответственно, получает 1 − x. Торг происходит в несколько раундов. На каждом раунде один из игроков предлагает дележ xj , где j — номер раунда. Другой игрок может либо отклонить, либо принять этот дележ. Если дележ принимается, то торг заканчивается и игроки получают свои доли (xj, 1 − xj). Если дележ отклоняется, то настает очередь другого игрока предложить свой дележ. Игрок A предлагает дележ в раундах с нечетными номерами, а игрок B — в раундах с четными номерами. Если за n раундов игроки не договорятся, то игра заканчивается и каждый игрок получает 0.

Предполагается, что игроки предпочитают получить деньги как можно раньше, поэтому полученная сумма денег умножается на дисконтирующий множитель, то есть если игроки договорятся на j -м раунде, то их выигрыши составят δAj−1xj и δBj−1(1 − xj) соответственно, где δA, δB (0, 1) — дисконтирующие множители.

J

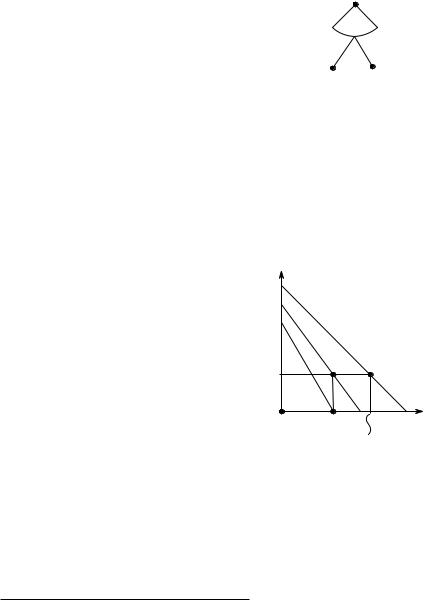
Рассмотрим эту игру при n = 3. На Рис. 16.30 показано дерево игры.

				Проанализируем эту игру, используя обратную индукцию. В
Игрок A				последнем раунде игрок B заведомо примет предложение игрока
	x1			A, если δB2 (1 − x3) > 0, т. е. если x3 < 1. Если x3 = 1, то игроку
Игрок B				B все равно, принять или отклонить предложение. Игроку A
				выгодно назвать x3 как можно б´ольшим. Значит, в равновесной
			x1	стратегии не может быть x3 < 1, ведь игрок A тогда мог бы
Игрок B			1−x1	немного увеличить x3 , не изменив выбора игрока B , и увеличил
	x2			бы при этом свой выигрыш. Таким образом, в равновесии x3 = 1.
Игрок A				Чтобы при этом действительно было равновесие, игрок B должен
			δAx2	в своей стратегии быть «благожелательным» по отношению к
Игрок A		δB(1−x2)		A, то есть принять его предложение; в противном случае игрок
	x3			A мог бы предложить x3 меньше 1 и увеличить при этом свой
Игрок B				выигрыш.
		δA2 x3
0				Анализ 3-го раунда показывает, что игрок A должен будет
0		δB2 (1−x3)		предложить x3 = 1, а игрок B должен будет принять этот де-

38См. J. W. Friedman: A Non-cooperative Equilibrium for Supergames, Review of Economic Studies 38 (1971):

1–12.

Рис. 16.30.

39A. Rubinstein: Perfect Equilibrium in a Bargaining Model, Econometrica 50 (1982): 97–109.

16.7. Игры и Парето-оптимальность

681

леж. Мы можем теперь «свернуть» игру, заменив 3-й раунд на конечный узел с выигрышами δA2 и 0.

Во 2-м раунде игрок A выбирает между δA2 (если отклоняет предложение) и δAx2 (если принимает). Таким образом, если x2 > δA , то он примет предложенный дележ, а если x2 < δA ,

то отклонит. При x2 = δA игроку A все равно, какой выбор сделать. Игрок B предпочтет получить выигрыш δB(1 −x2), а не 0, поэтому он не станет предлагать x2 < δA . С другой стороны любой дележ x2 > δA не является равновесным, поскольку игрок B в этом случае может уменьшить x2 , не меняя выбора игрока A, и, тем самым, увеличить свой выигрыш. Таким образом, в равновесии x2 = δA . Чтобы этот выбор был равновесным, требуется, чтобы в равновесии игрок A принял дележ x2 = δA , несмотря на то, что отказ от этого дележа должен принести ему такой же выигрыш40.

Остается торг, состоящий из одного раунда, в котором игроки получат δA2 и δB(1 − δA), если не придут к соглашению (см. Рис. 16.31). Рассуждения, аналогичные приведенным выше, показывают, что уже в первом раунде игроки придут к соглашению: игрок B примет дележ x1 = 1 − δB(1 − δA), предложенный игроком A. Выигрыши при этом составят 1 − δB(1 − δA) и δB(1 − δA).

Игрок A
	x1
	Игрок B
δA2	x1
δB(1−δA)	1−x1

Рис. 16.31.

Оторге в условиях полной информации можно сделать два замечания:

1)Торг заканчивается на первом раунде.

2)Равновесный исход Парето-оптимален.

Рис. 16.32 показывает графический способ нахождения равновесия в игре «Торг» при n = 3. На этом графике видно, как изменяется граница Парето от раунда к раунду, сжимаясь в сторону начала координат из-за дисконтирования. Процесс нахождения решения изображен толстой кривой, выходящей из начала координат.

u2
1
δB(1−δA)
	u1
δA2	1
1−δB(1−δA)
Рис. 16.32. ??

Задачи

/ 710. Постройте по своему имени и фамилии игру, как это описано в задаче 682 на с. 645. Найдите в этой игре границу Парето. Есть ли среди равновесий Нэша Парето-оптимальные?

40Это довольно естественно, если взглянуть на ситуацию с той точки зрения, что игрок B всегда может предложить игроку A дележ x2 = δA − ε, где ε — малое положительное число, тем самым гарантируя, что A примет дележ. Число ε здесь можно выбрать произвольно малым.

16.7. Игры и Парето-оптимальность

682

/711. Объясните, почему в антагонистической игре (игре, в которой сумма выигрышей игроков — постоянная величина) любой исход является Парето-оптимальным.

/712. Объясните, в чем состоит аналогия между аукционом, в котором игрок платит названную им цену, и игрой Ауманна (дилеммой заключенных). Представьте аукцион с двумя участниками как игру и сравните множество равновесий Нэша с границей Парето.

/713. Рассчитайте общие выигрыши (в каждой из конечных вершин) в повторяющейся дважды игре Ауманна, изображенной на Рис. 16.29, считая, что дисконтирующие множители обоих игроков равны

1/2.

/714. При каких значениях дисконтирующих множителей пара стратегий следующего вида41 будет совершенным в подыграх равновесием в повторяющейся игре Ауманна: «В первом раунде сотрудничать. В остальных раундах поступать так же, как другой игрок в предыдущем раунде»?

/715. Найдите совершенное в подыграх равновесие в бесконечно продолжающемся торге. Решение может опираться на тот факт, что через каждые два раунда подыгра, начинающаяся с текущей вершины, повторяет исходную игру с точностью до дисконтирования. Таким образом, естественно искать стационарное равновесие. Найдите такое равновесие и покажите, что оно является совершенным в подыграх равновесием. Будет ли это равновесие оптимальным по Парето?

41По-английски эту стратегию называют tit-for-tat, что может означать как «око за око», так и «услуга за услугу», а если обобщенно, то «платить той же монетой».

s s s s s s s s s s s s s s s s s s s s s s s s s s s s s				Глава
Математическое				17
приложение

»»»»>

17.1Вогнутые и квазивогнутые функции

Будем предполагать, что X — подмножество Rn .

Определение 97:

Функция f(·): X 7→R называется вогнутой, если X выпукло и для всех x, y X и α [0, 1] выполнено

f(αx + (1 − α)y) > αf(x) + (1 − α)f(y).

Функция f(·) называется выпуклой, если −f(·) вогнута.

Определение 98:

Функция f(·): X 7→R называется строго вогнутой, если X выпукло и для всех x, y X , таких что x 6= y и α (0, 1) выполнено

f(αx + (1 − α)y) > αf(x) + (1 − α)f(y).

Функция f(·) называется строго выпуклой, если −f(·) строго вогнута.

Заметим, что строго вогнутая функция является вогнутой. Линейная функция p| x является примером вогнутой, но не строго вогнутой функции.

Теорема 161:

Функция f(·): X 7→R является вогнутой тогда и только тогда, когда X выпукло и для всех

x

, . . . , x

X

α , . . . , α

0

что

k

α

= 1

1

k

и

1

k >

, таких

k

Pj=1

j

k

, выполнено

X

X

f

αjxj

> αjf(xj).

j=1

j=1

Данное свойство (как и определение вогнутой функции) является частным случаем неравенства Йенсена: f(E x˜) > E f(x˜) (для таких случайных величин, x˜ , у которых соответствующие математические ожидания существуют, в частности, для дискретных случайных величин).

Определение 99:

Верхним лебеговским множеством (superlevel set) функции f(·): X 7→R, соответствующим уровню

t R называется множество x X f(x) > t .

Теорема 162:

Всякое верхнее лебеговское множество вогнутой функции выпукло.

Заметим, что это необходимое, но не достаточное условие вогнутости функции. Например, всякое верхнее лебеговское множество функции x3 выпукло, но сама она не вогнута (при x > 0 она строго выпукла, что несовместимо с вогнутостью). Указанное свойство является необходимым и достаточным для квазивогнутых функций, о которых речь ниже.

Определение 100:

Подграфиком функции f(·): X 7→R называется множество (x, t) x X, t 6 f(x) .

683

17.1. Вогнутые и квазивогнутые функции

684

Теорема 163:

Подграфик функции является выпуклым множеством тогда и только тогда, когда функция

вогнута.

Теорема 164:

Пусть fj(·): X 7→R (j = 1, . . . , m) — вогнутые функции. Тогда

m

0

j=1 αjfj(x), где α1, . . . , αk >

вогнута.

, — вогнутая функция. В частности, сумма вогнутых функций

P

m

Пусть fj(·): X 7→R (j = 1, . . . , m) — строго вогнутые функции. Тогда

j=1 αjfj(x), где

α , . . . , α

k >

0

и

α

> 0

хотя бы для одного

j

частности, сумма

1

j

, — строго вогнутая функция. ВP

строго вогнутых функций строго вогнута.

Теорема 165:

Пусть fj(·): X 7→R (j = 1, . . . , m) — вогнутые функции. Тогда их поточечный минимум minj=1,...,m fj(x) — вогнутая функция.

Аналогичное свойство верно и в общем случае (не обязательно конечного) семейства вогнутых функций.

Теорема 166:				x
j = 1, . . . , m
Пусть f(x, y): X 7→R (m		) — семейство вогнутых по			функций, зависящих от
параметра y Y (где Y R	). Тогда их поточечный инфимум g(x) = infy Y f(x, y) — вогнутая
функция с областью определения x X			infy Y f(x, y) > −∞ .

Теорема 167:

Пусть g(·): X 7→R — вогнутая функция и ее область значений Y является выпуклым множеством, и пусть h(·): Y 7→R — вогнутая неубывающая функция. Тогда суперпозиция этих функций f(x) = h(g(x)) — вогнутая функция.

Теорема 168:

Пусть множество X является открытым, а функция f(·): X 7→R дифференцируема (т. е. во всех точках X существует ее градиент rf(·)). Эта функция является вогнутой тогда и только тогда, когда ее множество определения X выпукло и для всех x, y X выполнено неравенство

f(y) 6 f(x) + rf(x)|(y − x).

Т. е. вогнутая функция лежит (не строго) ниже любой своей касательной.

Теорема 169:

Точка x int(X) является минимумом дифференцируемой вогнутой функции f(·): X 7→R тогда и только тогда, когда rf(x) = 0.

Теорема 170:

Пусть множество X является открытым, функция f(·): X 7→R дважды дифференцируема (т. е. во всех точках X существует ее матрица Гессе r2f(·)). Эта функция является вогнутой тогда и только тогда, когда ее множество определения X выпукло и для всех x X ее матрица Гессе r2f(x) отрицательно полуопределена.

Теорема 171:

Пусть множество X является открытым. Если функция f(·): X 7→R дважды дифференцируема и ее матрица Гессе r2f(x) отрицательно определена для всех x X , то f(·) строго вогнута.

Заметим, что обратное, вообще говоря, неверно. Так, функция f(x) = −x4 является строго вогнутой, но f00(0) = 0.

Теорема 172:

Выпуклая (вогнутая) функция f(·): X 7→R непрерывна на внутренности ее множества определения int(X).

17.1. Вогнутые и квазивогнутые функции

685

Определение 101:

Функция f(·): X → R называется квазивогнутой, если X выпукло и для всех x, y X и α [0, 1] выполнено

f(αx + (1 − α)y) > min(f(x), f(y)).

Определение 102:

Функция f(·): X → R называется строго квазивогнутой, если для всех x, y X , таких что x 6= y, и α (0, 1) выполнено

f(αx + (1 − α)y) > min(f(x), f(y)).

Определение 103:

Функция f(·) называется квазивыпуклой, если −f(·) квазивогнута.

Определение 104:

Функция f(·) называется строго квазивыпуклой, если −f(·) строго квазивогнута.

Теорема 173:

Всякое верхнее лебеговское множество квазивогнутой функции выпукло.

???

Теорема 174:

Непрерывная функция f(·): X 7→R, где X R, является квазивогнутой тогда и только тогда, когда ее множество определения X выпукло, и выполнено по крайней мере одно из трех условий:

•функция f(·) является неубывающей;

•функция f(·) является невозрастающей;

•существует точка x X , такая что на множестве X ∩ (−∞, x ] функция f(·) является

неубывающей, а на на множестве X ∩ [x , +∞) — невозрастающей.

Теорема 175:

Пусть g(·): X 7→R — квазивогнутая функция с областью значений Y , и пусть h(·): Y 7→ R — неубывающая функция. Тогда суперпозиция этих функций f(x) = h(g(x)) — квазивогнутая функция.

Теорема 176:

Пусть множество X является открытым, и функция f(·): X 7→R дифференцируема. Эта функция является квазивогнутой тогда и только тогда, когда ее множество определения X выпукло, и для всех x, y X , таких что f(y) > f(x), выполнено неравенство

rf(x)|(y − x) > 0.

Заметим, что для квазивогнутой функции (в отличие от вогнутой) из rf(x) = 0 не следует, что точка x является максимумом этой функции.

Теорема 177:

Пусть множество X является открытым. Если функция f(·): X 7→R дважды дифферен-

цируема и квазивогнута, то для всех	x X и p Rn , таких что p| rf(x) = 0, выполнено
p| r2f(x)p 6 0.	2	f(x) дважды дифферен-
Как следствие, для всех x X , таких что rf(x) 6= 0, матрица Гессе r

цируемой и квазивогнутой функции является отрицательно полуопределенной на гиперплоскости p| rf(x) = 0.

Обратное, вообще говоря, неверно, но имеется близкий аналог.

Теорема 178:

Пусть множество X является открытым. Если функция f(·): X 7→R дважды дифференцируема и для всех x X и p Rn , таких что p 6= 0 и p| rf(x) = 0, выполнено p| r2f(x)p < 0, то

функция f(·) является квазивогнутой.

Другими словами, достаточным условием квазивогнутости дважды дифференцируемой функции является то, что ее матрица Гессе r2f(x) является отрицательно определенной на гиперплоскости p| rf(x) = 0 при всех x X , таких что rf(x) 6= 0, и отрицательно определенной при x X , таких что rf(x) = 0.