2.4. Представление предпочтений функцией полезности

24

2.3.1Задачи

/13. Какое наименьшее число вопросов требуется задать индивидууму с неоклассическими предпочтениями, чтобы выявить его предпочтения на потребительских наборах, состоящих из 5 благ, каждое из которых может потребляться в количестве 0 или 1?

/14. Пусть некто предложил в качестве аксиом строгого отношения предпочтения постулировать асимметричность и транзитивность. Какие проблемы на этом пути Вы видите?

/15. Пусть < — нестрогое отношение предпочтения (полное и транзитивное бинарное отношение), заданное на X , а (x y (x < y) и (y < x)) и (x y (x < y) и (y < x)) — строгое отношение предпочтения и отношение эквивалентности, построенные на его основе. Каким свойствам будут удовлетворять отношения и ?

/16. Пусть X = R+ , x y x > y, x < y x > y и x y x = y. Покажите, что тройка бинарных отношений h, <, i представляет собой неоклассические предпочтения.

Объясните, почему в многомерном случае (X = Rn+ при n > 2) нельзя ввести неоклассические предпочтения аналогичным образом.

/17. (Продолжение) Покажите, что для любых x, y X выполняется ровно одно из трех соотношений: x y, y x, x y.

/18. (Продолжение) Докажите, что для любых x, y, z X таких, что x < y и y z, выполнено x < z. Какие еще свойства, аналогичные этому, выполнены для данных предпочтений?

/19. (Продолжение) Докажите что при полноте отношения < определение строгого отношения предпочтения эквивалентно x y (y < x).

/20. Докажите недоказанные в основном тексте пункты Теоремы 4.

/21. Пусть h, <, i — неоклассические предпочтения. Рассмотрим семейство множеств (кривых) безразличия, построенных на основании . Как на основании порядка, задаваемого неоклассическими предпочтениями, корректно и непротиворечиво ввести порядок на этом семействе? Какими свойствами он обладает?

/22. Докажите Теорему 5.

/23. Изложите формально подход, основанный на «карте кривых безразличия», и продемонстрируйте его связь с неоклассическими предпочтениями.

/24. Покажите, что если нестрогое и строгое отношения предпочтения связаны соотношением x y (x < y, но не y < x),

то построенные на их основе правила выбора (см. Определение 6) совпадут, то есть

C (A) = C<(A) A A.

2.4Представление предпочтений функцией полезности

Вэтом параграфе мы рассмотрим условия, при выполнении которых можно получить числовой индикатор полезности — функцию полезности16 — с некоторыми наперед заданными

16

Понятие полезности (пользы) появилось впервые в работах английского философа Иеремии Бентама (1748-1832): «. . . стремиться к удовольствию и избегать страдания составляет его (человека) единственную задачу. . . Польза есть понятие отвлеченное. Оно выражает свойство или способность какого-нибудь предмета предохранить от какого-нибудь зла или доставить какое-нибудь благо.» (Цит. по Юм Д. Опыты.

2.4. Представление предпочтений функцией полезности

25

свойствами. Под функцией полезности потребителя традиционно понимается некоторая вещественнозначная функция, упорядочивающая альтернативы из множества допустимых альтернатив X таким же образом, как и предпочтения17. Функция полезности является удобным инструментом анализа выбора потребителя, особенно в приложениях теории. Например, с помощью нее удобно изучать вопросы сравнительной статики — как изменяется потребительский выбор при изменении параметров модели.

Определение 7:

Будем говорить, что функция u(·): X 7→R является функцией полезности, соответствующей предпочтениям h , <, i (другими словами, представляющей эти предпочтения), если для всякой пары потребительских наборов x, y X соотношение x < y выполнено тогда и только тогда, когда u(x) > u(y).

Замечание: Следует понимать, что если некоторые предпочтения могут быть представлены функцией полезности u(·), то данные предпочтения могут быть представлены также и суперпозицией f(u(·)), где f(·) — некоторая возрастающая функция (см. задачу 30). Т. е. при наличии хотя бы одной функции, представляющей предпочтения потребителя, мы автоматически имеем бесконечное множество функций полезности, таким же точно образом упорядочивающих потребительские наборы, и, соответственно, эквивалентных с точки зрения описания потребительских предпочтений. Некоторые из этого бесконечного множества функций полезности могут быть более удобными для анализа, чем другие, например, обладать такими свойствами как непрерывность, дифференцируемость, вогнутость, квазилинейность, сепарабельность

ит. п. (см. далее).

Всвязи с приведенным определением естественно возникает вопрос о том, какие свойства предпочтений (и множества альтернатив, на которых заданы предпочтения) гарантируют существование функции полезности, представляющей эти предпочтения. Вначале приведем утверждение, которое дает нам необходимое условие существования функции полезности.

Заметим, прежде всего, что Определение 7 намеренно сформулировано таким образом, чтобы учесть возможность того, что предпочтения не являются неоклассическими. Для самых «ходовых» случаев неполной рациональности (см. параграф 2.B) предпочтения можно описать, если задать нестрогое отношение предпочтения. При этом оно определяется как

"Бентам И. Принципы законодательства. О влиянии условий времени и места на законодательство. Руководство по политической экономии. М., 1895."

Бентам И. Принципы законодательства // Антология мировой политической мысли: в 5 т. TI – М., 1997 Бентам И. Введение в основания нравственности и законодательства. - М.: РОССПЭН, 1998. - 415 с. - (Ис-

тория полит. мысли).

И. Бентам Принципы законодательства. — О влиянии условий, времени и места на законодательство. — Руководство по политической экономии. Вып. 5. М, 1896) ??J. Bentham: An Introduction to the Principles of Morals and Legislation, London: T. Payne, 1789

17??Понятие функции полезности эволюционировало вместе с экономической теорией. Так Г. Госсен (см. сноску 4 на с. 66), впервые систематическим образом рассмотревший понятие функции полезности, предполагал, что она представляет собой сумму полиномов второй степени, причем все перекрестные произведения отсутствуют. Дальнейшее обобщение понятия полезности принадлежит Уильяму Стенли Джевонсу (W. S. Jevons: The Theory of Political Economy, London: Macmillan, 1871) предложившего в качестве функции полезности сумму произвольных вогнутых функций одного аргумента. Фрэ??нсис Ис??идро Эджворт (F. Y. Edgeworth:

Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences, London: C. Kegan Paul & Co., 1881) пошел дальше всех предыдущих авторов и в качестве функции полезности рассмотрел произвольную функцию многих переменных, без ограничения на смешанные производные. Следует отметить, что все эти авторы мыслили о функции полезности в рамках кардиналистского подхода. В дальнейшем развитие концепции полезности происходит в рамках ординалистского подхода, начала которого заложены в работах Вильфредо Парето (V. Pareto: Manuel d’´economie politique, Paris: V. Giard et E. Bri`ere, 1909). Подробнее об истории развития понятия полезности и теории потребителя см. H. S. Houthakker: The Present State of Consumption Theory, Econometrica 29 (1961): 704–740 и G. Stigler: The Development of Utility Theory, Journal of Political Economy 58 (1950): 307–327, 373–396.

2.4. Представление предпочтений функцией полезности

26

< = («лучше или безразлично»). Если для каждой пары наборов x, y X выполнено не более, чем одно из соотношений x y, x y, x y18, то, зная <, отношения иможно однозначно восстановить по следующим правилам:

x y, если x < y и		(y < x);	(P4)
x y, если x < y и y < x.			(P5)

В нижеприведенной теореме мы будем исходить именно из этих допущений.

Теорема 6:

Если существует функция полезности, представляющая предпочтения h, <, i, заданные на X , то эти предпочтения являются неоклассическими.

Доказательство: Поскольку отношение >, заданное на множестве определения функции полезности (подмножестве R), является полным и транзитивным, то отношение < на X тоже полно и транзитивно. Кроме того, очевидно, что (P5) совпадает с (P3), а (P4) при полноте < эквивалентно (P1). Таким образом, согласно пункту (ii) Теоремы 3 рассматриваемые предпочтения являются неоклассическими.

Как несложно понять, если предпочтения являются неоклассическими, то для того, чтобы проверить, представляет ли их данная функция u(·), достаточно проверить, что для всякой пары альтернатив x, y X соотношение x y верно тогда и только тогда, когда u(x) > u(y).

В дальнейшем в этой главе (за исключением задач и приложения, посвященного предпочтениям, отличным от неоклассических) мы будем рассматривать только неоклассические предпочтения и во многих случаях не будем оговаривать это особо, говоря просто «предпочтения».

Отметим, что когда множество альтернатив не более чем счетное (например, счетное), условие, что предпочтения являются неоклассическими, является достаточным для существования функции полезности. (Множество альтернатив будет счетным, например, когда все блага потребляются только в целых количествах.)

Теорема 7:

Если множество альтернатив X не более чем счетно, то для любых неоклассических предпочтений на X существует представляющая их функция полезности.

Доказательство: Поскольку множество альтернатив X не более чем счетно, то его можно представить в виде последовательности альтернатив xi , i = 1, 2, . . .. Доказательство утверждения строится в виде алгоритма.

Пусть мы уже присвоили величину полезности первым N альтернативам из данной последовательности. Требуется присвоить величину полезности альтернативе xN+1 . Рассмотрим два подмножества множества AN = {x1, . . . , xN }:

n o n o

AN+ = x AN x < xN+1 и AN− = x AN xN+1 < x .

Обозначим через x¯ такой элемент множества AN+ , что x < x¯ для всех x AN+ . В случае неединственности такого элемента берем любой из них. Аналогичным образом обозначим через x˜ такой элемент множества AN− , что x˜ < x для всех x AN− . Существование x¯ (при непустом множестве AN+ ) и x˜ (при непустом множестве AN− ) следует из полноты и транзитивности отношения <. Доказательство этого оставляется в качестве упражнения19.

Возможны 4 случая:

18Естественно предположить также, в качестве минимального требования рациональности, что нестрогое отношение предпочтения удовлетворяет условию рефлексивности (x < x).

19См. задачу 34. См. также Теорему 15.

2.4. Представление предпочтений функцией полезности

27

•AN+ = . Тогда можно взять u(xN+1) = u(x˜) + 1.

•AN− = . Тогда можно взять u(xN+1) = u(x¯) − 1.

•AN+ 6= , AN− 6= , AN+ ∩ AN− = . Тогда можно взять u(xN+1) = (u(x¯) + u(x˜))/2.

•AN+ 6= , AN− 6= , AN+ ∩ AN− 6= . В этом случае берем u(xN+1) = u(x), где x — произвольный элемент множества AN+ ∩ AN− (по построению все элементы множества AN+ ∩ AN− имеют одну и ту же полезность).

Чтобы закончить описание алгоритма, положим A1 = {x1} и u(x1) = 0. Заметим, что при таком построении функции полезности свойство

x < y u(x) > u(y)

выполнено для всех x, y AN при произвольном N (см. задачу 35). Поэтому построенная таким образом функция u(·) действительно является функцией полезности.

Если же множество альтернатив не является счетным, то утверждение в общем случае неверно. Это показывает, пример предпочтений на основе лексикографического упорядочения потребительских наборов из R2+ .

Пример 4:

Лексикографическое упорядочение называется так, поскольку оно ранжирует наборы подобно правилу расположения слов в словаре. В двумерном случае (X = R2+ ) чем больше первого блага, тем лучше набор, а если количество первого блага в двух наборах одинаково, то имеет значение количество второго блага. Таким образом, согласно этому упорядочению x лучше y (x L y), если x1 > y1 или же если x1 = y1 и x2 > y2 . Таким образом заданное упорядочение L удовлетворяет свойствам асимметричности и отрицательной транзитивности. Однако соответствующие неоклассические предпочтения не представляются никаким численным индикатором полезности. Докажем это.

Предположим противное. Пусть существует соответствующая этим предпочтениям функция полезности, т. е. функция (принимающая действительные значения), такая что

x L y uL(x1, x2) > uL(y1, y2).

Сопоставим каждому неотрицательному действительному числу x1 некоторое рациональное число r(x1), такое что uL(x1, 2) > r(x1) > uL(x1, 1). Такое r(x1) найдется, поскольку множество рациональных чисел всюду плотно в множестве действительных чисел.

Если x1, x01 > 0 — два числа, таких что x1 > x01 , то по определению лексикографического упорядочения имеем uL(x1, 1) > uL(x01, 2). Кроме того, uL(x1, 2) > r(x1) > uL(x1, 1) и uL(x01, 2) > r(x01) > uL(x01, 1). В силу этих соотношений имеем

r(x1) > uL(x1, 1) > uL(x01, 2) > r(x01).

Тем самым, из того, что x1 > x01 имеем, что r(x1) > r(x01). В силу этого r(·) является взаимнооднозначной функцией. Область определения этой функции — неотрицательные действительные числа (это множество является континуумом), а область значения — некоторое подмножество множества рациональных чисел (т. е. счетное множество). Подобное невозможно, так как невозможно построить взаимнооднозначное соответствие между счетным множеством и континуумом. Таким образом, мы пришли к противоречию, и, тем самым, доказали, что не существует функции полезности, соответствующей лексикографическому упорядочению. 4

Отметим, что, однако, существует ряд случаев, для которых можно гарантировать существование функции полезности, даже если множество альтернатив не является конечным или счетным. Так, например, Жерар Дебре20 доказал, что функция полезности существует, если

20G. Debreu: Representation of a Preference Ordering by a Numerical Function, in Decision Processes, R. M. Thrall et al. (ed.), New York: John Wiley & Sons, 1954.

2.4. Представление предпочтений функцией полезности

28

предпочтения непрерывны. Существует несколько эквивалентных определений непрерывности. Мы дадим одно из таких определений, а затем укажем другие возможные определения.

Определение 8:

Неоклассические предпочтения h, <, i на X Rl , называются непрерывными, если для любых сходящихся последовательностей допустимых наборов {xn}, {yn} (xn, yn X ), таких что xn < yn при всех n, пределы которых x = limn→∞ xn и y = limn→∞ yn являются допустимыми наборами (x, y X ), выполнено x < y.

Следующая теорема указывает некоторые альтернативные определения непрерывности21

Теорема 8:

Пусть h, <, i — неоклассические предпочтения на X Rl . Тогда следующие утверждения эквивалентны:

(1) предпочтения непрерывны в смысле Определения 8;

(2) для любого x X как множество L+(x) = { y X x < y }, так и множество L−(x) =

{ y X x 4 y } замкнуто (в Rl ).

(3)если x y (x, y X ), то существуют ε-окрестности Vx и Vy точек x и y соответ-

ственно, такие что для любых x0 Vx ∩ X и y0 Vy ∩ X выполнено x0 y0 .

Доказательство: Доказательство проведем по схеме 1 2 3 1.

(1)(2) Возьмем произвольный набор x X и любую сходящуюся последовательность

{yn}, целиком лежащую в L+(x). Пусть y — предел этой последовательности22. По определению L+(x) для любого n выполнено x < yn . Поскольку предпочтения непрерывны, отсюда следует, что x < y, т. е. y L+(x). Замкнутость второго множества доказывается аналогично.

(2)(3) Прежде всего, заметим, что множество L+(x) замкнуто тогда, и только тогда, когда его дополнение в Rl , множество Rl\L+(x), открыто. Аналогично, L−(x) замкнуто тогда,

итолько тогда, когда Rl\L−(x) открыто.

Пусть x y. Рассмотрим два возможных случая.

(a)Существует набор z X , такой что x z y. Тогда x лежит в открытом множестве Rl\L−(z) и поэтому существует ε-окрестность этого набора, Vx , целиком лежащая в Rl\L−(z). Аналогично, y лежит в Rl\L+(z) вместе с некоторой окрестностью Vy .

(b)Не существует набора z X такого, что x z y. Набор x лежит в Rl\L−(y) вместе

снекоторой окрестностью Vx , а y лежит в Rl\L+(x) вместе с некоторой окрестностью Vy . Читателю предлагается самостоятельно проверить, что в каждом из случаев (a), (b) для

любых x0 Vx ∩ X и y0 Vy ∩ X выполнено x0 y0 (см. задачу 41).

21Мы исходим, из того, что X является подмножеством Rl . Однако приведенные альтернативные определения, фактически, являются более общими и могут быть применены с определенными поправками к множествам допустимых потребительских наборов другой природы. Поправки состоят в том, чтобы рассматривать все относительно X (как если бы точек вне X не существовало):

•для любого x X как множество L+(x), так и множество L−(x) замкнуто в X (аналог определения

(2) из Теоремы 8);

• для любого x X как множество L++(x) = { y X x y }, так и множество L--(x) = { y X x y } открыто в X (очевидная переформулировка предыдущего определения);

• множество открыто в X × X (аналог определения (3) из Теоремы 8);

•множество < замкнуто в X × X (очевидная переформулировка предыдущего определения и аналог исходного определения непрерывности).

Соответственно, приведенное доказательство эквивалентности определений подходит практически без изменений.

22Как обычно, предполагается, что X замкнуто и поэтому y X .

2.4. Представление предпочтений функцией полезности

29

(3) (1) Возьмем некоторые сходящиеся последовательности допустимых наборов {xn},

{yn}, такие что xn < yn n. Если бы y x, где x = limn→∞ xn , y = limn→∞ yn , тогда для точек x, y нашлись бы окрестности Vx и Vy , такие что для любых допустимых наборов

x0 Vx и y0 Vy выполнено y0 x0 . Это означает, что при достаточно больших значениях n имеем yn xn , что противоречит xn < yn . Таким образом, получили, что x < y.

Приведенные эквивалентные определения непрерывности позволяют выявить содержательный смысл понятия непрерывности: если мы явно предпочитаем один из наборов другому, то при рассмотрении достаточно близких наборов наша ранжировка сохранится. Кроме того, согласно этой теореме непрерывность предпочтений можно переформулировать как требование замкнутости верхнего и нижнего лебеговских множеств23.

Пример 5 (продолжение Примера 4):

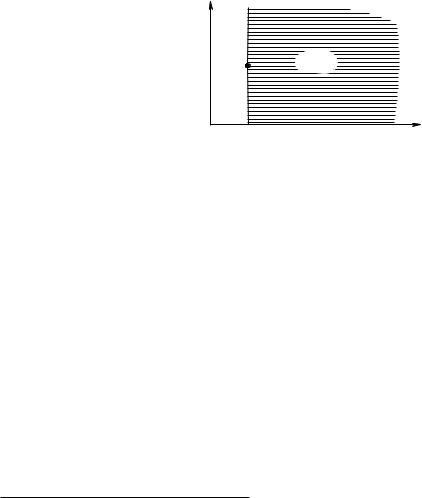
В случае лексикографических предпочтений на R2+ для любого x R2+ множества L+(x) и L−(x) не являются ни замкнутыми, ни открытыми. Здесь <L задается на основе L обычным образом. Несложно увидеть, что

x <L y ((x1 > y1) или (x1 = y1 и x2 > y2)).

x2
x	L+(x)
	x1

Рис. 2.2. Верхнее лебеговское множество для лексикографического упорядочения

Рис. 2.2 показывает одно из верхних лебеговских множеств для лексикографических предпочтений. Очевидно, что изображенное на рисунке множество L+(x) не является ни замкнутым, ни открытым, и, таким образом, лексикографические предпочтения не являются непре-

рывными. (То же самое имеет место и для L−(x).)

4

Теперь сформулируем и частично докажем анонсированную выше теорему Ж. Дебре о существовании функции полезности, представляющей неоклассические предпочтения.

Теорема 9:

Для любых непрерывных неоклассических предпочтений на X Rl существует представляющая их непрерывная функция полезности.

Доказательство: Как уже говорилось, мы не будем полностью доказывать этот результат. Докажем только часть его, а именно, существование функции полезности. За доказательством непрерывности заинтересованный читатель отсылается к оригинальной работе Траута Радера24, чей вариант доказательства теоремы Дебре мы здесь приводим.

Рассмотрим систему шаров в Rl с рациональными центрами и радиусами. Очевидно, что таких шаров счетное число. На основании этих шаров построим систему множеств {On}+n=1∞

23Иногда, свойство замкнутости верхнего (нижнего) лебеговского множества называют полунепрерывностью предпочтений сверху (снизу).

24На самом деле, построенная функция полезности не будет непрерывной. Чтобы получить непрерывную функцию, требуется еще «склеить» разрывы. См. J. T. Rader: The Existence of a Utility Function to Represent Preferences, Review of Economic Studies 30 (1963): 229–232.

2.4. Представление предпочтений функцией полезности

30

по следующему принципу: в эту систему попадают непустые пересечения исходной системы шаров с множеством X . Обозначим через L--(x) множество потребительских наборов из X , которые строго хуже x, т. е. L--(x) = { y X | x y }. Введем в рассмотрение множество индексов тех множеств On , все точки которых хуже x: N(x) = { n | On L--(x) }.

Покажем, что Sn N(x) On = L--(x). Включение Sn N(x) On L--(x) очевидно, так как для каждого n N(x) выполнено On L--(x).

Докажем обратное включение L--(x) Sn N(x) On . Возьмем некоторую точку y L--(x). Множество Rl\L+(x) открыто (так как L+(x) замкнуто), и ему принадлежит точка y (так как L--(x) Rl\L+(x)). В это множество можно вписать шар с рациональными центром и радиусом, содержащий точку y. Другими словами, существует множество On , которое содержит y. Следовательно, y Sn N(x) On .

Далее, каждой точке x X сопоставим величину

X 1 u(x) = n N(x) 2n .

В случае, когда N(x) = , положим u(x) = 0.

Покажем, что определенная таким образом функция u(·) представляет рассматриваемые предпочтения.

Пусть x < y. Тогда L--(y) L--(x), откуда N(y) N(x) и, следовательно, u(x) > u(y). Пусть теперь u(x) > u(y). Предположим, что x < y не выполняется, т. е. y x. В этом

случае L--(x) L--(y), и при этом L--(x) 6= L--(y). Отсюда заключаем, что N(x) N(y) и N(x) 6= N(y), а значит, по определению u(·), имеем u(x) < u(y). Получили противоречие с u(x) > u(y). Таким образом, доказано, что u(x) > u(y) влечет x < y. Тем самым, построенная

функция u(·), является функцией полезности для исходных предпочтений.
x2

L+i (x)

x1

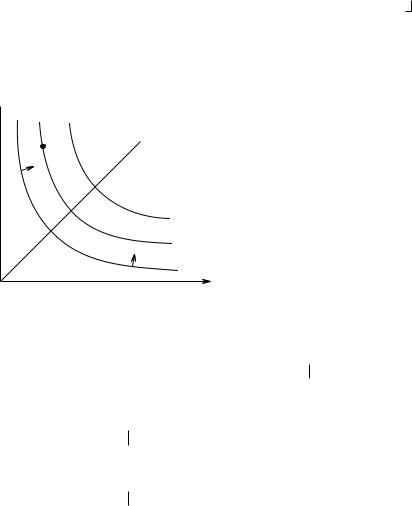
Рис. 2.3. Построение функции полезности по схеме Радера.

Данный вариант доказательства имеет достаточно ясную графическую интерпретацию (см. Рис. 2.3). Мы заполняем нижнее лебеговское множество «шариками» с рациональными радиусами и центрами, и берем в качестве функции полезности основанный на этих «шариках» измеритель размера нижнего лебеговского множества.

Еще одно элегантное доказательство теоремы Дебре с выразительной графической интерпретацией можно построить при довольно естественном предположении о монотонности предпочтений.

Достаточно разумно потребовать, чтобы полезность индивидуума возрастала при росте количества потребляемых благ, т. е. потребитель предпочитал большее количество блага меньшему.

2.4. Представление предпочтений функцией полезности

31

Определение 9:

Предпочтения на X называются монотонными, если x, y X из x > y следует x < y.

Определение 10:

Предпочтения называются строго монотонными, если из x > y и x 6= y следует x y.

Докажем ослабленный вариант теоремы Дебре, предполагая строгую монотонность.

Теорема 10:

Для любых непрерывных, строго монотонных предпочтений на X = Rl+ существует представляющая их непрерывная, строго монотонная функция полезности.

Доказательство: Требуемую функцию полезности найдем, сопоставив каждому x Rl+ такое число u(x), что x u(x)1l, где 1l — l-мерный вектор, состоящий из единиц. (Рис. 2.4 иллюстрирует идею доказательства.)

x2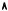

x

u(x)1l

x1

Рис. 2.4. Построение функции полезности при предположении монотонности предпочтений

Покажем, что такое число u(x) всегда существует и единственно. Для этого мы должны найти для каждого набора x эквивалентный ему набор из множества U = { u1l u R+ }, которое является лучом, выходящим из начала координат. Сопоставим рассматриваемому набору x множество чисел, соответствующих не худшим наборам из U :

U+(x) = { u R+ u1l < x } ,

и множество чисел, соответствующих не лучшим наборам из U :

U−(x) = { u R+ x < u1l } .

Эти множества не пусты, так как из свойства строгой монотонности следует, что 0 U−(x) и maxk{xk} U+(x).

Множество U+(x) лежит выше U−(x), поскольку из строгой монотонности следует, чтоu1 U−(x) и u2 U+(x) выполнено u1 6 u2 .

Обозначим u+ = inf U+(x) и u− = sup U−(x). Эти величины конечны, так как множества U−(x) и U+(x) ограничены сверху и снизу соответственно. По непрерывности предпочтений u+ U+(x) и u− U−(x). При этом u+ > u− . Покажем, что u+ = u− . Пусть это не так. Тогда существует число u0 такое, что u− < u0 < u+ . При этом u0 / U−(x) и u0 / U+(x). Это невозможно, так как по свойству полноты нестрогого отношения предпочтения мы должны иметь либо u01l < x, либо u01l 4 x.

Полученная точка u = u+ = u− удовлетворяет требуемому условию x u1l и единственна. Заданная таким образом функция u(x) является функцией полезности. Пусть x1 < x2 .

По построению x1 u(x1)1l и x2 u(x2)1l. Значит, x1 < x2 тогда и только тогда, когда